Quadratic Inequalities - Definition, Expression, Graphs, Solved Examples

Inequalities are mathematical expressions showing the relationship between two values, indicating that one value is greater than, less than, or not equal to another. Understanding inequalities is crucial for solving various mathematical problems, from basic arithmetic to advanced calculus. Quadratic inequalities are specially used for a parabola that is two-degree curves.

This Story also Contains

1. Quadratic Inequalities
2. What Do You Mean By Quadratic Inequalities?
3. Definition
4. Standard Form
5. Solving Quadratic Inequalities
6. Notations Used In Quadratic Inequalities
7. Method to solve quadratic inequalities
8. Properties
9. Solved Examples Based On Quadratic Inequalities

In this article, we will cover the concept of the sign of quadratic expression. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

Quadratic Inequalities

Quadratic inequalities can be derived from quadratic equations. The word "quadratic" comes from the word "quadrature", which means "square" in Latin. The general form of a quadratic equation is $a x^2+b x+$ $c=0$. Further if the quadratic polynomial $a x^2+b x+c$ is not equal to zero, then they are either $a x^2+b x+c$ $>0$, or $a x^2+b x+c<0$, and are referred as quadratic inequalities.

What Do You Mean By Quadratic Inequalities?

The quadratic inequality is a second-degree expression in x and has a greater than (>) or lesser than (<) inequality. the quadratic inequality has been derived from the quadratic equation $a x^2+b x+c=0$.

Definition

If a quadratic polynomial in one variable is less than or greater than some number or any other polynomial (with a degree less than or equal to 2), then it is said to be a quadratic inequality. The difference between a quadratic equation and a quadratic inequality is that the quadratic equation is equal to some number while quadratic inequality is either less than or greater than some number. Some examples are:

• $\mathrm{x}^2+\mathrm{x}-1>0$
• $2 x^2-5 x-2 \geq 0$

Standard Form

The standard form of quadratic inequalities in one variable is almost the same as the standard form of a quadratic equation. The only difference is that the quadratic equation has an "equal to" sign in it while a quadratic inequality has a "greater than" or "less than" sign (> or <). The standard form of quadratic inequality can be represented as:

Solving Quadratic Inequalities

If $a x^2+b x+c>0$ and $(a \neq 0)$ :
Case 1: (i) If $D\left(b^2-4 a c\right)>0$, i.e., then $f(x)$ has two different roots and $a<b$.
If $a>0$, then

$
x \in(-\infty, \alpha) \cup(\eta, \infty)
$

And, if $a<0$, then, $x \in(\alpha, \beta)$
Case 2: If $D\left(b^2-4 a c\right)=0$, i.e., the quadratic equation $f(x)$ has equal roots, i.e., $a=b$.
If $a>0$, then,

$
x \in(-\infty, \alpha) \cup(\alpha, \infty)
$

And, if $a<0$, then $x \in \varnothing$
Case 3: If $D\left(b^2-4 a c\right)<0$, i.e., the quadratic equation has imaginary roots.
If $a>0$, then

$
x \in R
$

And, if $a<0$ then, $x \in \varnothing$
In general, if $(x-a)(x-b) \geq 0$, then $a \leq x \leq b$,
$(\mathrm{x}-\mathrm{a})(\mathrm{x}-\mathrm{b}) \leq 0$ and $\mathrm{a}<\mathrm{b}$, then $\mathrm{a} \leq \mathrm{x}$ or $\mathrm{x} \geq \mathrm{b}$.

Notations Used In Quadratic Inequalities

The notation of greater than (>) and lesser. than (< ) is often used in quadratic equation.

• ( ) → Open Brackets
• [ ] → Closed Brackets
• o → Open Value( x cannot take this value)
• • → Closed Value( x can take this value)
• (-1, 1) → x cannot take value -1 and 1.
• [-1, 1) → x can take value -1 but not 1.
• (-1, 1] → x cannot take value -1 but it can take value 1.
• [-1, 1] → x can take both -1 and 1 values

Method to solve quadratic inequalities

The wavy curve method is used to solve the inequality of the type. Inequalities can be solved by drawing their graph and before that converting them into standard form with zero at right hand side. Then drawing the graph accordingly with area above x axis bankor below

$
\frac{\mathrm{f}(\mathrm{x})}{\mathrm{g}(\mathrm{x})}>0 \text { or }(<, \leq, \geq)
$

We use the following steps in the wavy curve method to solve a question (start by getting 0 on one side of inequality)
1: Factorize the numerator and denominator into linear factors.
2: Make coefficients of $x$ positive in all linear factors.
3: Equate each linear factor to zero and find the values of $x$ in each case. The values are called critical points. Do not include the linear factors with even power while finding critical points.
4: Identify distinct critical points on the real number line. The " $n$ " numbers of distinct critical points divide real number lines in ( $n+1$ ) sub-intervals.
5: The sign of rational function in the rightmost interval is positive. Alternate sign in adjoining intervals on the left.
6. Check for each critical point and point from even powered linear factors, if these are to be included in the answer or not.

For Example: using the wavy curve method to find the interval of $x$ for the inequality given :

$
\frac{x}{x-1} \geq 0
$

Steps
- 0 on the right-hand side (already there)
- all linear factors (already present)
- Critical points are: $x=0,1$

The critical points are marked on the real number line. Starting with a positive sign in the rightmost interval, we denote signs of adjacent intervals by alternating signs.

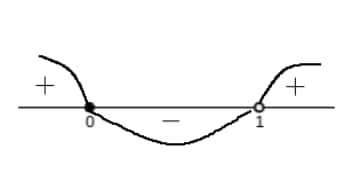
Hence, $x \in(-\infty, 0] \cup(1, \infty)$
Note that 1 cannot be taken in the answer as at $x=1$, the denominator becomes 0 , and hence expression is not defined.

Properties

(a) In an inequality, any number can be added or subtracted from both sides of the inequality.

(b) Terms can be shifted from one side to the other side of the inequality. The sign of inequality does not change.

(c) If we multiply both sides of the inequality by a non-zero positive number, then the sign of inequality does not change.

(d) In the inequality, if the sign of an expression is not known, then it cannot be cross-multiplied. Similarly, without knowing the sign of an expression, a division is not possible.

Recommended Video Based on Quadratic Inequalities

Solved Examples Based On Quadratic Inequalities

Example 1: The least value of $|z|_{\text {where } \mathbf{z}}$ is a complex number that satisfies the inequality $\exp \left(\frac{(|z|+3)(|z|-1)}{|| z|-1|} \log _e 2\right) \geqslant \log _{\sqrt{2}}|5 \sqrt{7}+9 i|, i=\sqrt{-1}$,is equal to:
Solution:

$
\begin{aligned}
& \exp \left(\frac{(|z|+3)(|z|-1)}{|| z|+1|} \ln 2\right) \geq \log _{\sqrt{2}}|5 \sqrt{7}+9 i| \\
& \Rightarrow 2^{\frac{(|z|+3)(|z|-1)}{(\mid z+1)} \geq \log _{\sqrt{2}}(16)} \\
& \Rightarrow 2^{\frac{(|z|+3)(|z|-1)}{(z \mid+1)} \geq 2^3} \\
& \Rightarrow \frac{(|z|+3)(|z|-1)}{(z \mid+1)} \geq 3 \\
& \Rightarrow(|z|+3)(|z|-1) \geq 3(|z|+1) \\
& |z|^2+2|z|-3 \geq 3|z|+3
\end{aligned}
$
$
\begin{aligned}
& \Rightarrow|z|^2+|z|-6 \geq 0 \\
& \Rightarrow(|z|-3)(|z|+2) \geq 0 \Rightarrow|z|-3 \geq 0 \\
& \Rightarrow|z| \geq 3 \quad \Rightarrow|z|_{\min }=3
\end{aligned}
$

Hence, the answer is 3.

Example 2: The integer ' k ', for which the inequality $x^2-2(3 k-1) x+8 k^2-7>0$ is valid for every real value of x , is
Solution:
The condition for a quadratic expression to be always positive is
a (coefficient of $x^2$ ) $>0$ and $D<0$
Now,
Coefficient of $x^2=1(>0)$
So, we have to apply only $\mathrm{D}<0$

$
\begin{aligned}
& \Rightarrow 4(3 \mathrm{~K}-1)^2-4 \times 1 \times\left(8 \mathrm{~K}^2-7\right)<0 \\
& \Rightarrow 9 \mathrm{~K}^2-6 \mathrm{~K}+1-8 \mathrm{~K}^2+7<0 \\
& \Rightarrow \mathrm{K}^2-6 \mathrm{~K}+8<0 \\
& \Rightarrow(\mathrm{K}-4)(\mathrm{K}-2)<0 \\
& \Rightarrow \mathrm{K} \in(2,4)
\end{aligned}
$

So, only one integer in this interval: $\mathrm{K}=3$.
Hence, the answer is 3 .

Example 3: The solution of $(x+1)(x-9)<0$ is
1) $[-\infty,-1] \cup(9-\infty)$
2) $(-\infty,-9) \cup(1, \infty)$
3) $[-1,9]$
4) $(-1,9)$

Solution:

$
(x+1)(x-9)<0
$

As the inequation is in standard form, we can make the sign scheme.
Roots: $-1,9$

So, the solution is (-1,9)

Example 4: Solution of $x(x-4)(x+5)>0$
1) $(-5,0) \cup(4, \infty)$
2) $(-\infty,-5) \cup(4, \infty)$
3) $(-5, \infty)$
4) None of these

Solution:
Already in standard form
Roots $x=0,4,-5$
Sign scheme

So, $(-5,0) \cup(4, \infty)$
Example 5: The solution of $\frac{x^3(x-4)(x+3)^2}{(x+1)} \geqslant 0$ is
1) $(-1,0] \cup[4, \infty)$
2) $(-1,0] \cup[4, \infty) \cup-3$
3) $(-1,0) \cup(4, \infty)$
4) $(-\infty,-3] \cup(-1,0] \cup[4, \infty)$

Solution:
Standard form
Roots: $x=0,4,-3$
Roots of denominator: -1
Sign scheme

Positive for $(-1,0) \cup(4, \infty)$
Zero for $0,4,-3$
So, the solution is $(-1,0] \cup[4, \infty) \cup-3$
Frequently Asked Questions(FAQ)-
1. What is inequalities?

Ans: Inequalities are the relationship between two expressions which are not equal to one another.
2. Solve $-5(x-1) \leq 10(2 x-3)$

Ans:

$
\begin{aligned}
& -5(x-1) \leqslant 010(2 x-3) \\
\Rightarrow \quad & (x-1) \geqslant \frac{10}{-5}(2 x-3) \\
\Rightarrow & x-1 \geqslant-2(2 x-3) \\
\Rightarrow & x-1 \geqslant-4 x+6 \\
\Rightarrow & x+4 x \geqslant 6+1 \\
\Rightarrow & 5 x \geqslant 7 \\
\Rightarrow & x \geqslant \frac{7}{5} \\
& \frac{-1}{2}<x \leq 3, \text { then } \frac{1}{x}
\end{aligned}
$

Ans:

$
\begin{aligned}
& -\frac{1}{2}<x \leqslant 3\left(-\frac{1}{2}<0,3>0\right) \\
& \Rightarrow-\frac{1}{2}<x<0^{-} \text {or } 0^{+}<x \leqslant 3 \\
& \Rightarrow-2>\frac{1}{x}>-\infty \text { or } \infty>\frac{1}{x} \geqslant \frac{1}{3} \\
& \Rightarrow \frac{1}{x} \in(-\infty,-2) \cup\left[\frac{1}{3}, \infty\right)
\end{aligned}
$

4. What is the solution of the expression $x^2<9$ ?

Ans: $x^2<9 \Rightarrow x^2-9<0 \Rightarrow(x-3)(x+3)<0$

$
x \in(-3,3)
$

5. The equation $e^{4 \mathrm{x}}+8 \mathrm{e}^{3 \mathrm{x}}+13 \mathrm{e}^{2 \mathrm{x}}-8 \mathrm{e}^{\mathrm{x}}+1=0, \mathrm{x} \in \mathbb{R}_{\text {has }}$ :

Ans: 1

$
\mathrm{e}^{4 x}+8 \mathrm{e}^{3 x}+13 \mathrm{e}^{2 x}+13 \mathrm{e}^{2 x}-8 \mathrm{e}^{\mathrm{x}}+1=0, x \in R
$

Let $\mathrm{e}^{\mathrm{x}}=\mathrm{t}>0 \& \mathrm{x}=\ln t$

$
t^4+8 t^3+13 t^2-8 t+1=0
$

Dividing by $\mathrm{t}^2$,

$\begin{aligned} & t^2+8 t+13-\frac{8}{t}+\frac{1}{t^2}=0 \\ & t^2+\frac{1}{t^2}+8\left(t-\frac{1}{t}\right)+13=0 \\ & \quad \mathrm{t}-\frac{1}{\mathrm{t}}=\mathrm{u} \Rightarrow \mathrm{t}^2+\frac{1}{t^2}-2 \mathrm{u}^2 \\ & \text { Let } \\ & \Rightarrow \mathrm{t}^2+\frac{1}{\mathrm{t}^2}=\mathrm{u}^2+2 \\ & \mathrm{u}^2+2+8 \mathrm{u}+13=0 \\ & (\mathrm{u}+3)(\mathrm{u}+5)=0 \\ & \mathrm{u}=-3 \& \mathrm{u}=-5 \\ & \mathrm{t}-\frac{1}{\mathrm{t}}=-3 \\ & \mathrm{t}^2+3 \mathrm{t}-1=0 \quad \mathrm{t}-\frac{1}{\mathrm{t}}=-5 \\ & \mathrm{t}^2+5 \mathrm{t}-1=0\end{aligned}$

$
\begin{aligned}
& 0<\alpha_1<1 \quad 0<\alpha_2<1 \\
& \Rightarrow \mathrm{x}_1=\ln \alpha_1<0 \quad \Rightarrow \mathrm{x}_2=\ln \alpha_2<0
\end{aligned}
$