Reduction Formulas For Integration by Parts With Solved Examples

Integration by Reduction is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These integration concepts have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

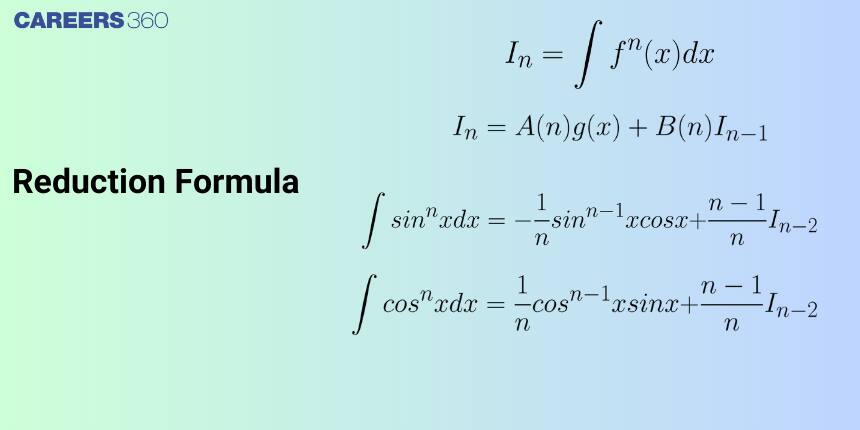
In this article, we will cover the concept of Integration by Reduction. This concept falls under the broader category of Calculus, a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), four questions have been asked on this concept, including one in 2020, one in 2021, and two in 2022. Over the last ten years of the JEE Main exam (from 2013 to 2023), two questions have been asked on this concept, including one in 2021, and one in 2023.

Reduction Formula

A reduction formula is the integration of the power of a function in terms of the integration of the lower power of the same function. By iteratively applying this formula, one can reduce a complicated integral into simpler forms, eventually leading to a basic integral that can be easily evaluated.

Derivation of a Reduction Formula

Proof for the integration of $\int x^n e^x$.

1. Integration by Parts:

Using the integration by parts formula, $d u \int u d v=u v-\int v$,

where: $u=x^n \quad$ and $\quad d v=e^x d x$

Therefore, $d u=n x^{n-1} d x$ and $v=e^x$

: $\int x^n e^x d x=x^n e^x-\int n x^{n-1} e^x d x$

(a) $\int \sin ^{\mathrm{n}} \mathrm{xdx}$

Let $\quad I_n=\int \sin ^n x d x=\int \sin ^{n-1} x \sin x d x$
take $\sin ^{\mathrm{n}-1} \mathrm{x}$ as first function and $\sin \mathrm{x}$ as second function

$
\begin{aligned}
& =-\sin ^{n-1} x \cos x+\int(n-1) \sin ^{n-2} x \cos ^2 x d x \\
& =-\sin ^{n-1} x \cos x+(n-1) \int \sin ^{n-2} x\left(1-\sin ^2 x\right) d x \\
& =-\sin ^{n-1} x \cos x+(n-1) \int\left(\sin ^{n-2} x-\sin ^n x\right) d x \\
& =-\sin ^{n-1} x \cos x+(n-1) I_{n-2}-(n-1) I_n \\
\therefore \quad n I_n & =-\sin ^{n-1} x \cos x+(n-1) I_{n-2} \\
\Rightarrow \quad I_n & =-\frac{\sin ^{n-1} x \cos x}{n}+\frac{n-1}{n} I_{n-2}
\end{aligned}
$
Thus, $\int \sin ^n x d x=\frac{-\sin ^{n-1} x \cos x}{n}+\frac{n-1}{n} \int \sin ^{n-2} x d x$

(b) $\int \tan ^n x d x$
$
\begin{aligned}
\text { Let } \quad I_n & =\int \tan ^n x d x \\
\Rightarrow \quad I_n & =\int \tan ^{n-2} x \tan ^2 x d x=\int \tan ^{n-2} x\left(\sec ^2 x-1\right) d x \\
& =\int \tan ^{n-2} x \sec ^2 x-I_{n-2}=\int t^{n-2} d t-I_{n-2}
\end{aligned}
$

where, $\tan x=t \Rightarrow \sec ^2 x d x=d t$

$\begin{aligned} & I_n=\frac{t^{n-1}}{n-1}-I_{n-2} \\ \therefore & I_n=\frac{\tan ^{n-1} x}{n-1}-I_{n-2} \\ \Rightarrow \quad & \int \tan ^n x d x=\frac{\tan ^{n-1} x}{n-1}-\int \tan ^{n-2} x d x\end{aligned}$

Integration of trigonometric function of power m for $m=4$.

$\therefore \int \tan ^4 x d x=\int \tan ^2 x \cdot \tan ^2 x d x=\int\left(\sec ^2 x-1\right) \tan ^2 x d x$Use $\sin ^4 x=\left(\sin ^2 x\right)^2=\left(\frac{1-\cos 2 x}{2}\right)^2, \cos ^4 x=\left(\cos ^2 x\right)^2=\left(\frac{1+\cos 2 x}{2}\right)^2$

(c) $\int \cos ^{\mathrm{n}} \mathrm{x} \mathrm{dx}$

Let $I_n=\int \cos ^n x d x=\int \cos ^{n-1} x \cos x d x$
Take $\cos ^{n-1} x$ as first function and $\cos x$ as second function.

$
\begin{aligned}
& =\cos ^{n-1} x \sin x+\int(n-1) \cos ^{n-2} x \sin ^2 x d x \\
& =\cos ^{n-1} x \sin x+(n-1) \int \cos ^{n-2} x\left(1-\cos ^2 x\right) d x \\
& =\cos ^{n-1} x \sin x+(n-1) I_{n-2}-(n-1) I_n \\
\therefore n I_n & =\cos ^{n-1} x \sin x+(n-1) I_{n-2} \\
\text { or } \int & \cos ^n x d x=\frac{\cos ^{n-1} x \sin x}{n}+\frac{n-1}{n} \int \cos ^{n-2} x d x
\end{aligned}
$

(d) $\int \cot ^n \mathrm{x} \mathrm{dx}$

Let $I_n=\int \cot ^n x d x=\int \cot ^{n-2} x \cot ^2 x d x$

$
\begin{aligned}
& =\int \cot ^{n-2} x\left(\csc ^2 x-1\right) d x \\
& =\int \cot ^{n-2} x \csc ^2 x d x-I_{n-2} \\
& =\int t^{n-2} d t-I_{n-2}
\end{aligned}
$

where, $\cot x=t \Rightarrow \csc ^2 x d x=-d t$

$
\begin{aligned}
I_n & =-\frac{\cot ^{n-1} x}{n-1}-I_{n-2} \\
\therefore \quad \int \cot ^n x d x & =-\frac{\cot ^{n-1} x}{n-1}-\int \cot ^{n-2} x d x
\end{aligned}
$

(e) $\int \sec ^{\mathrm{n}} \mathrm{xdx}$

Let $I_n=\int \sec ^n x d x=\int \sec ^{n-2} x \sec ^2 x d x$
Take $\sec ^{\mathrm{n}-2} \mathrm{x}$ as first function and $\sec ^2 \mathrm{x}$ as a second function

$
\begin{aligned}
& \quad=\sec ^{n-2} x \tan x-\int(n-2) \sec ^{n-3} x \sec x \tan x \cdot \tan x d x \\
& \quad=\sec ^{n-2} x \tan x-(n-2) \int \sec ^{n-2} x\left(\sec ^2 x-1\right) d x \\
& \quad=\sec ^{n-2} x \tan x-(n-2) I_n+(n-2) I_{n-2} \\
& \Rightarrow(n-1) I_n=\sec ^{n-2} x \tan x+(n-2) I_{n-2} \\
& \text { or } \quad I_n=\frac{\sec ^{n-2} x \tan x}{(n-1)}+\frac{(n-2)}{(n-1)} I_{n-2} \\
& \therefore \int \sec ^n x d x=\frac{\sec ^{n-2} x \tan x}{(n-1)}+\frac{(n-2)}{(n-1)} \int \sec ^{n-2} x d x
\end{aligned}
$

(f) $\int \csc ^{\mathrm{n}} \mathrm{x} d \mathrm{x}$
$
\begin{aligned}
& \text { Let } I_n=\int \csc ^n x d x=\int \csc ^{n-2} x \csc ^2 x d x \\
& =\csc ^{n-2} x(-\cot x)-\int(n-2) \csc ^{n-2} x\left(\csc ^2 x-1\right) d x \\
& =-\csc ^{n-2} x(-\cot x)-(n-2) \int\left(\csc ^n x-\csc ^{n-2} x\right) d x \\
& =-\csc ^{n-2} x \cot x-(n-2) I_n+(n-2) I_{n-2} \\
& \therefore \quad(n-1) I_n=-\csc ^{n-2} x \cot x+(n-2) I_{n-2} \\
& \text { or } \quad I_n=-\frac{\csc ^{n-2} x \cot x}{n-1}+\frac{n-2}{n-1} I_{n-2} \\
& \therefore \int \csc ^n x d x=-\frac{\csc ^{n-2} x \cot x}{n-1}+\frac{n-2}{n-1} \int \csc ^{n-2} x d x
\end{aligned}
$

Integration of the type $\int \cos ^{\mathrm{m}} \mathrm{x} \sin \mathrm{nx} \mathrm{dx}$

Let $\mathrm{I}_{\mathrm{m}, \mathrm{n}}=\int \cos ^{\mathrm{m}} \mathrm{x} \sin \mathrm{nx} \mathrm{dx}$
To evaluate this integral, we will use integration by parts method Here, take $\cos ^{\mathrm{m}} \mathrm{x}$ as the first function and $\sin \mathrm{nx}$ as the second function.

$
\begin{aligned}
& =-\frac{\cos ^m x \cos n x}{n}-\frac{m}{n} \int \cos ^{m-1} x \sin x \cos n x d x \\
& =-\frac{\cos ^m x \cos n x}{n}-\frac{m}{n} \int \cos ^{m-1} x\{\sin n x \cos x-\sin (n-1) x\} d x \\
& \text { [using } \sin (n-1) x=\sin n x \cos x-\cos n x \sin x \\
& \Rightarrow \sin x \cos n x=\sin n x \cos x-\sin (n-1) x] \\
& =-\frac{\cos ^m x \cos n x}{n}-\frac{m}{n} \int \cos ^m x \sin n x d x+\frac{m}{n} \int \cos ^{m-1} x \sin (n-1) x d x \\
& I_{m, n}=-\frac{\cos ^m x \cos n x}{n}-\frac{m}{n} I_{m, n}+\frac{m}{n} I_{m-1, n-1}
\end{aligned}
$

$\begin{aligned} & \Rightarrow \frac{m+n}{n} I_{m, n}=-\frac{\cos ^m x \cos n x}{n}+\frac{m}{n} I_{m-1, n-1} \\ & \text { or } \quad I_{m, n}=-\frac{\cos ^m x \cos n x}{m+n}+\frac{m}{m+n} I_{m-1, n-1}\end{aligned}$

NOTE :

In the similar way we can also prove the following result

1. $\int \cos ^m x \cos n x d x=\frac{\cos ^m x \sin n x}{m+n}+\frac{m}{m+n} \int \cos ^{m-1} x \cos (n-1) x d x$
2. $\int \sin ^m x \sin n x d x=\frac{n \sin ^m x \cos n x}{m^2-n^2}-\frac{m \sin ^{m-1} x \cos x \cos n x}{m^2-n^2}+\frac{m(m-1)}{m^2-n^2} \int \sin ^{m-2} x \sin n x d x$
3. $\int \sin ^m x \cos n x d x=\frac{n \sin ^m x \sin n x}{m^2-n^2}-\frac{m \sin ^{m-1} x \cos x \cos n x}{m^2-n^2}+\frac{m(m-1)}{m^2-n^2} \int \sin ^{m-2} x \cos n x d x$

Summary: Reduction formulas help in converting complex problems into simpler ones. It is an important concept in mathematics. It provides a deeper understanding of mathematical ideas paramount for later developments in many scientific and engineering disciplines.

Recommended Video Based on Integration by Reduction Formula

Solved Examples Based on Integration by Reduction Formula

Example 1: Evaluate $\int \sin ^4 x d x$

1) $\frac{1}{8}+\frac{\sin 4 x}{32}+\frac{\sin 2 x}{2}+C$
2) $\frac{\sin (4 x)-8 \sin (2 x)+12 x}{32}+C$
3) $\frac{1}{8}-\frac{\sin 4 x}{32}+\frac{\sin 2 x}{2}+C$

4) none of these

Solution
$
\begin{aligned}
& I=\int \sin ^4 x d x \\
& \Rightarrow I=\int\left(\frac{1-\cos 2 x}{2}\right)^2 d x \\
& =\frac{1}{4} \int\left(1-2 \cos 2 x+\cos ^2 2 x\right) d x \\
& =\frac{1}{4} x-\frac{1}{2} \int \cos 2 x d x+\frac{1}{4} \int \cos ^2 2 x d x \\
& =\frac{1}{4} x-\frac{1}{4} \sin 2 x+\frac{1}{8}\left(x+\frac{1}{4} \sin (4 x)\right) \\
& =\frac{\sin (4 x)-8 \sin (2 x)+12 x}{32}+C
\end{aligned}
$

Hence, the answer is the option (2).

Example 2: Find the value of $\int \sin ^2 x \cos ^2 x d x$

1) $\frac{x}{2}-\frac{\sin 2 x}{2}+C$
2) $\frac{x}{4}-\frac{\sin 4 x}{4}+C$
3) $\frac{1}{8}\left(x-\frac{1}{4} \sin (4 x)\right)+C$
4) $\frac{x}{2}-\frac{\sin 2 x}{4}+C$

Solution

$=\int \sin ^2 x \cos ^2 x d x=\int \frac{\sin ^2(2 x)}{4} d x=\int \frac{1-\cos (4 x)}{8} d x=\frac{1}{8}\left(x-\frac{1}{4} \sin (4 x)\right)+C$

Hence, the answer is the option (3).

Example 3: $\int\left(\tan ^2 x+\cot ^2 x\right) d x$

$\begin{aligned} & \text { 1) } \tan x+\cot x+C \\ & \text { 2) } \tan x+\cot x-2+C \\ & \text { 3) }-2 x+\tan (x)-\cot (x)+C \\ & \text { 4) } \sec x+\csc x+C\end{aligned}$

Solution

$\begin{aligned} & I=\int \tan ^2(x) d x+\int \cot ^2(x) d x \\ & \int \tan ^2(x) d x=\int-1+\sec ^2(x) d x=-x+\tan (x) \\ & \int \cot ^2(x) d x=\int-1+\csc ^2(x) d x=-x-\cot (x) \\ & I=-2 x+\tan (x)-\cot (x)+C\end{aligned}$

Hence, the answer is the option (3).

Example 4: Integrate $\int \tan ^4 x d x$

1) $\frac{\tan ^3 x}{3}-\tan x+C$
2) $\frac{\tan ^3 x}{3}-\tan x+x+C$
3) $\frac{\tan ^3 x}{3}+C$
4) $\frac{\tan ^3 x}{3}+\tan x+C$

Solution

$\begin{aligned} & \int \tan ^4 x d x \\ & =\int \tan ^2 x\left(\sec ^2 x-1\right) d x \\ & =\int \tan ^2 x \sec ^2 x d x-\int \tan ^2 x d x \\ & =\int \tan ^2 x \sec ^2 x d x-\int\left(\sec ^2 x-1\right) d x \\ & =\frac{\tan ^3 x}{3}-\tan x+x+C\end{aligned}$

Hence, the answer is the option (2).

Example 5: Integrate $\int \cot ^5 x d x$

1) $\frac{\cot ^4 x}{4}-\frac{\cot ^2 x}{2}+C$

2) $-\ln (\csc (x))-\frac{\csc ^4(x)}{4}+\csc ^2(x)+c$

3) $\frac{\cot ^4 x}{4}-\cot ^2 x+\ln \sin x+C$

4)None of these

Solution

$\begin{aligned} & \int \cot ^5 x d x=\int \cot x\left(\csc ^2 x-1\right)^2 d x \\ & u=\csc (x): \mathrm{d} x=-\frac{1}{\cot (x) \csc (x)} \mathrm{d} u \\ & =-\int \frac{\left(u^2-1\right)^2}{u} \mathrm{~d} u \\ & =-\ln (\csc (x))-\frac{\csc ^4(x)}{4}+\csc ^2(x)+c\end{aligned}$

Hence, the answer is the option (2).