Rolle’s Theorem: Definition, Formula, Examples, Questions

Rolle's Theorem is an important concept in calculus. It is useful in understanding the relationship between curves and their slopes. The tangent line to the curve is a straight line that touches a curve at a single point without crossing it at that point. These concepts of Tangents and slopes have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Rolle’s Theorem
2. Applications of Rolle’s Theorem
3. Proof of Rolle's Theorem
4. Lagrange’s Mean Value Theorem (LMVT)
5. Recommended Video Based on Rolle's Theorem
6. Solved Examples Based On Rolle's Theorem
7. Summary

In this article, we will cover the concept of Rolle's Theorem. This topic falls under the broader category of Calculus, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of seven questions have been asked on this topic in JEE Main from 2013 to 2023, including two questions in 2020, three questions in 2021, and two in 2022.

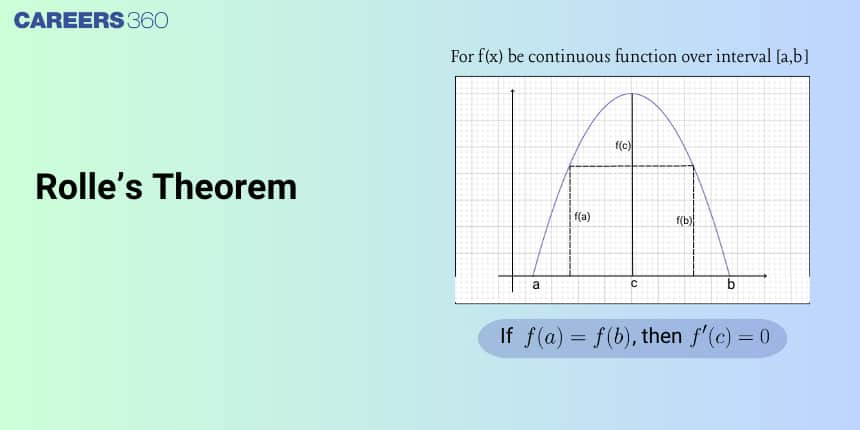
Rolle’s Theorem

Let $f$ be a real-valued function defined on the closed interval $[a, b]$ such that
1. it is continuous on the closed interval $[a, b]$,
2. it is differentiable on the open interval $(a, b)$, and
3. $f(a)=f(b)$.

There then exists at least one $c \in(a, b)$ such that $f^{\prime}(c)=0$.

Geometrical interpretation of Rolle’s Theorem

$f(x)$ be a real-valued function defined on $[a, b]$ such that the curve $y=f(x)$ is continuous in $[\mathrm{a}, \mathrm{b}]$ and it is possible to draw a unique tangent at every point on the curve $y=f(x)$ between points $A$ and $B$. Also, the ordinates at the endpoints of the interval $[a, b]$ are equal. Then there exists at least one point ( $c, f(c)$ ) lying between $A$ and $B$ on the curve $y=f(x)$ where the tangent is parallel to the $x$-axis. I.e. $f^{\prime}(c)=0$.

If the function is continuous and differentiable and if $f(x)=0$ has two roots $\alpha$ and $\beta$, then from Rolle's theorem there exists at least one root of the equation $f^{\prime}(x)=0$ in the interval $(\alpha, \beta)$. Similarly, for twice differentiable function $y=f(x)$, between any two roots of the equation $f^{\prime}(x)=0$, there exists at least one root of the equation $f^{\prime \prime}(x)=0$ and so on.

Note:

• The converse of Rolle’s theorem need not be true.

For example,
$
\begin{aligned}
& \text { Let } f(x)=x^3-x^2-x+1 \text { in the interval }[-1,2] \\
& \mathrm{f}^{\prime}(\mathrm{x})=3 \mathrm{x}^2-2 \mathrm{x}-1 \\
& \mathrm{f}^{\prime}(1)=3(1)^2-2(1)-1=0 \\
& \text { but } \mathrm{f}(-1) \neq \mathrm{f}(2)
\end{aligned}
$

Applications of Rolle’s Theorem

We can use Rolle's theorem to study and calculate the root of the equation as well as locate the roots, The equation must be continuous as well as differentiable.

Let's look at one example
Consider the equation $f(x)=(x-1)(x-2)(x-3)(x-4)$. Then how many roots of the equation $f^{\prime}(x)=0$ are positive?

Let $f(x)=(x-1)(x-2)(x-3)(x-4)$
Since, $f(x)$ is continuous and differentiable and $f(1)=f(2)=f(3)=f(4)=0$

According to Rolle's theorem, there is at least one root of the equation $f^{\prime}(x)=0$ in each of the intervals $(1,2),(2,3)$, and $(3,4)$.

Since $f^{\prime}(x)$ is a cubic function. So $f^{\prime}(x)=0$ has exactly one root in each interval $(1,2),(2$, 3) and (3, 4)

Proof of Rolle's Theorem

consider the portion AB of the curve $y=f(x)$, lying between $x=a$ and $x=b$, such that

(i) It goes continuously from $A$ to $B$

(ii) it has a tangent at every point between $A$ and $B$
(iii) ordinate of $A=$ ordinate of $B$.

From the figure, it is clear that $f(x)$ increases in the interval $A C_1$, which implies that $f^{\prime}(x)>0$ in this region and decreases in the interval $C_1 B$ which implies $f^{\prime}(x)<0$ in this region. Now since there is unique tangent to be drawn on the curve lying in between $A$ and $B$ and since each of them has a unique slope i.e. unique value of $f^{\prime}(x)$

So due to continuity and differentiability of the funtion $f(x)$ in the region A to B , there is a point $\mathrm{x}=\mathrm{c}$, where $f^{\prime}(c)$ should be zero.

Hence $f^{\prime}(c)=0$, where $a<c<b$
Thus, Rolle's theorem was proved.|

Lagrange’s Mean Value Theorem (LMVT)

Lagrange's Mean Value Theorem generalized Rolle's theorem by considering functions that do not necessarily have equal value at the endpoints.

Statement

Let $f(x)$ be a function defined on $[a, b]$ such that
1. it is continuous on $[\mathrm{a}, \mathrm{b}]$,
2. it is differentiable on $(\mathrm{a}, \mathrm{b})$.

Then there exists at least one real number $c \in(a, b)$ such that

$
f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}
$

Geometrical Interpretation:

LMVT states that if $f$ is continuous over the closed interval $[a, b]$ and differentiable over the open interval $(a, b)$, then there exists a point $c \in(a, b)$ such that the tangent line to the graph of $f$ at $c$ is parallel to the secant line connecting $(a, f(a))$ and $(b, f(b))$.

Recommended Video Based on Rolle's Theorem

Solved Examples Based On Rolle's Theorem

Example 1: Let $f$ and $g$ be twice differentiable even functions on $(-2,2)$ such that $\mathrm{f}\left(\frac{1}{4}\right)=0, \mathrm{f}\left(\frac{1}{2}\right)=0, \mathrm{f}(1)=1$ and $\mathrm{g}\left(\frac{3}{4}\right)=0, \mathrm{~g}(1)=2$. Then, the minimum number of solutions of $f(x) g^{\prime \prime}(x)+f^{\prime}(x) g^{\prime}(x)=0$ in $(-2,2)$ is equal to $\qquad$ [JEE Main 2022]
1) $4$
2) $3$
3) $1$
4) $6$

Solution

Let $h(x)=\mathrm{f}(\mathrm{x}) \cdot \mathrm{g}^{\prime}(\mathrm{x})$
So $h(x)$ is continuous and differentiable.
Now as $\mathrm{f}\left(\frac{1}{4}\right)=\mathrm{f}\left(\frac{1}{2}\right)=0$ and $\mathrm{f}(\mathrm{x})$ is even function, so

$\mathrm{f}\left(\frac{-1}{4}\right)=\mathrm{f}\left(\frac{-1}{2}\right)=0$ which means
$\mathrm{h}\left(-\frac{1}{2}\right)=\mathrm{h}\left(-\frac{1}{4}\right)=\mathrm{h}\left(\frac{1}{4}\right)=\mathrm{h}\left(\frac{1}{2}\right)=0$

So $-\frac{1}{2},-\frac{1}{4}, \frac{1}{4}, \frac{1}{2}$ are 4 roots of $\mathrm{h}(\mathrm{x})$
Also $g^{\prime}(0)=0(\mathrm{~g}(\mathrm{x})$ is even diffrential function $\Rightarrow \mathrm{h}(0)=0$
From minimum roots of $\mathrm{h}(\mathrm{x}), \mathrm{g}(\mathrm{x})$ may look something like this

$\therefore \mathrm{h}(\mathrm{x})$ has minimum $5$ roots

$
-\frac{1}{2},-\frac{1}{4}, 0, \frac{1}{4}, \frac{1}{2}
$
So, $h^{\prime}(x)=f^{\prime} g^{\prime}+\mathrm{fg}^{\prime \prime}$ has at least $4$ roots

Hence answer is $4$

Example 2: Let $\mathrm{f}:[0,1] \rightarrow \mathbf{R}$ be a twice differentiable function in $(0,1)$ such that $\mathrm{f}(0)=3$ and $\mathrm{f}(1)=5$. If the line $\mathrm{y}=2 \mathrm{x}+3$ intersects the graph of f at only two distinct points in $(0,1)$, then the least number of points $\mathrm{x} \in(0,1)$, at which $\mathrm{f}^{\prime \prime}(\mathrm{x})=0$, is __________________ . [JEE Main 2022]
1) $2$
2) $1$
3) $7$
4) $4$

Solution

$
\mathrm{f}^{\prime}(\mathrm{a})=\mathrm{f}^{\prime}(\mathrm{b})=\mathrm{f}^{\prime}(\mathrm{c})=2
$
$\Rightarrow \mathrm{f}^{\prime \prime}(\mathrm{x})$ is zero
for at least $\mathrm{x}_1 \in(\mathrm{a}, \mathrm{b}) \& \mathrm{x}_2 \in(\mathrm{b}, \mathrm{c})$

Hence, two number of points.

Example 3: If $c$ is a point at which Rolle's theorem holds for the function, $f(x)=\log _e\left(\frac{x^2+\alpha}{7 x}\right)$ in the interval $[3,4]$, where $\alpha \in R$ then $f^{\prime \prime}(c)$ is equal to :
[JEE Main 2020]
1) $-\frac{1}{24}$
2) $-\frac{1}{12}$
3) $\frac{\sqrt{3}}{7}$
4) $\frac{1}{12}$

Solution

$\begin{aligned} & f(3)=f(4) \\ & \frac{9+\alpha}{3}=\frac{16+\alpha}{4} \\ & \alpha=12 \\ & f^{\prime}(x)=\frac{x^2-12}{x\left(x^2+12\right)} \\ & f^{\prime}(c)=0 \\ & \therefore \quad c=\sqrt{12} \\ & \therefore \quad f^{\prime \prime}(c)=\frac{1}{12}\end{aligned}$

Hence, the answer is the option (4).

Example 4: Let $f:(a, b) \rightarrow \mathbf{R}$ be twice differentiable function such that $f(\mathrm{x})=\int_a^{\mathrm{x}} \mathrm{g}(\mathrm{t}) \mathrm{dt}$ for a differentiable function $g(x)$. If $f(x)=0$ has exactly five distinct roots in (a, b), then $g(x) g^{\prime}(x)=0$ has at least: [JEE Main 2021]
1) Twelve roots in $(a, b)$
2) Five roots in $(a, b)$
3) Seven roots in $(a, b)$
4) Three roots in $(a, b)$

Solution

$
f(x)=\int_a^x g(t) d t
$
Differentiating
$
\begin{aligned}
& f^{\prime}(x)=g(x) \cdot 1-g(a) \cdot 0 \\
& f^{\prime}(x)=g(x) \\
& \Rightarrow f^{\prime \prime}(x)=g^{\prime}(x)
\end{aligned}
$

Now $f(x)$ has $5$ roots in $(a, b)$

$\Rightarrow f^{\prime}(x)(=g(x))$ has at least 4 roots in $(a, b)$. $\& g^{\prime}(x)$ has at least 3 roats in $(a, b)$
So $g(x) \cdot g^{\prime}(x)$ has at least $7$ roots in $(a, b)$.

Hence, the answer is the option (3).

Example 5: Let $f$ be any continuous function on $[0,2]$ and twice differentiable on $(0,2)$. If $f(0)=0, f(1)=1$ and $f(2)=2$, then: [JEE Main 2021]
1) $f^{\prime \prime}(x)>0$ for all $x \in(0,2)$
2) $f^{\prime}(x)=0$ for some $x \in[0,2]$
3) $f^{\prime \prime}(x)=0$ for some $x \in(0,2)$
4) $f^{\prime \prime}(x)=0$ for all $x \in(0,2)$

Solution

Let $g(x)=f(x)-x$

$
\begin{aligned}
& g(0)=0 \\
& g(1)=0 \\
& g(2)=0
\end{aligned}
$
Apply Rolle's Therom for $g(x)_{\text {in }}[0,1]$
There exist a $C_1 \in(0,1)$ s.t.

$
\begin{aligned}
& g^{\prime}\left(C_1\right)=0 \\
& \Rightarrow f^{\prime}\left(C_1\right)-1=0 \\
& \Rightarrow f^{\prime}\left(C_1\right)=1
\end{aligned}
$

Rolle's theorem in $[1,2]$ for $g(x)$
There exist a $C_2 \in(1,2)$ s.t

$
g^{\prime}\left(C_2\right)=0 \Rightarrow f^{\prime}\left(C_2\right)-1=0 \Rightarrow f^{\prime}\left(C_2\right)=1
$

Rollo's theorem in $\left[C_1, C_2\right]$ for $f^{\prime}(x)$
$\Rightarrow$ There exist a $C \in\left(C_1, C_2\right) \in(0,2)$, s.t

$
f^{\prime \prime}(C)=0
$

Hence, the answer is the option (3).

Summary

Rolle's theorem is an important concept of mathematics. Lagrange's Mean Value Theorem(LMVT) is a special case of Rolle's theorem. Rolle's theorem states that there exists at least one root of the equation $f^{\prime}(x)=0$ in the interval $(\alpha, \beta)$. This concept is applied in various fields of mathematics.