Sign of Quadratic Expression: Formulas, Methods, and Examples

The sign of a quadratic expression is essential for solving inequalities and analyzing the behavior of the quadratic functions. A quadratic expression is $a x^2+b x+c$ where a , b , and c are constants, and $a \neq 0$. The sign of this expression depends on the values of $a, b$, and $c$, as well as the roots (if they exist) of the quadratic equation.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

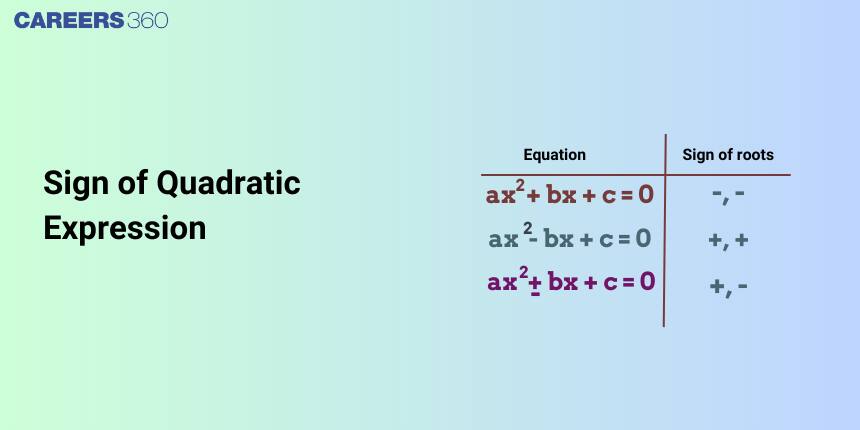
In this article, we will cover the concept of the sign of quadratic expression. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

Steps to determine the sign of quadratic equation

Let $y=a x^2+b x+c=0$ be the quadratic equation, such that $a$ is non-zero and $a, b, c$ are real numbers, then
1. If $D<0$ then we know quadratic equation has no real roots. So for all real value of x , the graph never intersects or touches $x$ axis, so it is always above or below $x$ axis. This means that the value of $y$ will always be positive or negative,

If $a>0$ and $\mathrm{D}<0$ :
The graph open upwards hence all values of $y$ will be positive as graph can't start from below $x$-axis (because if it happens then it will cut $x$ - axis as it is opening upwards, but it has no solution) so it starts from above $x$-axis and hence $y$ is +ve for all values of $x$.

In similar way if $\mathrm{a}<\mathbf{0}$ and $\mathrm{D}<\mathbf{0}$ then y is -ve for all values of $x$ -axis.

2. If $D=0$, then the quadratic equation $y$ will have one real solution, so $y=0$ for one particular value of $x$ and for all rest value of $x$, $y$ will be $+ve$ or $-ve$ depending upon value of $a$. If $a>0$, then the graph will open upwards so $y$ will be $+ ve$ otherwise if $a < 0$, then $y$ will be $-ve$.

3. If D > 0, then the quadratic equation y will have two real solution $x_1$ and $x_2$, so if a > 0 then y = 0 on $x_1$ and $x_2$, and between the solution ($x_1$ < x < $x_2$), y will be -ve and left (for x < $x_2$ ) and right (x > $x_1$) part of the solution will give +ve value of y

If a < 0, exactly the opposite will happen, y = 0 on $x_1$ and $x_2$, and between the solution ($x_1$ < x < $x_2$), y will be $+ve$ and left (for $x < x_2$ ) and right ($x > x_1$) part of the solution will give $-ve$ value of $y$.

Note

If $f(x)=a x^2+b x+c$, then linear expressions can be identified in terms of functions at some constant value

Eg,
- $a+b+c=a .1^2+b .1+c=f(1)$
- $9 a+3 b+c=a .3^2+b .3+c=f(3)$
- $4 a-2 b+c=a \cdot(-2)^2+b \cdot(-2)+c=f(-2)$
- $c=a .0^2+b .0+c=f(0)$
- $8 \mathrm{a}-4 \mathrm{~b}+2 \mathrm{c}=2(4 \mathrm{a}-2 \mathrm{~b}+\mathrm{c})=2 . \mathrm{f}(-2)$

Summary

The sign of a quadratic equation is crucial for solving quadratic inequalities by analyzing the behaviour of quadratic functions in various mathematical and applied contexts. By mastering the determination of the sign of quadratic expressions, one gains a powerful tool for analyzing and solving a wide range of mathematical problems and enhancing their overall understanding of algebra and its applications. This also helps in further solving inequalities at the higher stage of mathematical learning. It forms the base for algebraic branch of mathematics.

Recommend Video:

Solved Examples Based on Sign of Quadratic Equations

Example 1: If $x^2+2(a-1) x+(a+5)>0 \forall x \in R$ then:
1) $[-1,4]$
2) $(-1,4)$
3) $(-1,4]$
4) $[-1,4)$

Solution:
As we learned in
Sign of quadratic expression as positive. -
$a x^2+b x+c$ will be always positive for all $x \epsilon R$, if $a>0 \& b^2-4 a c<0$
(Where $a, b, c \in R)$
- wherein

So, the graph $y=a x^2+b x+c$ will be always above the $x$ -axis so $a x^2+b x+c=0$ has no real roots.

quadratic is always positive when

$
a>0 \space, D<0
$

here coeff of $x^2>0$ so only $D<0$ is required.

$
\begin{aligned}
& \Rightarrow 4(a-1)^2-4(a+5)<0 \\
& \Rightarrow a^2-3 a-4<0 \\
& \Rightarrow(a-4)(a+4)<0 \\
& \Rightarrow a \in(-1,4)
\end{aligned}
$
Hence, the answer is the option (2).

Example 2: Number of integer values of ' $a^{\prime}$ for which $x^2+2(a-1) x+a \geqslant-5 \forall x \in R$ is:

Solution:
As we learned in
Quadratic Expression $a x^2+b x+c$ is non negative -
$a x^2+b x+c \geqslant 0$ for all $x \in R$ When $a>0 \& b^2-4 a c \leq 0$

$
x^2+2(a-1) x+(a+5) \geqslant 0 \forall n \in R
$
So $D \leqslant 0$ is the only required condition here as the coefficient of $x^2$ is already positive.

$
\begin{aligned}
& 4(a-1)^2-4(a+5) \leqslant 0 \Rightarrow(a-4)(a+1) \leqslant 0 \\
& \Rightarrow a \in[-1,4]
\end{aligned}
$
Hence, the answer is (6).

Example 3: The number of integral values of $m$ for which the quadratic expression, $(1+2 m) x^2-2(1+3 m) x+4(1+m), x \in R$, is always positive, is :
Solution:
Quadratic Expression $\mathrm{ax}^2+\mathrm{bx}+\mathrm{c}$ is always positive $\left(a x^2+b x+c>0\right.$ for all $\left.x \epsilon R\right)$ when

$
a>0 \& \mathrm{D}<0(a, b, c \in R)
$

Now,

$
\begin{aligned}
& a>0 \\
& \Rightarrow 1+2 m>0 \\
& \Rightarrow m>-1 / 2 \\
& \text { and } \mathrm{D}>0 \\
& 4(1+3 m)^2-4(1+2 m) \times 4(1+m)<0 \\
& m^2-6 m-3<0 \\
& \Rightarrow m=3 \pm \sqrt{12} \\
& \Rightarrow m \epsilon(3-2 \sqrt{3}, 3+2 \sqrt{3}) \text { and } m>-1 / 2
\end{aligned}
$
The integral value of $m$

$
=0,1,2,3,4,5,6
$

Hence, the answer is $7$.

Example 3: The values of ' $a$ ' for which $-x^2+x-a<0 \forall x \in R$ is
1) $
a>-2
$

2) $
a>-1
$

3) $
a>\frac{1}{4}
$

4) $
a>0
$

Solution:

As we learned in

Value of quadratic expression as negative
$a x^2+b x+c$ will be always negative, for all $x \in R$, If $a<0 \& b^2-4 a c<0$ (Where $\left.a, b, c \in R\right)$
Now

Coeff of $x^2=-1<0$

$
D<0 \Rightarrow 1-4 a<0 \Rightarrow a>\frac{1}{4}
$
Hence, the answer is the option (3).

Example 4: Values of ' $a$ ' for which $x^2-a x+a \geqslant 0 \forall x \in R$ are:
1) $
a \in R
$

2) $
a \in(0,5)
$

3) $
a \in R^{+}
$

4) $
a \in[0,4]
$

Solution:

As we learned in
Quadratic Expression $a x^{\wedge} 2+b x+c$ is non negative -
$a x^2+b x+c \geqslant 0$ for all $x \in R$ When $a>0 \& b^2-4 a c \leq 0 \quad(a, b, c \in R)$ coeff of $x^2=1>0$, so only other required condition is $D \leqslant 0$

$
\begin{aligned}
& \Rightarrow a^2-4 a \leqslant 0 \\
& \Rightarrow a \epsilon[0,4]
\end{aligned}
$
Hence, the answer is the option (4).

Example 5: The number of integral values of $m$ for which the quadratic expression, $(1+2 m) x^2-2(1+3 m) x+4(1+m), x \in R$ is always positive, is :
1) $6$
2) $7$
3) $8$
4) $3$

Solution:

Quadratic Expression $\mathrm{ax}^2+\mathrm{bx}+\mathrm{c}$ is always positive $\left(a x^2+b x+c>0\right.$ for all $\left.x \in R\right)$ when $a>0 \& \mathrm{D}<0(a, b, c \in R)$

Now,

$
\begin{aligned}
& a>0 \\
& \Rightarrow 1+2 m>0 \\
& \Rightarrow m>-1 / 2
\end{aligned}
$

and $D>0$

$
\begin{aligned}
& 4(1+3 m)^2-4(1+2 m) \times 4(1+m)<0 \\
& m^2-6 m-3<0 \\
& \Rightarrow m=3 \pm \sqrt{12} \\
& \Rightarrow m \epsilon(3-2 \sqrt{3}, 3+2 \sqrt{3}) \text { and } m>-1 / 2
\end{aligned}
$
The integral value of $m$

$
=0,1,2,3,4,5,6
$

Hence, the answer is the option 2.