Square root of complex numbers

The square root of complex numbers is similar to the square root of real numbers but the procedure to find square root is different from real numbers. Just like real numbers, finding the square root of a complex number involves identifying a number that, when squared, returns the original complex number. This requires understanding both the algebraic and geometric representations of complex numbers.

This Story also Contains

1. Complex Number
2. What is the Square Root of a Complex Number?
3. Square Root of Complex Number in Polar Form
4. Solved Examples Based on Square Root of Complex Numbers

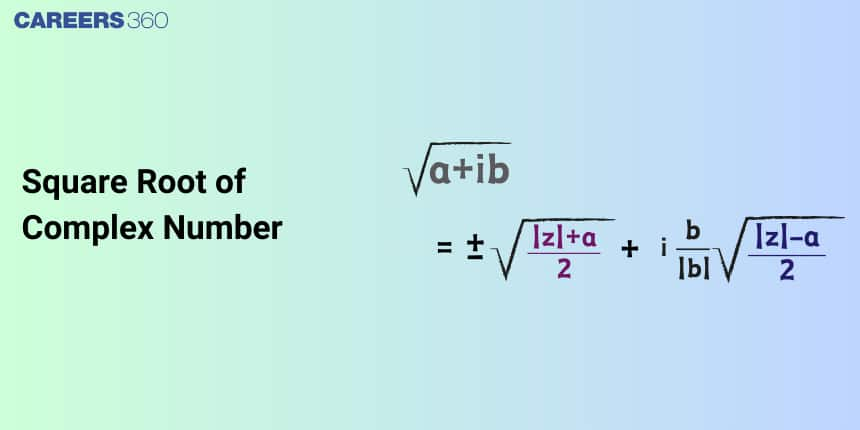
In this article, we will cover the concept of the square root of complex numbers. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of three questions have been asked on this concept, including two in 2017, and one in 2020.

Complex Number

The number which has no real meaning then these numbers are represented in complex forms. The general form of complex numbers are $a+i b$ where i is iota or$\sqrt{-1}$.

A number of the form $a+i b$ is called a complex number (where a and b are real numbers and i is iota). We usually denote a complex number by the letter $z, z_1, z_2$, etc

For example, $z=5+2 i$ is a complex number.

5 here is called the real part and is denoted by $\operatorname{Re}(z)$ , and 2 is called the imaginary part and is denoted by $\operatorname{Im}(z)$

What is the Square Root of a Complex Number?

A complex number's square root is equal to another complex number whose square equals the original complex number. For example, if $\sqrt{ }(a+i b)=x+i y$ is the square root of the complex number $a+i b$, then $(x+i y) 2=a+i b$. Finding the values of x and y by squaring both sides of the equation $\sqrt{ }(a+i b)=x+i y$ and comparing the real and imaginary parts is one easy method to obtain the square root of a complex integer, a + ib. Let's look at the formula for calculating a complex number's square root.

How to find the square root of complex numbers?

Let $z=x+i y$, is the complex number whose square root we have to find

Since the square root of a complex number must be a complex number,

so let $z^{1 / 2}=a+i b$

Now squaring both sides

$z=x+i y=(a+i b)^2=a^2-b^2+2 i a b$

Now compare real and imaginary parts and find the value of $a$ and $b$ in terms of $x$ and $y$
$
\begin{aligned}
& a^2-b^2=x \\
& 2 a b=y \\
& a^2+b^2=\sqrt{\left(a^2-b^2\right)^2+4 a^2 b^2}=\sqrt{x^2+y^2}=|z|
\end{aligned}
$
By solving (i) and (iii) we get

$
2 a^2=x+|z| \Rightarrow a= \pm \sqrt{\frac{x+|z|}{2}}
$
Similarly we find $b= \pm \sqrt{\frac{|z|-x}{2}}$
So $\sqrt{\mathrm{z}}= \pm\left(\sqrt{\frac{|z|+\operatorname{Re}(\mathrm{z})}{2}}+\mathrm{i} \sqrt{\frac{|\mathrm{z}|-\operatorname{Re}(\mathrm{z})}{2}}\right)$

if Im(z) > 0 otherwise there will be a -ve sign between the real and imaginary parts of the square root of z.

Square Root of Complex Number in Polar Form

The $n^{th}$ root theorem for complex numbers is used to find the square root of a complex number in polar form. According to the nth Root Theorem, if a complex number $z=r(\cos \theta+i \sin \theta)$ is known, then $z_1 / n=$ $\mathrm{r_1}/ \mathrm{n}[\cos [(\theta+2 \mathrm{k} \pi) / \mathrm{n}]+\mathrm{i} \sin [(\theta+2 \mathrm{k} \pi) / n]]$, where $\mathrm{k}=0,1,2,3, \ldots, n-1$, represents the nth root. We add $2 \mathrm{k} \pi$ to $\theta$ to get the complex number's periodic roots. Therefore, we can get the formula to find the square root of a complex number in polar form using the nth root formula. The equation is $Z_1 / 2$ is equal to $r_1 / 2[i \sin [(\theta+2 k \pi) / 2]+\cos [(\theta+2 k \pi) / 2]$ in which $k=0,1$

Note:

1. Students do not need to remember this formula. However, they are required to know the procedure to find the square root of a complex number.

2. If $a+i b$ is one of the square roots of $z$, then the other square root must be $-(a+i b)$

Recommended Video Based on Square Root of Complex Numbers:

Solved Examples Based on Square Root of Complex Numbers

Example 1: If $(x+i y)^2=7+24 i$ then a value of $(7+\sqrt{-576})^{1 / 2}-(7-\sqrt{-576})^{1 / 2}$ is:

Solution:

As we learned in

Square Root of a Complex Number -
$
\sqrt{z}=a+i b \text { where } z=x+i y
$

is calculated by equating real and imaginary parts of $x+i y=(a+i b)^2$

We have to find $(7+24 i)^{1 / 2}-(7-24 i)^{1 / 2}$

Now $(x+i y)^2=7+24 i$

$x+i y=\sqrt{7+24 i}$

and $x-i y=\sqrt{7-24 i}$ (Put - i at the place of i)

$\therefore \quad i 2 y=\sqrt{7+24 i}-\sqrt{7-24 i}$

Now $x^2-y^2+i 2 x y=7+24$

$\therefore \quad x^2-y^2=7, x y=12$

Solving we get $x= \pm 4 ; y \pm 3$,

$\therefore \quad i 2 y= \pm 6 i$

$\therefore-61$

Hence, the answer is -6i.

Example 2: The region represented by $\{z=x+i y \in C:|z|-\operatorname{Re}(z) \leq 1\}$ is also given by

1) $y^2 \geq 2(x+1)$

2) $y^2 \leq 2(x+1 / 2)$

3) $y^2 \leq(x+1 / 2)$

4) $y^2 \geq\left(x^2+1\right)$

Solution

$\begin{aligned} & |z|-\operatorname{Re}(z) \leq 1 \\ & \Rightarrow \sqrt{x^2+y^2}-x \leq 1 \\ & \Rightarrow \sqrt{x^2+y^2} \leq 1+x\end{aligned}$

$\begin{aligned} & \Rightarrow x^2+y^2 \leq 1+x^2+2 x \\ & \Rightarrow y^2 \leq 2(x+1 / 2)\end{aligned}$

Hence, the answer is the option 2.

Example 3: One of the square roots of $21-20 i$ equals.

Solution:

Let a + ib be the square root

So, $(a+i b)^2=21-20 i$

$a^2-b^2+i(2 a b)=21-20 i$

Thus,

$\begin{aligned} & a^2-b^2=21 \text { and } 2 a b=-20 \\ & a^2-b^2=21 \text { and } a h=-10\end{aligned}$

Using the relation $\left(a^2+b^2\right)^2=\left(a^2-b^2\right)^2+4 a^2 b^2$
$
\begin{aligned}
& \left(a^2+b^2\right)^2=21^2+20^2=841 \\
& a^2+b^2=29
\end{aligned}
$

Adding this equation to $\mathrm{a}^2-\mathrm{b}^2=21$, we get

$a^2=25$

$\therefore a=5$ or $a=-5$

Now using ab = -10, when a= 5 then b= -2 and when a =-5, b= 2

$a+i b=5-2 i$ or $-5+2 i$

Hence, the answer is -5+2i.

Example 4: If $(x+i y)^2=7+24 i$then the value of $(7+\sqrt{-576})^{\frac{1}{2}}-(7-\sqrt{-576})^{\frac{1}{2}}$ is

Solution:
$
\begin{aligned}
& (x+i y)^2=x^2-y^2+2 x y i \\
\Rightarrow & 7+24 i=x^2-y^2+2 x y i \\
\Rightarrow & x^2-y^2=7 \text { and } 2 i x y=24 i \\
\Rightarrow & x^2-y^2=7 \text { and } x y=12
\end{aligned}
$

now start taking values of $x$ and $y$

$
\begin{aligned}
& x= \pm 4 \text { and } y= \pm 3 \\
& (x+i y)-(x-i y)=2 i y= \pm 6 i
\end{aligned}
$
Hence, the answer is -6i.

Example 5: If $z=x-i y$ and $z^{\frac{1}{3}}=p+i q$ then $\frac{\left(\frac{x}{p}+\frac{q}{q}\right)}{\left(p^2+q^2\right)}$ is equal to

Solution:

Equality in Complex Numbers -

$z=x+i y \& w=a+i b$ are equal if $x=a \& y=b$

where in

Two complex numbers are equal if real parts as well as imaginary parts are equal.

$p=x-i y \quad$ and $z^{1 / 3}=p+i d$

$\begin{aligned} & \therefore \quad z=(p+i q)^3 \\ & \therefore x-i y=p^3+(i q)^3+3 p \cdot i q(p+i q)=p^3+i^3 q^3+i p^2 q-3 p q^2 \\ & x-i y=\left(p^3-3 p q^2\right)+i\left(3 p^2 q-q^3\right)\end{aligned}$

Compare: $p^3-3 p q^2=x$

$p\left(p^2-3 q^2\right)=x$

$p^2-3 q^2=\frac{x}{p}$

and $q\left(3 p^2-q^2\right)=-y$

$q^2-3 p^2=\frac{y}{q}$

$\therefore \frac{\frac{x}{p}+\frac{y}{q}}{p^2+q^2}=\frac{p^2-3 q^2+q^2-3 p^2}{\left(p^2+q^2\right)}=\frac{-2\left(p^2+q^2\right)}{p^2+q^2}=-2$

Hence, the answer is -1.