Straight Lines - Definition, Equations, Properties and Examples

Straight Lines in Mathematics

A straight line is an infinite length extending in both directions. Every equation of the first degree in $x, \text{and} \space y$ represents a straight line. The general equation of a straight line is given as $ax+b y+c=0$ where $a, b,$ and $c$ are real numbers, and at least one of $a$ and $b$ is non-zero.

Types of Straight Lines

The types of straight lines based on their position and relation with other lines are mentioned below:

Properties of Straight Lines

The properties of straight lines include,

• The length of the straight line is infinite

• A straight line gives the shortest distance between two points

• Straight lines do not have any curves or bends.

• Straight lines are one-dimensional

• A straight line does not have area or volume

Slope of a Straight Line

In mathematics, the change of the $y$-axis coordinate with respect to the change of the $x$-axis coordinate is called the Slope of a line. It is the ratio of vertical change to horizontal change between two points on a line. It measures the steepness and direction of the line. The slope of a straight line is denoted by $m$.

• The slope of a line with given two points $(x_1,y_1)$ and $(x_2,y_2)$ is $m = \frac{y_2-y_1}{x_2-x_1}$

• The slope of a line with a given angle $\theta$ is $ m = \tan \theta $

• The slope of a line from the equation of the line of the form $y=mx+c$ is the coefficient of the variable $x$, which is $m$.

Types of Slopes

Slope of a straight line can be of different types.

• Uphill slopes

• Downhill slopes

• Horizontal slopes

• Vertical slopes

Uphill Slopes

The slope of a straight line extending upwards from left to right is called the uphill slope. It is also called a positive slope, as the calculated slope will yield a positive value. In this type of slope, when the value of $x$ increases, the value of $y$ also increases.

Downhill Slope

The slope of the straight line extending downwards from left to right is called the downhill slope. It is also called a negative slope, as the calculated slope will yield a negative value. In this type of slope, when the value of $x$ increases, the value of $y$ decreases.

Horizontal Slope

The slope of a horizontal line is called the horizontal slope. This is also called a zero slope, as the calculated slope will yield the value $0$. In this type of slope, when the value of $x$ increases, the value of $y$ remains the same. That is, the line remains flat.

Vertical Slope

The slope of a vertical line is called the vertical slope. This is also called an infinite slope, as the slope is undefined. In this type of slope, when the value of $y$ increases, the value of $x$ remains the same. That is, the line will be straight up or down.

Notes:

• The slope of a horizontal line is $0$

• The slope of a vertical line is undefined

• The slope of parallel lines $l_1$ and $l_2$ with slopes $m_1$ and $m_2$ is equal (i.e) $m_1 = m_2$

• The product of the slopes of two perpendicular lines $l_1$ and $l_2$ with slopes $m_1$ and $m_2$ is $1$ (i.e) $m_1.m_2 = 1$

Equation of a straight line

The equation of a straight line in various forms is point-slope form, slope-intercept form, standard form, etc. These forms help us understand how to find the equation of a straight line with the given information. Let’s discuss each form in detail.

Equation of Horizontal and Vertical lines

• Horizontal Line: A horizontal line has a slope of zero. Its equation is of the form $y = c$, where $c$ is the $y$-coordinate of any point on the line.

• Vertical Line: A vertical line has an undefined slope. Its equation is of the form $x = a$, where $a$ is the $x$-coordinate of any point on the line.

Example: $y=2$ is a horizontal line and $x=4$ is a vertical line.

Point-slope form of a Straight line

The point-slope form is used to determine the equation of a straight line passing through a point $(x_1,y_1)$ and having slope $m$. The point-slope form of a straight line is given by $y-y_1=m(x-x_1)$

Example: The straight line equations with $m = 2$ and passing through $(3,4)$ is

$(y-4)=2(x-3)$ ⇒ $2x-y=2$

Two points form of a line

The straight line equations passing through $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$\frac{x-x_1}{x_1-x_2}=\frac{y-y_1}{y_1-y_2}$

Example: The equation of a line passing through $(1,2)$ and $(3,5)$ is

$\frac{x-1}{1-2}=\frac{y-3}{3-5}$

⇒ $2x-2=y-3$

⇒ $2x-y+1=0$

Slope-intercept form of a line

If a line is given with its slope m and its $y$-intercept. Say, a line intersects the $y$-axis at the point $(0, c)$. Using the point-slope form of a straight line, we have $y - c = m (x - 0) ⇒ y = mx + c$, where $c$ is the $ y$-intercept. This is called the slope-intercept form of a line.

Example: The equation of a line with slope $m=3$ and $y$-intercept $4$ is $y=3x+4$.

Intercept form of a line

The intercept form is used when the intercepts on the $x$-axis and $y$-axis are known. It is given by: $\frac{x}{a}+\frac{y}{b}=1$, where $a$ is the $x$-intercept and $b$ is the $y$-intercept.

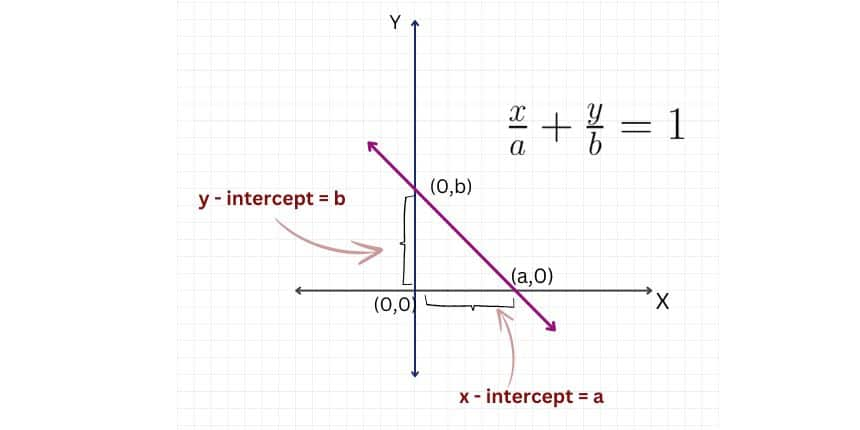
Example: For $x$-intercept as $4$ and $y$-intercept as $5$, the equation of line becomes $\frac{x}{4}+\frac{y}{5}=1$

The normal form of a line

The normal form of a line’s equation involves the perpendicular (normal) distance from the origin to the line. It is given by: $x\cos\alpha + y\sin\alpha=p$

Where $p$ is the length of the perpendicular from the origin to the line, and $\alpha$ is the angle between this perpendicular and the positive $x$-axis.

Example: For $p=5$ and $\alpha=30°$, the equation of the line becomes

$x\cos 30° + y\sin 30° = 5$ ⇒ $\sqrt{3}x+y=10$

Standard form of a line

The standard form of a straight line is given by $ax + by + c = 0$, where $a, b, c$ are real numbers.

Example: The equation of a line in standard form is $2x + 3y + 5 = 0$.

Angle Between Two Straight Lines

The angle($θ$) between two lines with slopes $m_1$ and $m_2$ can be found by using the formula:

$\tan θ = \frac{m_1-m_2}{1+m_1m_2}$

If the value of $\frac{m_1-m_2}{1+m_1m_2}$ is positive, then the angle between the lines is acute.

If the value of $\frac{m_1-m_2}{1+m_1m_2}$ is negative, then the angle between the lines is obtuse.

Distance between Two Points on a Line

The distance between two points on a line $(x_1,y_1)$ and $(x_2,y_2)$ is $d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$

Important Formulae for Straight Lines

This section provides all the important formulae for straight lines in one place, including slope, distance, angle, and various forms of line equations.

Straight Lines in Mathematics: Solved Previous Year Questions

Question 1:

If $a+2 b+c=0$, then the line $a x+b y+c=0$ always passes through which of the following points:

Answer:

$
\begin{aligned}
& a+2 b+c=0 \Rightarrow c=-a-2 b \\
& \therefore a x+b y+c=0 \\
& \Rightarrow a x+b y-a-2 b=0 \\
& \Rightarrow a(x-1)+b(y-2)=0---(i)
\end{aligned}
$
Comparing it to $\mu L_1+\lambda L_2=0$, this equation represents a family of lines passing through the point of intersection of $x-1=0$ and $y-2=0$, which is $(1,2)$
$\therefore$ All lines of type $a x+b y+c=0$ will pass through $(1,2)$ if $a+2 b+c=0$

Hence, the correct answer is $\left ( 1,2 \right )$.

Question 2:

The equation of the line passing through the point of intersection of lines $\mathrm{y}=\mathrm{x}$ and $x+y+3=0$ and which is parallel to line $2 x+3 y=0$ is:

Answer:

Let the required line be

$
\begin{aligned}
& (x+y+3)+\lambda(y-x)=0 \\
& \Rightarrow(1-\lambda) x+(1+\lambda) y+3=0
\end{aligned}
$
Given that it is parallel to $2 x+3 y=0$

$
\begin{aligned}
& \therefore \text { its slope }=\frac{-2}{3} \\
& \Rightarrow \frac{-(1-\lambda)}{1+\lambda}=\frac{-2}{3} \\
& \Rightarrow 3(1-\lambda)=2(1+\lambda) \\
& \Rightarrow 3-3 \lambda=2+2 \lambda \\
& \Rightarrow 5 \lambda=1 \\
& \Rightarrow \lambda=\frac{1}{5}
\end{aligned}
$

$\therefore$ Line is

$
\begin{aligned}
& \left(1-\frac{1}{5}\right) x+\left(1+\frac{1}{5}\right) y+3=0 \\
& \Rightarrow 4 x+6 y+15=0
\end{aligned}
$

Hence, the correct answer is 4x+6y+15= 0.

Question 3:

The lines $x+2 y-3=0,2 x+y-3=0$, and the line are concurrent. If the line passes through the origin, then its equation is:

Answer:

Intersection point of $x+2 y-3=0$ and $2 x+y-3=0$ is $(1,1)$
$\therefore$ line passes through $(1,1)$ and $(0,0)$
$\therefore$ the equation of a line is

$
\begin{aligned}
& y-0=\frac{1-0}{1-0}(x-0) \\
& \Rightarrow y=x \\
& \Rightarrow x-y=0
\end{aligned}
$

Hence, the correct answer is $x-y=0$.

Question 4:

Equation of the line which is perpendicular to $3 x-4 y+2=0$ and passes through $(2,0)$ is:

Answer:

As the line is perpendicular to $3 x-4 y+2=0$, so let $4 x+3 y+c=0$ be the required line.

Now (2.0) lies on this line, so it should satisfy its equation

$
4(2)+3(0)+c=0 \Rightarrow c=-8
$

$\therefore$ Line is $4 x+3 y-8=0$

Hence, the correct answer is $4 x+3 y-8=0$.

Question 5:

The equation of the bisector of the acute angle between the lines $3 x-4 y+7=0$ and $12 x+5 y-2=0$ is:

Answer:

$
\begin{aligned}
& L_1: 3 x-4 y+7=0 \Rightarrow a_1=3, b_1=-4 \\
& L_2: 12 x+5 y-2=0 \Rightarrow a_2=12, b_2=5
\end{aligned}
$
$
\therefore a_1 a_2+b_1 b_2=36-20=16>0
$

$\therefore$ Acute bisector will be given by the negative sign

$
\begin{aligned}
& \text { Equation } \\
& \frac{3 x-4 y+7}{\sqrt{3^2+4^2}}=\frac{-(12 x+5 y-2)}{\sqrt{12^2+5^2}} \\
& \Rightarrow 13(3 x-4 y+7)=5(-12 x-5 y+2) \\
& \Rightarrow 39 x-52 y+91=-60 x-25 y+10 \\
& \Rightarrow 99 x-27 y+81=0 \\
& \Rightarrow 11 x-3 y+9=0
\end{aligned}
$

Hence, the correct answer is $11x-3y+9= 0$.

List of Topics related to straight lines according to NCERT/JEE Mains

This section outlines the key topics under straight lines, as per the NCERT and JEE Main syllabus. These topics will help you gain better conceptual clarity.

Straight Lines in Different Exams

The chapter Straight Lines is a fundamental part of coordinate geometry that deals with representing and analysing lines on a plane using algebraic equations. It is an important topic in Class 11 Mathematics and is frequently tested in board as well as competitive examinations. Questions from this chapter assess a student’s understanding of slopes, different forms of equations of a line, and the geometric interpretation of results. Regular practice of NCERT problems and a clear understanding of formulas help students master this chapter and score well in exams.

Important Books and Resources for Straight Lines

Here you will find recommended books and resources that explain straight-line concepts, equations, and problem-solving techniques with clarity.

NCERT Resources for Straight Lines

This section highlights the NCERT textbook chapters that introduce straight lines and build conceptual understanding for Class 11 and competitive exams.

• NCERT Maths Notes for Class 11th Chapter 10 Straight Lines

• NCERT Maths Solutions for Class 11th Chapter 10 Straight Lines

• NCERT Maths Exemplar Solutions for Class 11th Chapter 10 Straight Lines

NCERT Subjectwise Resources

This section provides NCERT exemplar solutions, detailed notes, and step-by-step solutions to strengthen your preparation.

Practice Questions based on Straight Lines

Here you will get a collection of practice problems to apply straight line formulas, improve accuracy, and boost exam readiness.

Conclusion

The chapter Straight Lines lays a strong foundation for coordinate geometry by helping students understand linear relationships and their graphical representation. By mastering concepts such as slope, equations of a line in different forms, and conditions for parallel and perpendicular lines, students develop clarity and confidence in solving geometric problems. This chapter is essential for Class 11 Mathematics and plays a crucial role in higher-level topics and competitive exams like JEE. With regular practice of NCERT problems and a clear understanding of formulas, students can easily score well and apply these concepts to real-life situations.