“mg” Unit Full Form
Introduction

The term “mg” is an abbreviation for milligrams.
At first impression, it appears that the “mg” is an abbreviation. Yes, you are, absolutely, correct. But it also represents a unit. Before you gather from here, the full form of the “mg” unit and its functionalities, first you have to acquaint yourself with the “units of measurement” that often accompany a number.
On adding some unit of measurement (like a gram, a meter, etc.) to any number say “80000”, its implication gets changed. It then refers to some physical quantity (like “80,000 meters” long route or“80,000 grams” of flour). Isn’t it right? Let us dive into it to explore further.
What Is A Unit Of Measurement?
Look, in day-to-day life, you come across innumerable physical quantities, and for a valid reason, you need to measure them. You may be curious about “How much time is spent doing your homework?”, “What is the mass of sugar in a jar?”, “How long are you now?”, etc.
All these physical quantities like “length“, “time”, etc. have some predefined units of measurement, like “meter”, “second”, etc.
The unit of measurement of a physical quantity is the definite amount of that physical quantity which is well-defined and universally accepted for measuring the same kind of physical quantity worldwide.
The “gram” is, basically, the unit of measurement of mass in the“MKS(Meter Kilogram Second) system”.
Several prefixes are introduced and universally accepted to denote the subdivisions and the multiples of any “unit of measurement”. You can denote the specific subdivisions and multiples of any “unit” by aptly using these predefined prefixes with the “unit of measurement”.
Here, note the following prefixes with their inherent meanings.
The prefix “Milli” denotes “one-thousand parts”.
\[''milli''=\left( \frac{1}{1000}\ th\ parts \right)\] ![]()
The prefix “Centi” represents “one-hundredth parts”.
\[''centi''=\left( \frac{1}{100}\ th\ parts \right)\]
![]()
The prefix “Deci” indicates “one-tenth parts”.
\[''deci''=\left( \frac{1}{10}\ th\ parts \right)\]
![]()
The prefix “Deca” means “ten times”.
\[''deca''=\left( 10\ times \right)\]
![]()
The prefix “Hecto” implies “one hundred times”
\[''hecto''=\left( 100\ times \right)\]
![]()
The prefix “Kilo” refers to “one thousand times”
\[''kilo''=\left( 1000\ times \right)\]
![]()
What Do You Mean By “mg” Unit?
In the abbreviation “mg”, the first letter “m” implies “milli”, and the second letter “g” means “gram”.
Thus, “1mg” indicates “1 milligram”.
This “mg” unit finds useful when you want to measure some smaller portions of mass, like “1/1000th parts” of “1 gram”, or some smaller amount than it.
Thus, you have the following observation.
\begin{aligned}
1 \mathrm{mg} & =\frac{1}{1000} \text { th parts of } 1 \text { gram } \\
& =\frac{1}{1000} \times(1 \mathrm{gram}) \\
& =0.001 \mathrm{gram}
\end{aligned}
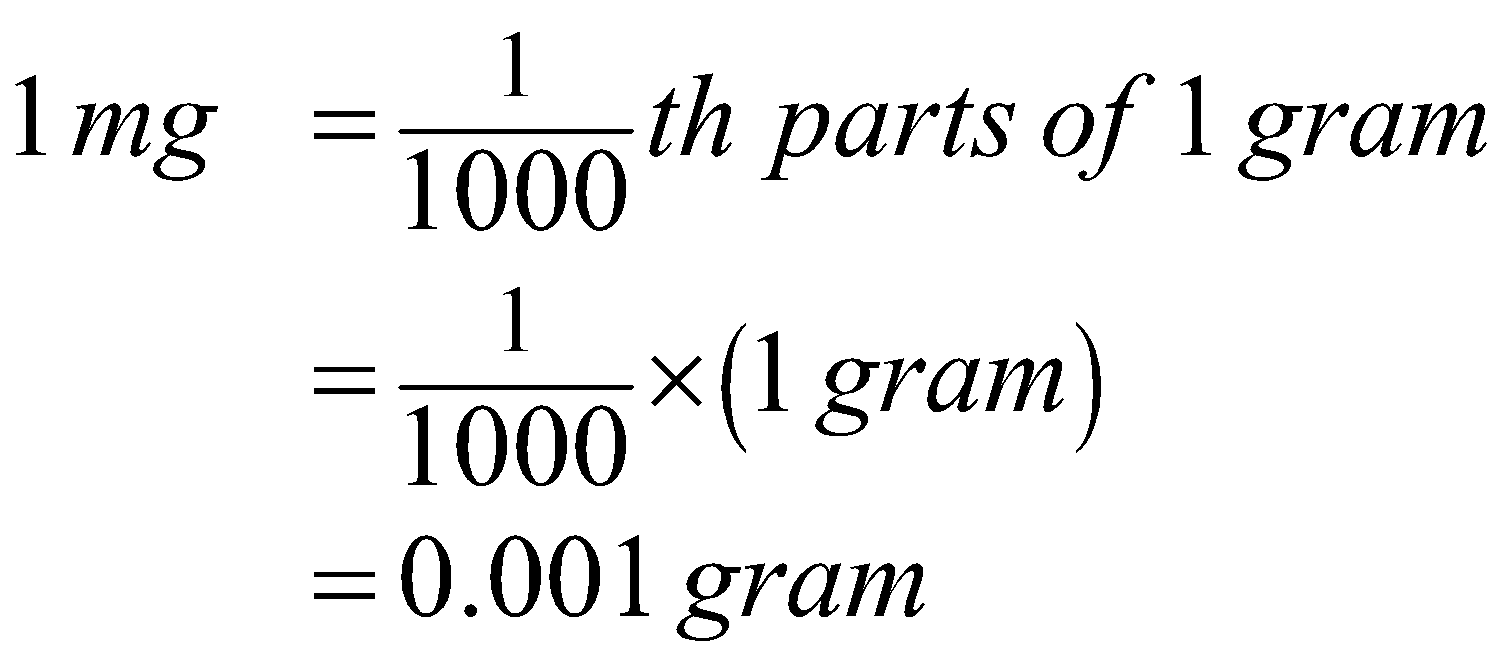
How many mg is there in “1 cg”?
In the abbreviation “cg”, the first letter “c” suggests “centi”, and the second letter “g” indicates “gram”.
Thus, “1cg” specifies “1centigram”.
Thus, you have the following observation.
\[1\ cg\quad =\ \frac{1}{100}\times \left( 1\ gram \right)\]
![]()
Also, you know the following.
\[1\ mg\quad =\ \frac{1}{1000}\times \left( 1\ gram \right)\]
![]()
Now, rewrite the “1 cg” in the following way.
\begin{aligned}
1 \mathrm{cg} & =\frac{1}{100} \times(1 \text { gram }) \\
& =\left[10 \times \frac{1}{1000}\right] \times(1 \text { gram }) \\
& =10 \times\left[\frac{1}{1000} \times(1 \text { gram })\right] \\
& =10 \times 1 \mathrm{mg} \\
& =10 \mathrm{mg}
\end{aligned}![]()
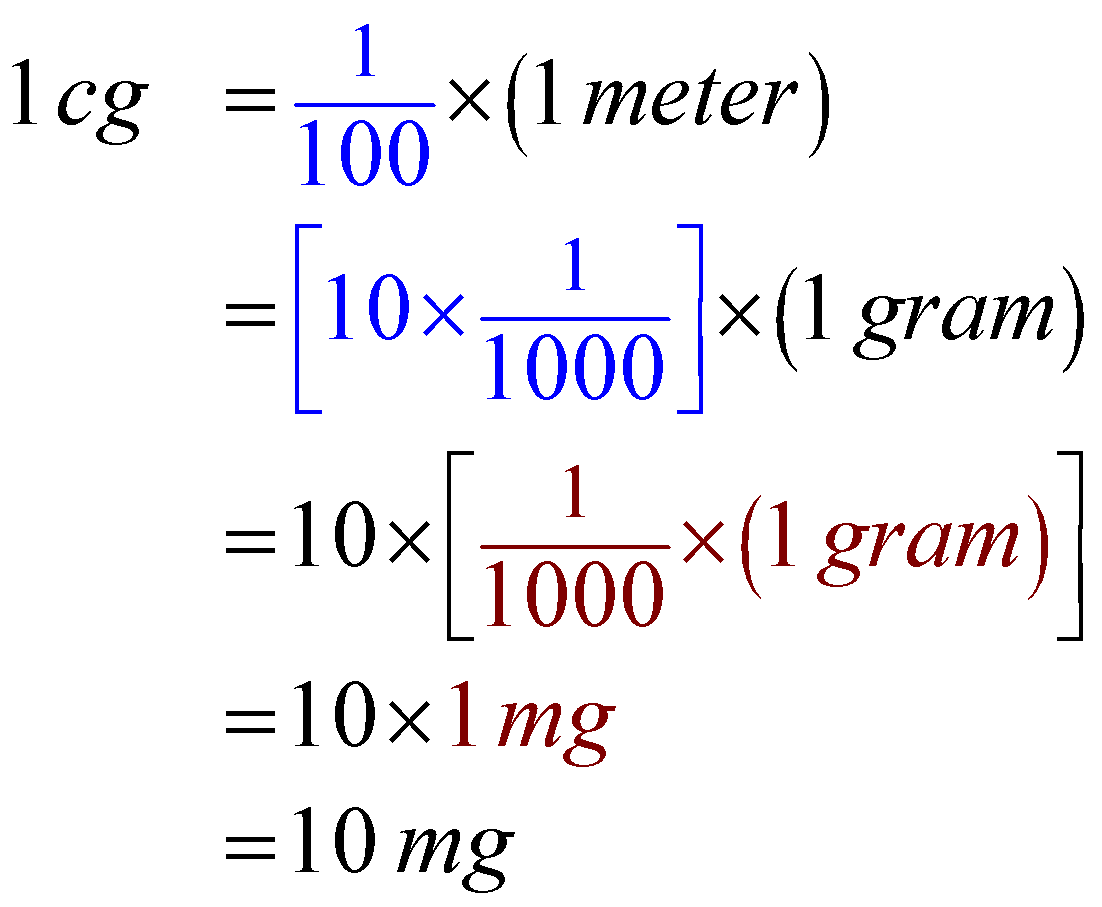
Thus, you have “10mg” in “1cg”.
How many mg is there in “1g”?
The fact is that when you apply the prefix “milli” in front of the unit “gram”, it implies the “one-thousand parts” of a “gram”.
Mathematically, you can equate the following.
\begin{array}{ll}
1 \mathrm{mg} & =\frac{1}{1000} \times(1 \mathrm{gram}) \\
(1 \mathrm{mg}) \times 1000 & =\frac{1}{1000} \times(1 \mathrm{gram}) \times 1000 \\
1000 \times 1 \mathrm{mg} & =\frac{1}{1000} \times 1000 \times 1 \mathrm{gram} \\
1000 \mathrm{mg} & =1 \text { gram }
\end{array}
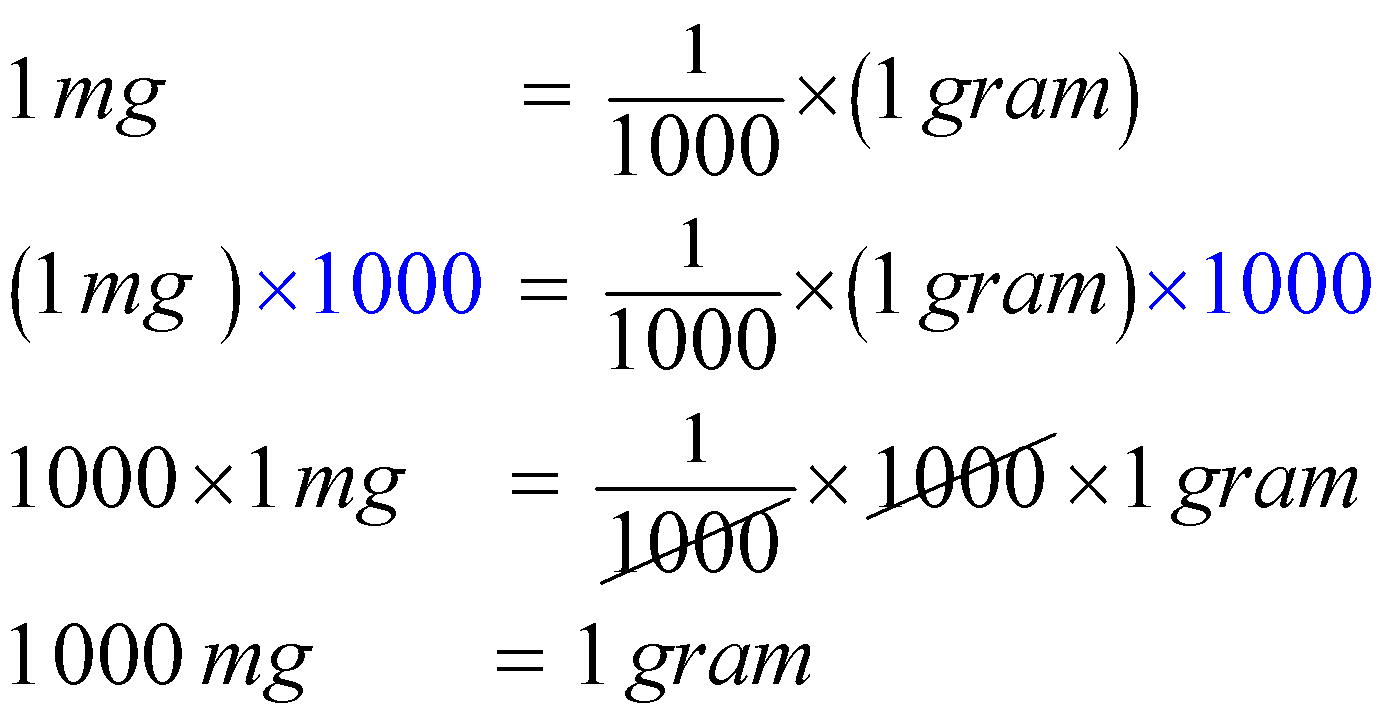
Thus, in “1g” there are “1000 mg”.
How many mg is there in “1kg”?
It is natural that adding the prefix “kilo” before the unit “gram”, will imply the “one-thousand times” of a “gram”.
Thus, you have the following observation.
\[1\ kg=\ \ 1000gram\]
![]()
Also, you know the following.
\[1\ mg\quad =\ \frac{1}{1000}\times \left( 1\ gram \right)\]
![]()
So, you can write the following mathematical equation.
\begin{aligned}
1 \mathrm{~kg} & =1000 \mathrm{gram} \\
& =1000 \times(1 \mathrm{gram}) \\
& =1000 \times\left(1000 \times \frac{1}{1000} \times 1 \text { gram }\right) \\
& =1000 \times 1000 \times\left(\frac{1}{1000} \times 1 \mathrm{gram}\right) \\
& =1000000 \times(1 \mathrm{mg}) \\
& =10,00,000 \mathrm{mg}
\end{aligned}
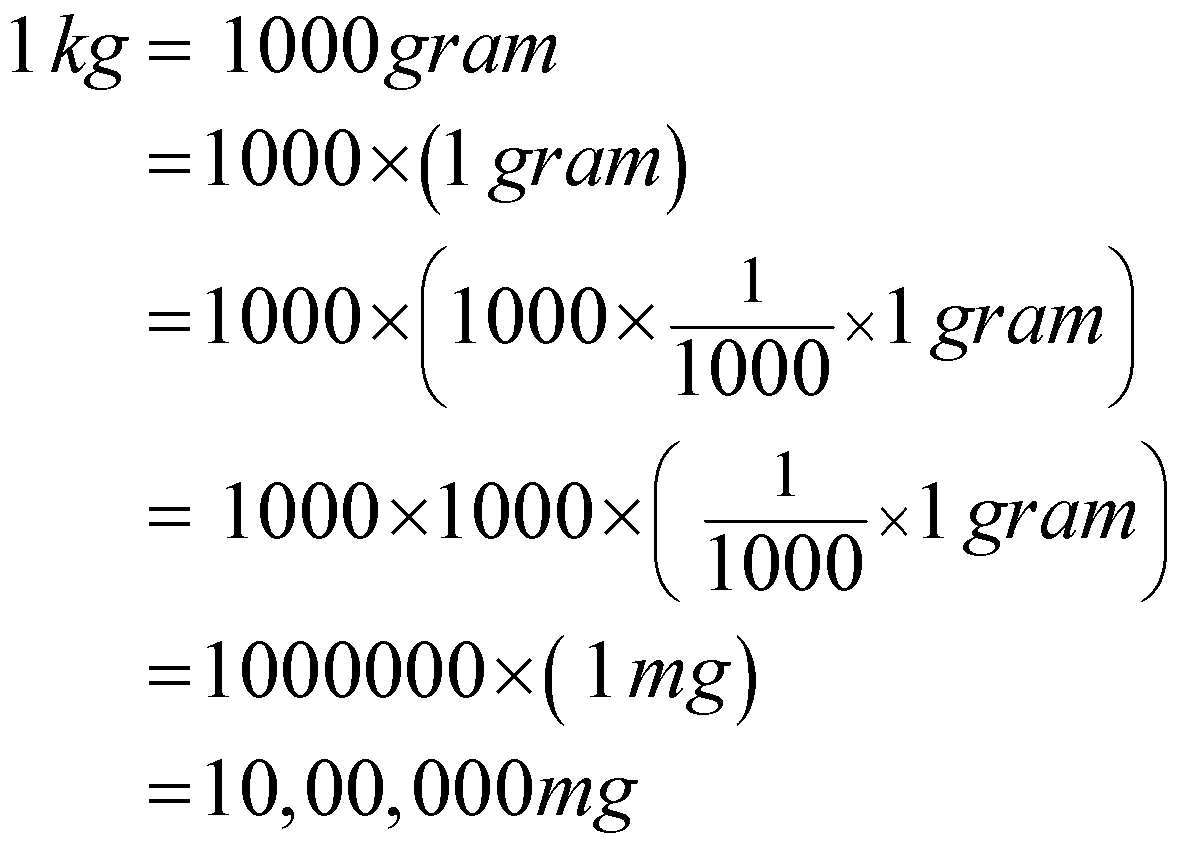
Hence, there are “10,00,000 mg” in “1kg”.
Frequently Asked Questions (FAQs)
Yes, utilizing the conversion formula \[1\ cg\ \ =\ \ \frac{1}{100}\times 1\ g\] ![]() , “1111cg” can be converted to the corresponding “gram” in the following way.
, “1111cg” can be converted to the corresponding “gram” in the following way.
\begin{aligned}
1 \mathrm{cg} & =\frac{1}{100} \times 1 \mathrm{~g} \\
\therefore 1111 \mathrm{cg} & =1111 \times\left[\frac{1}{100} \times 1 \mathrm{~g}\right] \\
& =\frac{1111}{100} \times 1 \mathrm{~g} \\
& =11.11 \mathrm{~g}
\end{aligned}
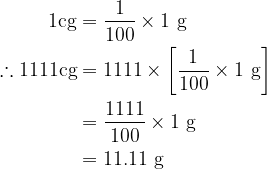
Thus, there are “11.11g” in “1111cg”.
The mass “6 gram” has no prefix before the unit “gram”.
\begin{aligned}
1 m g & =\frac{1}{1000} \times(1 g) \\
\therefore 6 g & =6 \times(1 \mathrm{~g}) \\
& =6 \times 1000 \mathrm{mg} \\
& =6000 \mathrm{mg}>6 \mathrm{mg}
\end{aligned}
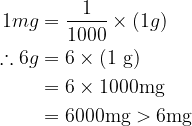
So, “6g” is, obviously, bigger than “6mg”.
Yes, employing the conversion formula \[1\ mg\ \ =\ \ \frac{1}{1000}\times 1\ g\] ![]() “5550mg”, can be converted to the corresponding “gram” in the following way.
“5550mg”, can be converted to the corresponding “gram” in the following way.
\begin{aligned}
1 \mathrm{mg} & =\frac{1}{1000} \times 1 \mathrm{~g} \\
\therefore 5550 \mathrm{mg} & =5550 \times\left\{\frac{1}{1000} \times 1 \mathrm{~g}\right\} \\
& =5550 \times \frac{1}{1000} \times 1 \mathrm{~g} \\
& =5.55 \mathrm{~g}
\end{aligned}
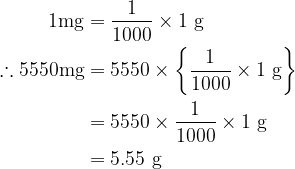
So, there are “5.55g” in “5550mg”.
Yes, using the conversion formula \[1\ mg\ \ =\ \ \frac{1}{1000}\times 1\ g\] ![]() , “55mg” can be converted to corresponding “g” in the following way.
, “55mg” can be converted to corresponding “g” in the following way.
\begin{aligned}
1 m g & =\frac{1}{1000} \times(1 g) \\
\therefore 55 m g & =55 \times(1 m g) \\
& =55 \times \frac{1}{1000} \times(1 \mathrm{~g}) \\
& =0.055 \mathrm{~g}
\end{aligned}
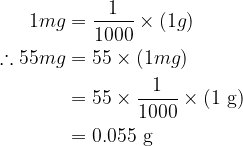
So, there are “0.055g” in “55mg”.
Yes, engaging the conversion formula, \[1\ mg\ \ =\ \ \frac{1}{1000}\times 1\ g\] ![]() , “10g” can be converted to corresponding “mg” in the following way.
, “10g” can be converted to corresponding “mg” in the following way.
\begin{aligned}
&
1 \text { gram }=1000 \mathrm{mg} \\
& \begin{aligned}
\therefore 10 \mathrm{~g} & =10 \times 1000 \times(1 \mathrm{mg}) \\
& =10 \times 1000 \mathrm{mg} \\
& =10000 \mathrm{mg}
\end{aligned}
\end{aligned}
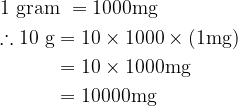
So, there are “10,000mg” in “10g”.
The mass “5cg” or “5 centigram” has the prefix “centi” before the unit “gram”.
\begin{aligned}
&
1 \mathrm{cg}=\frac{1}{100} \times(1 \mathrm{gram})=10 \mathrm{mg} \\
& \therefore 5 \mathrm{cg}=5 \times \frac{1}{100} \times(1 \mathrm{gram}) \\
& =5 \times 10 \mathrm{mg} \\
& =50 \mathrm{mg}>5 \mathrm{mg} \\
&
\end{aligned}
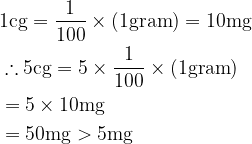
So, “5cg” is, obviously, greater than “5mg”.