PEMDAS Full Form
What is the full form of PEMDAS?
The full form of PEMDAS is Parenthesis, Exponents, Multiplication, Division, Addition, and Subtraction.
In this topic, we'll discuss the importance and order of operations in mathematics of the acronym PEMDAS. Besides, without the given guidelines the targeted nature of mathematical calculation could not exist. The complete form of PEMDAS is parenthesis, exponents, multiplication, division, addition, and subtraction. Moreover, the simplest way to memorize this acronym is the phrase “Please Excuse My Dear Aunt Sally”. We will understand it in detail in upcoming sections.
Furthermore, the calculations need to be done in the order provided, which means that we have to go first, second, third, then on until the calculation is complete. Besides, if there are grouping symbols within the expression then PEMDAS will tell you to calculate within the symbols first.
Importance of PEMDAS
For obtaining the right answer with the guidelines we need PEMDAS. For instance, calculate 3 × 4 + 9 so that to understand the answer we can first undertake multiplication and then add the numbers we get 12 + 9 = 21. Also, there's another way in which we add first and after that multiply the product 3 × 13 = 39.
Hence, the question here is in both the solutions which one is correct? The correct answer is one as it uses the PEMDAS.
PEMDAS Symbols
P is the first letter which means you have to first solve the calculation in a grouping.
After that, search for E that are exponents and ignore any other operation, and take the exponents to their powers.
The PEMDAS ‘M’ appears before ‘D’ but it doesn't mean that you have to multiply first and then divide you have to follow the order of questions here means from left to right whichever appears first.
A and S also have identical property means whichever appears first will be solved first.
Examples of PEMDAS
Let’s understand the PEMDAS by an example
Example -
Suppose you're told to simplify the following expression
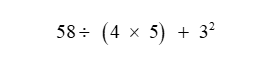
58 \div(4 \times 5)+3^2
Solution:
1st step:
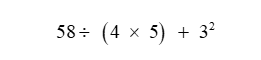
58 \div(4 \times 5)+3^2
2nd step:
=58 \div 20+3^2
3rd step:
=58 \div 20+9
4th step:
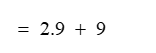
=2.9+9
5th Step:
=11.9
Therefore, 
58 \div(4 \times 5)+3^2=11.9
In this, We follow the PEMDAS and first searched for grouping symbols but there were none. Secondly, we glance for exponents, which we discover as 23 so we solved it.
Thirdly, I have taken M (multiplication) and D (division) from left to right, and after finding them we solve them. Finally, after solving multiplication and division we glance for addition ‘A’ and subtraction ‘S’ in the left to right order of whichever appears first.
Frequently Asked Questions (FAQs)
PEMDAS stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction.
Yes, if there is any operation is missing in the equation we can skip that and move further with the next operation.
The only difference between these two methods is, in BODMAS we use ‘division’ before ‘multiplication’ in an equation. While in PEMDAS, we use ‘multiplication’ before ‘division’ in an equation. However, PEMDAS is the synonym of BODMAS.
BODMAS is an acronym and it stands for Bracket, Order, Division, Multiplication, Addition, and Subtraction. In certain regions, PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction) is employed, which is the synonym of BODMAS.
We need to follow PEMDAS in order to get the correct answer. If we didn’t follow the PEMDAS in sequence order then the resulting solution will be wrong. As we follow the BODMAS rule same we need to follow the PEMDAS rule.