Acceleration Due To Gravity

Acceleration due to gravity, denoted as g, is a fundamental concept in physics that describes the acceleration of objects due to the gravitational pull of the Earth. This acceleration is approximately
9.8 m/s2 near the Earth's surface. It means that in the absence of air resistance, any object will increase its velocity by about 9.8m/s for every second it falls.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. What is Newton's Law of Gravitation?
2. Acceleration Due to Gravity
3. Solved Examples Based on Newton's Law of Gravitation
4. Summary

Understanding g is crucial for explaining various phenomena, from the simple act of dropping a stone to the complex orbits of satellites. Everyday experiences, such as the way objects fall to the ground or how projectiles move through the air, are governed by this constant. By exploring the principles of acceleration due to gravity, we can better grasp how gravity influences motion, ensuring we can predict and analyze the behaviour of objects under its influence. This article delves into the details of gravitational acceleration and also includes some solved examples based on this concept.

What is Newton's Law of Gravitation?

According to Newton's law of gravitation, the gravitational force is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.

Due to gravitational force, Each particle in this universe attracts every other particle.

The direction of this force is along the line joining the particles.

Let two particles of masses $m_1$ and $m_2$ separated by a distance r exert a Force F on each other. The magnitude of F is given as

$
F \propto \frac{m_1 m_2}{r^2}
$

Or,
$
F=\frac{G m_1 m_2}{r^2}
$

Where

$\begin{aligned} & F \rightarrow \text { Force } \\ & G \rightarrow \text { Gravitational constant } \\ & m_1, m_2 \rightarrow \text { Masses } \\ & r \rightarrow \text { Distance between masses }\end{aligned}$

Acceleration Due to Gravity

The Gravitational Force exerted by the earth on a body is known as the gravitational pull of gravity. And this force will produce an acceleration in the motion of a body. This is known as the acceleration due to gravity.

Variation in the Value of g Due to Shape of Earth

The value of acceleration due to gravity (g) changes its value due to the following factors

1. The shape of the earth

2. Height above the earth's surface

3. Depth below the earth's surface

4. Axial rotation of the earth.

Variation of 'g' Due to the Shape of the Earth

Earth has an elliptical shape as shown in Fig.

Where the Equatorial radius is about 21 km longer than the polar radius.

Or,

$R_c>R_p$

Variation in 'g' Due to Height

Let's study Variation in 'g' with height

Value of g at the surface of the earth (at distance r=R from earth centre)

$g=\frac{G M}{R^2}$

Value of g at height h from the surface of the earth (at a general distance r=R+h from earth centre)

$
g^{\prime} \alpha \frac{1}{r^2}
$

Where $r=R+h$

As we go above the surface of the earth, the value of g decreases

So, $g^{\prime}=\frac{G M}{r^2}$

Where gravity at a height h from the surface of the earth.

$R \rightarrow$ The radius of the earth
$h \rightarrow$ height above the surface

• Value of ' $g$ ' at $\infty$

if $r=\infty \quad g^{\prime}=0$

No effect of Earth's gravitational pull at infinite distances.

• Value of g when h < < R

• Formula

1. Value of g

$\begin{aligned} & g^{\prime}=g\left(\frac{R}{R+h}\right)^2=g\left(1+\frac{h}{R}\right)^{-2} \\ & g^{\prime}=g\left[1-\frac{2 h}{R}\right]\end{aligned}$

2. The absolute decrease in the value of g with height

$\Delta g=g-g^{\prime}=\frac{2 h g}{R}$

3. The fractional decrease in the value of g with height

$\frac{\Delta g}{g}=\frac{g-g^{\prime}}{g}=\frac{2 h}{R}$

4. Percentage decrease in the value of g with height

$\frac{\Delta g}{g} \times 100 \%=\frac{2 h}{R} \times 100 \%$

Where $R_e \rightarrow$ Radius of the equator
$R_p \rightarrow$ Radius of pole
So $g_p>g_e$
In fact $g_p=g_c+0.018 \mathrm{~m} / \mathrm{s}^2$

Or we can say Weight increases as the body is taken from the equator to the pole. This is denoted by g.

Let gravitational force exerted by the earth on the body of mass m resting on the surface of the earth is given by

$F=\frac{G M m}{R^2}$ …(1)

Where M = mass of the earth and R = radius of the earth

And If g is the acceleration due to gravity then this F can be written as

F=(mass)*(acceleration)=mg ...(2)

On Comparing

We get

$
g=\frac{G M}{R^2}
$

Now $\rho \rightarrow$ density of the earth
Then $M=\rho *\left(\frac{4}{3}\right) \pi R^3$
So $g=\frac{4}{3} \pi \rho G R$

• Its average value is $9.8 \mathrm{~m} / \mathrm{s}^2$ or $981 \mathrm{~cm} / \mathrm{sec}^2$ or $32 \mathrm{feet} / \mathrm{s}^2$ on the surface of earth.

• It is a vector quantity and its direction is always towards the centre of the earth/Planet.

• $\text { Dimension- } L T^{-2}$

• Its value depends upon the mass, radius, and density of the Earth/Planet.

This means Planet having more value of $\rho R$ than the earth will have a greater value of acceleration due to gravity (g) than the earth

$\begin{array}{rl}\quad & I f(\rho R)_P>(\rho R)_E \\ \mathrm{I} . \mathrm{e} & g g_P>g_E\end{array}$

• It is independent of the mass, shape and density of the body situated on the surface of the Earth/planet.

Value of g will be the same for a light as well as heavy body if both are situated on the surface of the Earth/planet.

Variation in 'g' Due to Depth

Let's study Variation in 'g' with depth

Value of g at the surface of the earth (at d=0)

$g=\frac{G M}{R^2}=\frac{4}{3} \pi \rho g R$

Value of g at depth d from the surface of the earth (at a general distance r=(R-d) from earth centre)=g'

And $g^{\prime} \propto(R-d)$

This means Value of g' decreases on going below the surface of the earth.

So $g^{\prime}=g\left[1-\frac{d}{R}\right]$

Value of 'g' at the centre of the earth

At the centre

depth from surface $(d)=R$
So $g^{\prime}=0$

i.e., Acceleration due to gravity at the centre of the earth becomes zero.

The absolute decrease in the value of g with depth

$\Delta g=g-g^{\prime}=\frac{d g}{R}$

The fractional decrease in the value of g with depth

$\frac{\Delta g}{g}=\frac{g-g^{\prime}}{g}=\frac{d}{R}$

The value of g decreases with depth.

Percentage decrease in the value of g with depth

$\frac{\Delta g}{g} \times 100 \%=\frac{d}{R} \times 100 \%$

Note- The rate of decrease of gravity outside the earth (h<<R) is double that of inside the earth.

Recommended Topic Video

Solved Examples Based on Newton's Law of Gravitation

Example 1: The weight of the object will be

1) more at the poles of the earth

2) more at the equator of the earth

3) same at the equator and poles of the earth

4) same everywhere on the earth

Solution:

Variation of 'g' due to the shape of the earth

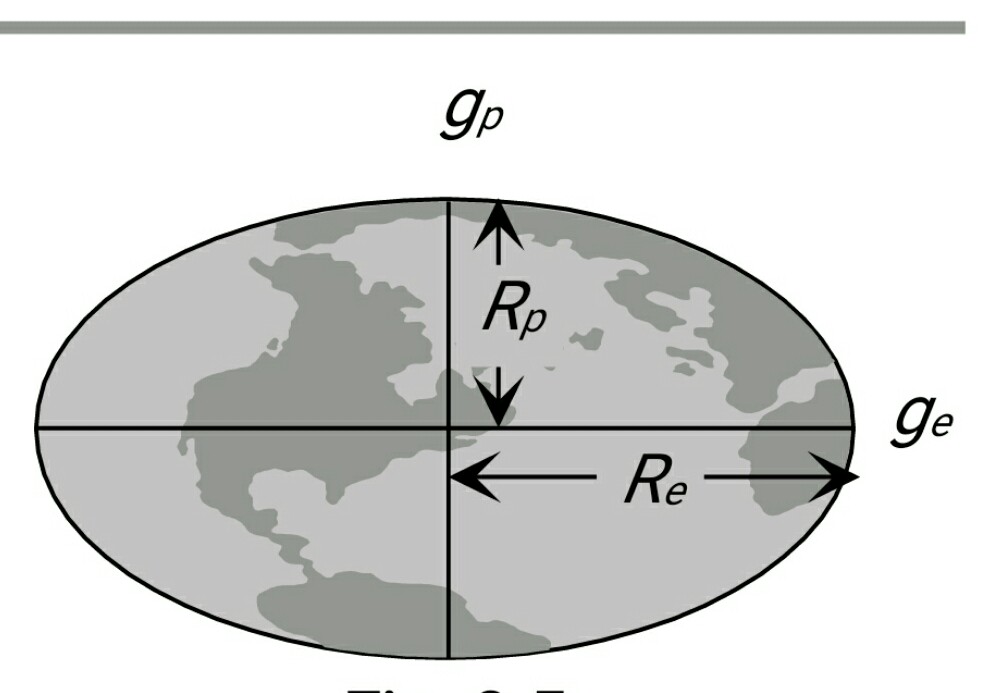
The Equatorial radius is about 21 km longer than the polar radius.

$
\begin{aligned}
& \mathrm{R}_{\text {equator }}>\mathrm{R}_{\text {pole }} \\
& R_e \rightarrow \text { Radius of equator } \\
& R_p \rightarrow \text { Radius of pole } \\
& \text { wherein } \\
& g_{\text {pole }}>g_{\text {equator }} \\
& g_p=g_e+0.018 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$

Weight increases as the body is taken from the equator to the pole
As we know,
$
g \propto \frac{1}{R^2}
$

Here, $R_c>R_p$ then $g_p>g_c$
$
g_p=g_e+0.018 \mathrm{~m} / \mathrm{s}^2
$

Hence weight at the poles is greater as compared to Earth's equator.

Example 2: Let $g_p$ and $g_e$ be the acceleration due to gravity on the Earth's pole and Earth's equator respectively, then which of the following is true?

1) $g_e>g_p$
2) $g_e=g_p$
3) weight decreases as the body is taken from the equator to the pole
4) $g_p>g_e$

Solution:

Variation of 'g' due to the shape of the earth

The Equatorial radius is about 21 km longer than the polar radius.

$R_{\text {equator }}>R_{\text {pole }}$
$R_e \rightarrow$ Radius of equator
$R_p \rightarrow$ Radius of pole
wherein
$g_{\text {pole }}>g_{\text {equator }}$
$
g_p=g_c+0.018 \mathrm{~m} / \mathrm{s}^2
$

Weight increases as the body is taken from the equator to the pole

Weight will increase as the body is taken from the equator to the pole

$
g_p=g_e+0.018 \mathrm{~m} / \mathrm{s}^2
$
so, $g_p>g_e$

Hence, the answer is option (4).

Example 3: What is the main reason for the variation in the value of 'g' due to the shape of the Earth?

1) Latitude of the place

2) Altitude of the site

3) Longitude of the place

4) None of the above

Solution:

The shape of the Earth is not perfectly spherical, but rather a flattened spheroid with a bulge at the equator and a flattening at the poles. This non-uniform shape of the Earth affects the value of 'g', which is the acceleration due to gravity at a particular location. At the equator, the centrifugal force due to the Earth's rotation cancels out some of the gravitational force, resulting in a lower 'g' value. There is no centrifugal force at the poles and the value of 'g' is higher. Therefore, the value of 'g' varies depending on the latitude of the location.

Hence, the answer is the option (1).

Example 4: In which of the following locations will the value of 'g' be highest?

1) Equator

2) Centre of earth

3) Pole

4) Tropic of Cancer

Solution:

Gravitational acceleration is highest at the poles and lowest at the equator due to the shape of the Earth. At the Poles, the gravitational force is at its maximum because, unlike at the equator, there is no centrifugal force to reduce it. Also, the Equatorial radius is about 21 km longer than the polar radius.

Hence, the answer is the option (3).

Example 5: Which of the following factors affects the value of 'g'?

1) Earth's mass

2) Distance from the centre of the Earth

3) The shape of the Earth

4) All of the above

Solution:

The value of 'g' is affected by many factors such as the mass of the earth, the distance from the centre of the earth, and the shape of the earth. The greater the mass of the Earth, the stronger the gravitational force and the higher the value of 'g'. Similarly, the closer the location is to the centre of the Earth, the stronger the gravitational force and the higher the value of 'g'. Finally, as mentioned earlier, the shape of the Earth, which is not perfectly spherical, affects the value of "g".

Hence, the answer is the option (4).

Summary

Acceleration due to gravity (g) is approximately 9.8 m/s2 near the Earth's surface, dictating how objects accelerate due to Earth's gravitational pull. This fundamental concept is essential for understanding the motion of falling objects and the orbits of celestial bodies. Newton's law of gravitation further explains that gravitational force is proportional to the product of two masses and inversely proportional to the square of their distance.