Accuracy Precision Error Measurement

Q: Write the type of precision?

Repeatability It is defined as The variation in measurement that occurs when the same person measures the same quantity many times. This measurement is performed by using the same equipment and procedure. Reproducibility It is defined as The variations in measurement when a quantity is measured by different individuals and the person measures the same part several times with the help of the same equipment.

Q: Differentiate between accuracy and precision in measurement?

Accuracy Precision It is termed as the degree of conformity It is termed to be as the degree of relatability Accuracy is defined as the difference between the mean value of a particular performed experiment or experimental value of the measurement and the True value of that measurement that is used to calculate a result of a given experiment. Precision is defined as a quantity in measurement that shows how closely two or many measurements of the same quantity are in terms of one another. The value of accuracy can be found out by one measurement It needs different measurements

Accuracy Precision Error Measurement

Edited By Team Careers360 | Updated on Jul 02, 2025 05:09 PM IST

Measurement is defined as the most important thing that we can apply in science as well as mathematics. But when we are talking about measurement and they occur, some of the accurate measurements and some of the errors also occur in the measurement that is termed as precision. Even if we want to compare any weight or anything else such as the quantity we use the term such as measurement. But every measurement is not accurate. It carries some of the accuracies in it and that is termed as the error in the measurement.

This Story also Contains

Define error
Types of Error:
What is Accuracy

Accuracy Precision Error Measurement

Define error

Error is the difference between the measured value and the actual value.

For example, if we want to calculate the value of quantity by the instrument or the device and it is done by two operators then it is not necessary that both operators give the same result. The difference between the two measurements that are taken by the two different operators is termed to be an error.

Types of Error:

1. Gross error :

It is a kind of error that occurs due to the mistake that is made by humans by breeding and recording the instrument. This is the most common error that occurs during any kind of measurement if we are using any kind of titration then it may be possible then we are not using the buret in a proper way so the gross error occurs. To avoid gross errors you must take proper care regarding the data.

2. Random errors :

As the name suggests these errors occur in a random way not because due to any proper condition these are termed to be random errors. These types of errors can arise due to unpredictable changes in the temperature and the voltage supplied during an experiment.

3. Systematic error:

These types of errors are further classified into three different groups :

Environmental Errors: Environmental errors are those errors that are affected by the external conditions of the environment on the measurement. This type of error occurred due to external conditions such as changes in temperature and pressure.

Observational Error: when the experiment is not set up with the proper care and the Observer is doing carelessness in such a type of condition observation error occurs.

Instrumental Errors: This type of error arises due to the wrong calibration of the measuring instrument. When the equipment used is faulty then changes in the reading may occur and the zero error is a very common type of error that occurs in the instrumental errors.

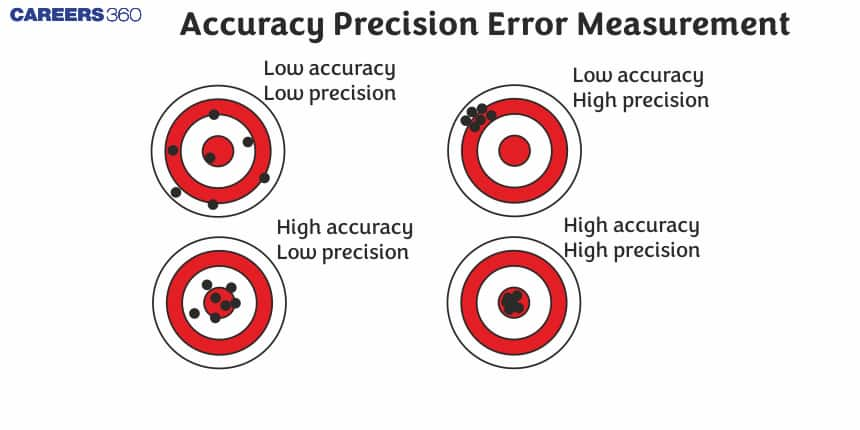
What is Accuracy

Accuracy is defined as the difference between the mean value of a particular performed experiment or experimental value of the measurement and the True value of that measurement that is used to calculate a result of a given experiment. Another meaning of accuracy is to find true value.

So mathematically it can be written as,

Accuracy = Mean value - True value.

When we talk about accuracy we find out that the difference between the mean value and true is much smaller than the accuracy is found to be much larger in an experimental result.

Example of Accurate vale :

We have been given a compound that contains 50g of nitrogen mean value. Now you are advised to perform two different experiments and find out the concentration of the Iron elements that are present in the compound.

You find out that through method A the true concentration of iron is found to be 20g and in experiment B the true concentration is found to be 10hg.

Solution:

Accuracy = Mean value - True value

Method A = 50g - 20g = 30g

Method B = 50g - 10g = 40g

Define Precision

Precision is defined as a quantity in measurement that shows how closely two or many measurements of the same quantity are in terms of one another. It is calculated by finding out the difference between a measured value and the arithmetic mean value for many different measurements.

Mathematically it can be written as

Precision = Individual Value – Arithmetic Mean

Example of Precision

As a result we find out the extent of agreement between the repeated measurements that have been provided for the same quantity. It is observed that if the difference between the individual values of repeated measurements is smaller, the precision is greater.

We are taking an example to understand the concept of concept is

A speedometer given. Let us first consider that Car A runs at 50km/hr. If the speedometer which you are using for the purpose of measuring speed shows the value of 48.8 or 48.9 or 49 then the measurements of these types are considered precise but not accurate. Now if the speedometer shows 49.7 or 50.5 then these values will be considered accurate but not precise.

Frequently Asked Questions (FAQs)

1. What are absolute errors?

Absolute errors are defined as those errors in which the variation occurs between the actual value and the measured value.

Absolute error = |VA -VE |

2. Write the type of precision?

Repeatability

It is defined as The variation in measurement that occurs when the same person measures the same quantity many times. This measurement is performed by using the same equipment and procedure.

Reproducibility

It is defined as The variations in measurement when a quantity is measured by different individuals and the person measures the same part several times with the help of the same equipment.

3. Write the name of accuracy.

Point accuracy

Accuracy of Percentage on uniform scale

Accuracy when defined as Percentage of True Value

4. Differentiate between accuracy and precision in measurement?

Accuracy	Precision
It is termed as the degree of conformity	It is termed to be as the degree of relatability
Accuracy is defined as the difference between the mean value of a particular performed experiment or experimental value of the measurement and the True value of that measurement that is used to calculate a result of a given experiment.	Precision is defined as a quantity in measurement that shows how closely two or many measurements of the same quantity are in terms of one another.
The value of accuracy can be found out by one measurement	It needs different measurements

5. What is the concept of "error bars" in graphical representations of data?

Error bars are graphical representations of the variability of data. They indicate the uncertainty in a reported measurement. On a graph, they extend from each data point, showing the range within which the true value is likely to fall, based on the measurement's uncertainty.

6. What is the concept of "measurement uncertainty" and how is it different from error?

Measurement uncertainty quantifies doubt about the measurement result. It's an estimate of a range of values that is likely to include the true value. Error, on the other hand, is the difference between a measured value and the true value. Uncertainty acknowledges that the true value is unknown.

7. How does the concept of "tolerance" relate to measurement accuracy?

Tolerance is the permissible deviation from a specified value. It defines the acceptable range of variation in a measurement or manufactured part. While related to accuracy, tolerance is more about defining acceptable limits rather than the closeness to the true value.

8. How does hysteresis affect measurement accuracy?

Hysteresis is the dependence of a system's output on its history of inputs. In measurements, it can cause different readings when approaching a value from different directions. This can introduce errors and affect accuracy, particularly in mechanical or magnetic measuring devices.

9. How does the concept of "outliers" relate to measurement accuracy and precision?

Outliers are data points that significantly differ from other observations. They can affect both accuracy and precision. Outliers may indicate a genuine extreme value, a measurement error, or a problem with the measurement process. Proper handling of outliers is crucial for maintaining data integrity.

10. How does systematic error differ from random error?

Systematic errors are consistent, repeatable deviations from the true value, often due to faulty equipment or flawed methodology. Random errors are unpredictable fluctuations in measurements due to various uncontrollable factors. Systematic errors affect accuracy, while random errors affect precision.

11. What is the difference between absolute and relative error?

Absolute error is the difference between the measured value and the actual value, expressed in the same units as the measurement. Relative error is the absolute error divided by the actual value, often expressed as a percentage. Relative error allows for comparison between measurements of different magnitudes.

12. What is meant by "propagation of errors" in calculations?

Propagation of errors refers to how uncertainties in individual measurements combine to affect the uncertainty of a calculated result. When performing calculations with measured values, the uncertainties in each measurement contribute to the overall uncertainty of the final result.

13. What is the importance of reporting uncertainties with measurements?

Reporting uncertainties with measurements is crucial because it provides information about the reliability and limitations of the data. It allows others to assess the quality of the measurements, make informed decisions based on the data, and properly compare results from different experiments or sources.

14. What is the relationship between resolution and precision in measurements?

Resolution refers to the smallest change in a quantity that an instrument can detect. While high resolution can contribute to precision, they are not the same. An instrument with high resolution allows for more precise measurements, but other factors like random errors also affect overall precision.

15. What's the difference between accuracy and precision in measurements?

Accuracy refers to how close a measurement is to the true value, while precision refers to how consistent or reproducible measurements are. An accurate measurement is close to the actual value, whereas precise measurements are close to each other but not necessarily to the true value.

16. Can a measurement be precise but not accurate?

Yes, a measurement can be precise but not accurate. This occurs when repeated measurements are consistent with each other (high precision) but are systematically off from the true value (low accuracy). For example, if a scale consistently measures 1 kg too high, it's precise but not accurate.

17. How does rounding affect the accuracy and precision of a measurement?

Rounding can affect both accuracy and precision. Excessive rounding can reduce accuracy by moving the value further from the true value. It also reduces precision by limiting the number of significant figures, potentially obscuring small but important variations in measurements.

18. How does calibration relate to accuracy in measurements?

Calibration is the process of adjusting an instrument to provide results that are accurate compared to a known standard. Regular calibration helps maintain accuracy by correcting for systematic errors that may develop over time due to wear, environmental factors, or other influences.

19. How does the concept of uncertainty relate to measurements?

Uncertainty in measurements represents the range within which the true value is likely to fall. It acknowledges that no measurement is perfect and quantifies the doubt about the result. Uncertainty is often expressed as a range (±) or a percentage.

20. What is meant by "significant figures" in a measurement?

Significant figures are the digits in a measurement that are known with certainty, plus one estimated digit. They indicate the precision of a measurement. For example, 12.34 cm has four significant figures, implying precision to the nearest 0.01 cm.

21. How do significant figures relate to the precision of a measurement?

Significant figures indicate the precision of a measurement. The number of significant figures reflects how precisely the measurement was made. For example, 1.00 cm (three significant figures) implies a more precise measurement than 1 cm (one significant figure).

22. What is meant by "least count" in measurements?

The least count of a measuring instrument is the smallest division that can be measured accurately with that instrument. It represents the resolution of the instrument. For example, a ruler with millimeter markings has a least count of 1 mm.

23. What is meant by "precision to tolerance ratio" in measurements?

The precision to tolerance ratio (P/T ratio) is a measure of the capability of a measurement system relative to the tolerance of the part being measured. A lower P/T ratio indicates a more capable measurement system. Generally, a P/T ratio of 0.1 or less is considered good.

24. How does the concept of "significant digits" differ from "decimal places"?

Significant digits include all certain digits plus one uncertain digit, regardless of decimal point position. Decimal places only count digits to the right of the decimal point. For example, 0.00230 has two decimal places but three significant digits.

25. What is the importance of traceability in measurements?

Traceability in measurements refers to the ability to relate a measurement to a national or international standard through an unbroken chain of comparisons. It ensures that measurements are consistent and comparable across different times, places, and laboratories.

26. What is the significance of "confidence interval" in measurements?

A confidence interval provides a range of values that is likely to contain the true value with a certain level of confidence. It quantifies the reliability of an estimate. For example, a 95% confidence interval means there's a 95% probability that the true value lies within that range.

27. What is the concept of "measurement linearity" and why is it important?

Measurement linearity refers to how consistently a measuring instrument's output changes in proportion to changes in the input. Good linearity means the instrument responds uniformly across its range, which is crucial for accurate measurements over a wide range of values.

28. What is the importance of "measurement traceability" in scientific experiments?

Measurement traceability ensures that measurements can be related to reference standards through an unbroken chain of comparisons. This is crucial for scientific experiments as it allows results to be reliably compared across different labs, times, and locations, enhancing reproducibility and credibility.

29. How does the concept of "sensitivity" relate to measurement accuracy?

Sensitivity in measurements refers to the smallest change in the measured quantity that can be detected by the measuring instrument. High sensitivity allows for detection of small changes, potentially improving accuracy. However, high sensitivity can also make an instrument more susceptible to noise and fluctuations.

30. What is the importance of "measurement system analysis" in ensuring accuracy and precision?

Measurement system analysis (MSA) is a set of methods used to assess the capability of a measurement system. It helps identify sources of variation in the measurement process, including equipment, operators, and methods. MSA is crucial for ensuring that measurements are both accurate and precise.

31. How does the concept of "guard banding" relate to measurement accuracy and tolerance?

Guard banding is a practice of narrowing the acceptable range of measurements to account for measurement uncertainty. It ensures that accepted measurements are more likely to be truly within tolerance, improving the reliability of quality control processes.

32. What is the significance of "measurement resolution" in digital instruments?

Measurement resolution in digital instruments is the smallest change in input that produces a detectable change in the displayed output. While high resolution can allow for more precise readings, it's important to remember that resolution doesn't necessarily equate to accuracy or overall measurement uncertainty.

33. What is the importance of "measurement traceability chain" in ensuring accuracy across different labs or countries?

The measurement traceability chain is the sequence of measurements and calibrations that relates a measurement result to established standards, usually national or international standards. It ensures that measurements made in different locations or times are comparable and consistent, which is crucial for scientific collaboration and international trade.

34. How does the choice of measuring instrument affect accuracy and precision?

The choice of measuring instrument directly impacts both accuracy and precision. More sophisticated instruments generally offer higher accuracy and precision. For example, a digital caliper typically provides more accurate and precise measurements than a standard ruler.

35. How does temperature affect measurement accuracy?

Temperature can affect measurement accuracy in several ways. It can cause thermal expansion or contraction of the measuring instrument or the object being measured. Some instruments may be calibrated for specific temperatures, and using them outside this range can introduce errors.

36. What is the difference between accuracy and trueness?

While often used interchangeably, accuracy and trueness have distinct meanings in metrology. Trueness refers to the closeness of the average of a large number of measurements to the true value, while accuracy encompasses both trueness and precision.

37. How does parallax error affect measurements?

Parallax error occurs when the observer's line of sight is not perpendicular to the scale of the measuring instrument. This can lead to inaccurate readings. To minimize parallax error, always ensure your eye is directly in line with the measurement point.

38. How does sample size affect the accuracy and precision of measurements?

Increasing sample size generally improves both accuracy and precision. With a larger sample, random errors tend to average out, improving precision. It also provides a better estimate of the true value, enhancing accuracy. However, it doesn't eliminate systematic errors.

39. What is the difference between repeatability and reproducibility in measurements?

Repeatability refers to the variation in measurements taken by a single person or instrument under the same conditions. Reproducibility refers to the variation in measurements made by different people or instruments, or under different conditions. Both contribute to overall precision.

40. What is meant by "measurement bias"?

Measurement bias is a systematic error that causes measurements to consistently deviate from the true value in a particular direction. It affects the accuracy of measurements and can be due to factors like improper calibration, consistent misreading, or flawed methodology.

41. How does the concept of "uncertainty budget" relate to measurement accuracy?

An uncertainty budget is a comprehensive list of all sources of uncertainty in a measurement process. It helps in understanding and quantifying the overall uncertainty in a measurement result, allowing for a more accurate assessment of the measurement's reliability.

42. How does digital resolution affect measurement accuracy?

Digital resolution, the smallest increment a digital instrument can display, can affect perceived accuracy. While high resolution allows for finer measurements, it doesn't necessarily improve accuracy. The last digit may imply more precision than the instrument actually provides.

43. How does the choice of reference point affect measurement accuracy?

The choice of reference point can significantly impact measurement accuracy. An inappropriate or unstable reference point can introduce systematic errors. For example, measuring the height of a mountain using sea level as a reference point requires accounting for tidal variations.

44. How does the concept of "drift" affect long-term measurement accuracy?

Drift refers to a gradual, unintended change in instrument readings over time. It can be caused by factors like component aging or environmental changes. Drift affects long-term accuracy and necessitates regular calibration to maintain measurement reliability.

45. What is meant by "measurement resolution" and how does it differ from accuracy?

Measurement resolution is the smallest change in the measured quantity that causes a perceptible change in the corresponding indication. While high resolution allows for finer measurements, it doesn't guarantee accuracy. An instrument can have high resolution but poor accuracy due to calibration issues.

46. What is meant by "measurement range" and how does it affect accuracy?

Measurement range is the span between the minimum and maximum values that an instrument can measure. Using an instrument within its specified range is crucial for accuracy. Measurements at the extremes of the range may be less accurate due to non-linearity or other factors.

47. How does the concept of "repeatability" differ from "reproducibility" in measurements?

Repeatability refers to the closeness of agreement between successive measurements of the same quantity under the same conditions. Reproducibility, on the other hand, refers to the closeness of agreement between measurements of the same quantity under changed conditions, such as different operators or instruments.

48. What is the significance of "calibration curves" in improving measurement accuracy?

Calibration curves establish the relationship between the instrument's response and known standard values. They help correct for systematic errors and non-linearity in the instrument's response. Using calibration curves can significantly improve measurement accuracy across the instrument's range.

49. How does the concept of "measurement stability" relate to long-term accuracy?

Measurement stability refers to the ability of a measuring instrument to maintain its metrological characteristics over time. Good stability ensures that measurements remain accurate over extended periods. Factors affecting stability include environmental conditions, wear and tear, and internal component drift.

50. What is meant by "measurement noise" and how does it affect precision?

Measurement noise refers to random fluctuations in the measured signal that are not part of the true value. It can be caused by various factors such as electronic noise, environmental disturbances, or limitations of the measuring system. Noise directly affects precision by introducing variability in repeated measurements.

51. How does the concept of "measurement accuracy ratio" relate to instrument selection?

The measurement accuracy ratio is the ratio of the measurement process accuracy to the tolerance of the characteristic being measured. A higher ratio indicates a more capable measurement system relative to the required tolerance. It's a crucial factor in selecting appropriate measuring instruments for specific tasks.

52. How does the concept of "measurement uncertainty budget" contribute to understanding overall accuracy?

A measurement uncertainty budget is a detailed breakdown of all sources of uncertainty in a measurement. It includes factors like instrument accuracy, environmental effects, and operator variability. By quantifying each source, it provides a comprehensive understanding of the overall measurement uncertainty.

53. What is meant by "type A" and "type B" uncertainties in measurements?

Type A uncertainties are those evaluated by statistical methods, typically from repeated measurements. Type B uncertainties are evaluated by other means, such as manufacturer specifications, calibration certificates, or expert judgment. Both types contribute to the overall measurement uncertainty.

54. How does the concept of "measurement accuracy class" relate to instrument selection?

Measurement accuracy class is a standardized way of expressing the accuracy of measuring instruments. It typically indicates the maximum permissible error as a percentage of the full scale or measured value. Understanding accuracy classes helps in selecting appropriate instruments for specific measurement tasks.