Ampere - Definition, Formula, Symbol, Conversion FAQs

What is Ampere?

The ampere is the fundamental unit of electric flow. It is commonly abbreviated as "amp". Ampere is named after André-Marie Ampère (1775–1836), the father of electrodynamics.

By measuring the electromagnetic power between electrical conductors that transport the electric flow, the International System of Units characterises one-ampere in terms of other base units. An ampere is also called an amp.

The previous CGS estimation framework included two different definitions of current, one that was nearly identical to the SI units and the other that used electric charge as the basis unit, with the unit of charge defined by estimating the power between two charged metal plates. The ampere is defined as 1 coulomb of charge per second at the time. The coulomb, a SI unit of charge, is defined as the charge carried by one-ampere electric current for one second.

On and after May 20, 2019, new definitions for invariant constants of nature, specifically the primitive charge, will be declared public and used.

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

Define 1 Ampere

One ampere is equal to the rate of flow of charge of one coulomb in one second. 1 Ampere definition is "Ampere is that constant current which, if maintained in two straight parallel wires of infinite length, insignificant circular cross-section as well as placed one meter apart in vacuum, would produce a force equal to $2 \times 10^{-7} \mathrm{~N} / \mathrm{m}$ of length between these conductors." An ampere is a unit of electric current.

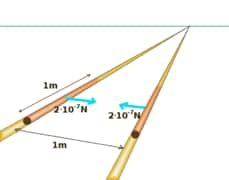
1 Ampere Is Equal To

Between two parallel wires transmitting an electric flow, there is an attracting or repulsive force, according to Ampère's force law. The ampere's formal meaning makes use of this power. The Coulomb is defined as "the amount of power delivered in 1 second by a current of 1 ampere watt" by the International System of Units. A current of one ampere is equal to, one coulomb of passing through a specific place every second: charge Q is usually determined by a steady current I flowing for a time t, as $Q = It$.

The charge amassed, or neglected, across a circuit is transmitted in coulombs, while the consistent, instantaneous, and usual current is given in amperes as in "charging current is $1.2 A$"The ampere's $(\mathrm{C} / \mathrm{s})$ relationship to the coulomb is the same as the watt's $(\mathrm{J} / \mathrm{s})$ connection to the joule.

Ampere Unit in CGS and MKS System of Units

In the centimetre–gram–second (CGS) system of units, the ampere was originally defined as one-tenth of a unit of electric flow. The ampere, as it is today known, was defined as the unit of current that produces a power of two dynes for every centimetre of length between two wires separated by one centimetre. The unit's length was chosen such that the units obtained from it in the MKSA framework could be usefully estimated. The "global ampere," defined as the present that could store $0.001118$ grams of silver every second from a silver nitrate setup, was an early recognition of the ampere.

Following it, more exact calculations revealed that the current is $0.99985 A$.

Ampere Formula

1. Ohm's Law Relation

Current is the ratio of voltage to resistance:

$
I=\frac{V}{R}
$

So,

$
1 \mathrm{~A}=\frac{1 \mathrm{~V}}{1 \Omega}
$

2. Charge-Current Relation

Current is the rate of flow of charge:

$
I=\frac{Q}{t}
$

Thus,

$
1 \mathrm{~A}=\frac{1 \mathrm{C}}{1 \mathrm{~s}}
$

3. Power Relation (already given)

$
\begin{aligned}
I & =\frac{P}{V} \\
1 \mathrm{~A} & =\frac{1 \mathrm{~W}}{1 \mathrm{~V}}
\end{aligned}
$

What Is An Ammeter?

An ammeter (short for ampere meter) is a measuring device used to determine the current in a circuit. The name comes from the fact that electric flows are measured in amperes (A). Milliammeters and microammeters are terms for instruments that measure small fluxes in the milliampere or microampere range. Early ammeters were research equipment whose activity was based on the Earth's attractive field. Improved instruments, which could be put in any position and allowed precise calculations in electric power frameworks, were developed by the late nineteenth century.

Symbol of Ammeter

The symbol of the ampere is the capital letter $\mathrm{A}$.

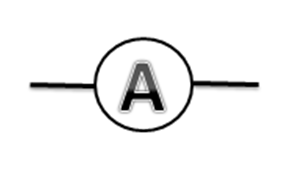
Ammeters have a very low resistance to current flow, and they are always connected in a circuit. An ammeter (short for ampere meter) is a measuring device used to determine the current in a circuit. The name comes from the fact that electric flows are measured in amperes (A). Milliammeters and microammeters are terms for instruments that measure small fluxes in the milliampere or microampere range.

Conversion of amps to milliamps

$1 \mathrm{~A}=1000 \mathrm{~mA}$

Conversion of milliamps to amps

1 milli ampere equals to 0.001 amps

$1 \mathrm{~mA}=10^{-3} \mathrm{~A}$

Conversion of microamps to amps

1 microampere is equal to 0.000001 ampere

$ 1 \mu A=10^{-6}$ $(\mathrm{A})$

What is The Definition of Ampacity?

Ampacity is the maximum amount of electric current that a wire or cable can safely carry without overheating or causing damage.

• It depends on the wire’s material, size (cross-sectional area), and insulation.
• Higher ampacity means the wire can carry more current safely.
• If current exceeds the ampacity, the wire can overheat, melt, or cause fire hazards.

Also, check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

Formulae Involving Ampere

1. Ohm's Law

$I=\frac{V}{R}$

where,

• $I$ is the current (in ampere)
• $V$ is the voltage ( in volts)
• $R$ is the resistance ( in ohms)

2. Power

$P=I \times V$

where,

• $P$ is the power (in watts)
• $I$ is the current ( in ampere)
• $V$ is the voltage (in volts)

3. Joule's Law

The equation for Joule's law is given as:

$H=I^2 R t$

where,

• $H$ is the heat ( in joules)
• $I$ is the current ( in ampere)
• $R$ is the resistance ( in volts)
• $T$ is time ( in seconds)

4. Ampere's Law

The equation for Ampere's law is:

$B=\frac{\mu_0 I}{2 \pi r}$

where,

• $B$ is the magnetic field (in Teslas)
• $I$ is the current ( in ampere)
• $r$ is the distance

5. Equation Relating Current and Charge

$I=\frac{Q}{t}$

where,

• $I$ is the current ( in ampere)
• $Q$ is the electric charge ( in coulombs)
• $t$ is the time ( in seconds)

Also See,