Angular Acceleration - Definition, Formula, Angular Acceleration Formula

Angular acceleration is a basic concept in rotational motion. It is the rate of change of angular velocity with respect to time. Angular acceleration also helps to control the movement of a rotational body. In this article, we understand the angular acceleration definition, angular acceleration formula, angular acceleration units, and dimensional formula. It also includes the concept of some important terms related to angular acceleration and the relation between linear and angular acceleration. It can also be applied from various household appliances to vehicles.

This Story also Contains

1. What Is Angular Acceleration?/ Define Angular Acceleration
2. Angular Acceleration Units
3. Angular Acceleration Equation
4. Relation Between Angular Acceleration And Linear Acceleration
5. Angular Velocity And Angular Acceleration
6. Equations Of Motion In Rotational Motion
7. Applications Of Angular Acceleration
8. Some Important Terms Related to Angular Acceleration

What Is Angular Acceleration?/ Define Angular Acceleration

Angular acceleration is defined as the rate of change of angular velocity.

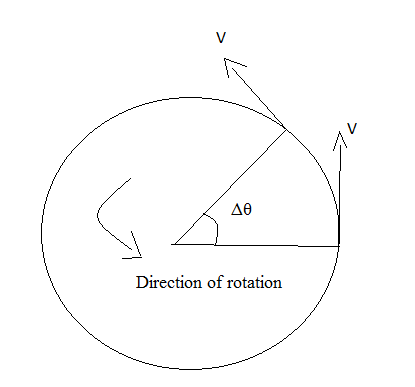
The angular acceleration is denoted by the symbol $\alpha$. The formula for angular acceleration is,

$\mathrm{\alpha}=\frac{\mathrm{d} \omega } {\mathrm{dt}}$

Here, $\omega$ is the angular velocity changing with time t.

Angular Acceleration Units

The unit of angular acceleration is measured as a change in angle per unit time squared.

• SI unit of angular acceleration: Radians per squared second
• Dimension of angular acceleration: $\left[\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^{-2}\right]$

Angular acceleration is also known as rotational acceleration. Similar to angular velocity, the direction of angular acceleration is also perpendicular to the plane of rotation. It also directs away from the viewer if the object is moving clockwise and directs towards him if the object is moving anti-clockwise.

Angular Acceleration Equation

As mentioned above the angular acceleration is given by, $\mathrm{\alpha}=\frac{\mathrm{d} \omega } {\mathrm{dt}}$

For a finite change, $\alpha=\Delta \omega / \Delta t$

Then the angular acceleration equation is written as, $\alpha=\frac{\omega_2-\omega_1 }{ t_2-t_1}$

Here, $\omega_1$ and $\omega_2$ are the initial and final angular velocities; $t_1$ and $t_2$ are the initial and final time.

Relation Between Angular Acceleration And Linear Acceleration

According to one-dimensional kinematics, linear acceleration is represented by,

$a_{\mathrm{t}}=\frac{\Delta v }{ \Delta t}$ ……………………………………......................... (1)

Here, $v$ is the velocity changing with time $t$.

In rotational motion, velocity $v=r \omega$…………………...... (2)

Here, $r$ is the radius of the circle and $\omega$ is the angular velocity.

Substituting equation (2) in equation (1) then,

$a_t=\frac{\Delta(r \omega) }{ \Delta t}$ ……………………………………………..….. (3)

We know that for a circular motion, the radius is constant. Hence,

$\Delta(\mathrm{r} \omega)=\mathrm{r}(\Delta \omega)$ ………………………………...……….. (4)

we get,

Linear acceleration, $\mathrm{a}_{\mathrm{t}}=\frac{\mathrm{r} \Delta \omega }{ \Delta \mathrm{t}}$ ..………………………… (5)

Angular acceleration is defined as the rate of change of angular velocity.

Therefore,$\alpha=\frac{\Delta \omega }{ \Delta t}$ ………………………………………. (6)

On comparing equations (5) and (6) we obtain,

$a_t=r \alpha$

Or, angular acceleration $\alpha=\frac{a_t }{ r}$

Thus, angular acceleration is inversely proportional to the radius of the circle.

Angular Velocity And Angular Acceleration

Angular velocity is applicable in determining the rotation of a body concerning the inertial frame of reference. To determine the rate of change of angular velocity and to depict the direction of the change, angular acceleration is used.

Equations Of Motion In Rotational Motion

An object moving with a rotational motion under constant acceleration measures the angular velocity of the object with the help of equations called kinematic equations. The equations are,

$\omega_{\mathrm{f}}=\omega_{\mathrm{i}}+\alpha \mathrm{t}$

$\theta=\omega_i t+0.5 \alpha t^2$

$\omega_{\mathrm{f}}^2=\omega_{\mathrm{i}}^2+2 \alpha(\theta)$

Factors Affecting Angular Acceleration

• Torque: Angular acceleration increases with an increase in torque. It also affects the direction of angular acceleration.
• Moment of inertia: As moment of inertia increases, angular acceleration decreases.
• Frictional forces can reduce angular acceleration as they oppose the motion of the body.

Applications Of Angular Acceleration

1. Amusement park rides

In Ferris wheels, there is a sudden change in rotational speed resulting in high acceleration which gives a sense of weightlessness.

2. Washing machine

The drum in the washing machine is subjected to high angular acceleration which helps to separate water from clothes.

3. Ballet

In ballet, performers control angular acceleration for a speedy smooth spin.

Some Important Terms Related to Angular Acceleration

1. Angular velocity:

If an object rotates around a centre point in a particular given time t, then the velocity of the object is defined as the angular velocity. It is also termed as the rate of change of angle θ with time t. The symbol of angular velocity is omega ($\omega$).

Therefore, angular velocity, $\omega=\frac{d \theta}{ d t}$

Unit of angular velocity: Radian per second

Angular velocity has SI units as $1 / \mathrm{s}^2$ or $\mathrm{s}^{-1}$

Angular velocity explains the speed at which the object rotates and gives the direction of the rotating object. The direction of angular velocity is perpendicular to the plane of rotation. The angular velocity directs away from us if the object is moving clockwise while it directs toward us if the object is moving anti-clockwise.

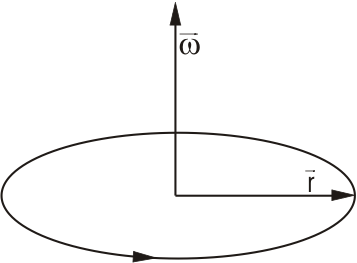
Figure 1 Representation of the direction of angular velocity ω with the radius of circle r

Suppose an object moves in a circle with constant speed, the motion of the object is said to be a uniform circular motion. Then the object has constant angular velocity in a uniform circular motion.

2. Average angular velocity: This is obtained by dividing angular displacement by the time taken for displacement.

3. Angular force

If the object is rotating along a curved path, the force acting on that object is called angular force.

The angular force formula is given by, $\tau=I \alpha$

4. Omega

Omega is defined as the symbolic representation of angular velocity. It is represented as radian per second.

We know that, $\omega=2 \pi f$

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects