Banking of Roads - Meaning, Formula, FAQs

When we are in a car or even on a bicycle, our speed tends to decrease just as we near a corner, this happens because as we turn, the likelihood of our tires slipping increases with vehicle speed hence the need to slowly down; hence the adaptation of brake pads that adjusts speed. It is noticeable that, anytime it rains, you are forced to decelerate while going around a corner than under normal circumstances; this is due to a decrease in frictional force assisting in making turns.

This Story also Contains

1. What Is Banking of Roads?
2. Illustration of Banked Road
3. Frictionless Banking of Road Derivation
4. Angle Of Banking Derivation (Without Friction)
5. Banking Of Road With Friction
6. Forces Related To Banking Of Roads
7. Necessity of Banking
8. Limitations Of Banking
9. Solved Examples Based on Banking of Roads

In this article, we will cover the concept of banking on the roads Physics class 11 which comes under under the chapter Laws of Motion. It is essential for board exams and also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of two questions have been asked on this concept. And for NEET one questions were asked from this concept.

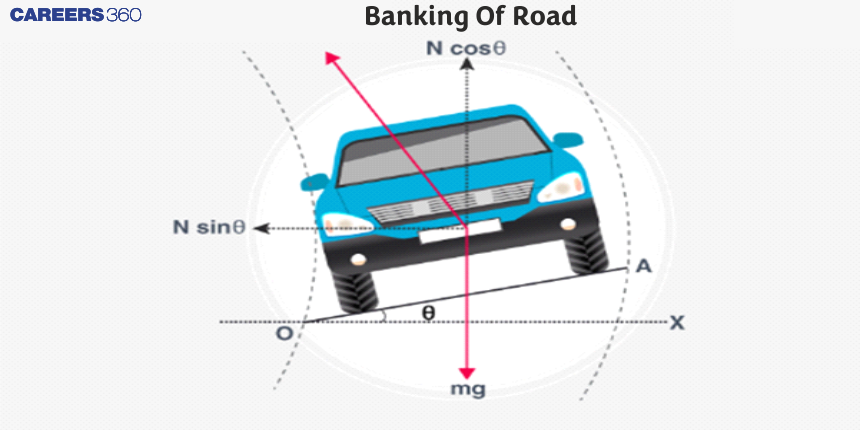
What Is Banking of Roads?

Banking of road definition: It is the phenomenon in which the outer borders of the curved roads banked are raised above the inner edge to provide the necessary centripetal force to the cars for them to make a safe turn.

Illustration of Banked Road

The outer border of a road is pushed up such that it is higher than the inner edge during a turn, and the road's surface seems to be a slightly inclined plane. This is referred to as road banking. The banking angle is the angle formed by the surface with the horizontal, i.e. the angle of inclination. When driving down such a curvy road, it's important to keep your eyes on the road.

There is a horizontal component to the normal force pressing on the vehicle. This component produces the centripetal force required to keep the vehicle from skidding.

Frictionless Banking of Road Derivation

The vertical component of the road's normal force on a vehicle balances its weight in the absence of friction, while the horizontal component provides the centripetal force towards the road's center of curvature. The applied load N on a body of mass m traveling with velocity v along a curved road with a banking angle formula can be split into two perpendicular components.

The weight $mg$ is balanced by the vertical component $N_{vertical}$ of $N$. (g is the gravitational acceleration).

$\mathrm{N_{vertical} } = \mathrm{mg}$

$\mathrm{Ncosθ }= \mathrm{mg} (1)$

The centripetal force is provided by the horizontal component $N_{horizontal}$ of $N$. If $r$ is the radius of curvature,

$Horizontal =Fc$

$
N \sin \theta=m v^2 / r .
$........(2)

Equation (2) is divided by (1),

$v=\sqrt{g * r *(\tan \theta)}$

This is the greatest velocity at which an object can remain in a curved path.

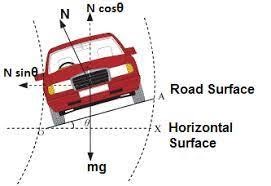
Angle Of Banking Derivation (Without Friction)

From figure,

$\begin{aligned}
&R \cos \theta=m g .... (i)\\
&\begin{aligned}
& R \sin \theta=\frac{m v^2}{r} ... (ii)\\
& \tan \theta=\frac{v^2}{r g} \\
& \tan \theta=\frac{\omega^2 r}{g}=\frac{V \omega}{g}=\frac{h}{l}
\end{aligned}
\end{aligned}$

Angle of Banking

$\theta=\tan ^{-1}\left(\frac{v^2}{r g}\right)$

$\mathrm{h}=$ height of outer edge from the ground level
$l=$ width of the road
$\mathrm{r}=$ radius

Banking Of Road With Friction

$
\frac{V^2}{r g}=\frac{\mu+\tan \theta}{1-\mu \tan \theta}
$

Where $\theta=$ angle of banking
$\mu=$ coefficient of friction
$V=$ velocity

• Maximum speed on a banked frictional road

$V=\sqrt{\frac{r g(\mu+\tan \theta)}{1-\mu \tan \theta}}$

Zero Banking Angle

A vehicle must turn on a flat surface if the banking angle is zero. Because the normal force is vertical and balances the vehicle's weight, it can no longer contribute to the centripetal force. There is no way to turn if the surface is smooth. The friction force can only provide the centripetal force on a rough surface. The forces' vertical components counterbalance each other.

Forces Related To Banking Of Roads

(i) Frictional Force

For the vehicle to keep moving in a circular path there is a force that acts between the tires of the vehicle and the road surface. This force is called the frictional force of banking roads. The frictional force in the banking of curved roads ensures the safe turning of the vehicle on curved paths and turns. Frictional force can be expressed in general as

$$f=\mu N$$

(ii) Normal Force

The perpendicular force supporting the vehicle's weight on a banked road is called normal force. The normal force has two components:

• The vertical component balances the weight

The equation for the vertical component: $N \cos \theta$

• The horizontal component contributes the required centripetal force for turning

The equation for the horizontal component: $N \sin \theta$

(iii) Centripetal Force

It is the force that causes angular or circular motion by pulling or pushing an object toward the center of a circle as it travels.

Another phrase used is banked turn, which is described as a turn or direction change in which the vehicle inclines towards the inside. The bank angle is the angle at which the vehicle is inclined. At the longitudinal and horizontal axes, there is an inclination. The equation for centripetal force on a banked road;

$F_c=N \sin \theta=\frac{m v^2}{r}$

Necessity of Banking

1. Banking is a technique for giving a vehicle the necessary centripetal force to make a safe turn on a curved route.

2. Skidding can be avoided by banking.

3. Overturning or toppling is less likely when roads are banked.

Limitations Of Banking

1. Bankng of curves needs more space which makes it difficult in urban areas.

2. Heavy vehicles need more friction than banking can provide thus making it less effective.

3. Constructing banked roads is more expensive compared to flat roads.

Recommended Topic Video

Solved Examples Based on Banking of Roads

Example 1: A circular road of radius 30 m has banking at an angle of $45^{\circ}$. The maximum safe speed of the car (in $\mathrm{m} / \mathrm{s}$ ) having a mass of 1000 kg will be if the coefficient of friction between tire and tire is $0.5\left[g=10 \mathrm{~m} / \mathrm{s}^2\right]$

1) 30

2) 20

3) 35

4) 45

Solution :

Maximum speed on a banked frictional road

$
V=\sqrt{\frac{r g(\mu+\tan \theta)}{1-\mu \tan \theta}}
$
maximum speed with the banked road with the friction is
$
\begin{aligned}
& v^2=r g\left[\frac{\mu+\tan \theta}{1-\mu \tan \theta}\right]=900 \mathrm{~m} / \mathrm{s} \\
\Rightarrow & v=30 \mathrm{~m} / \mathrm{s}
\end{aligned}
$

Hence, the answer is option (1).

Example 2: Statement I: A cyclist is moving on an unbanked road with a speed of -1 7 km-1 and takes a sharp circular turn along the path of a radius of 2m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve ( g= 9.8 m/s²)

Statement II: If the road is banked at an angle of $45^{\circ}$, the cyclist will not slip and pass the curve of a $2 \mathrm{~m}$ radius with a speed of $18.5 \mathrm{~km}-1$ without slipping.

1) Statement I is correct and Statement II is incorrect.

2) Both statement I and statement II are false.

3) Both statement I and statement II are true.

4) Statement I is incorrect and statement II is correct.

Solution :

$\begin{aligned}
V_{\max } & =\sqrt{\mu \mathrm{rg}}=\sqrt{(0.2) \times 2 \times 9.8} \\
\mathrm{~V}_{\max } & =1.97 \mathrm{~m} / \mathrm{s}=7.12 \mathrm{~km} / \mathrm{h}
\end{aligned}$

A cyclist is moving on an unbanked road with a speed of 7 km/h

$\text { Speed is lower than } V_{\max } \text {, hence it can take a safe turn. }$

Since the cyclist is riding at a safer speed of 7km/h, Statement I is correct.

For statement II

$\begin{aligned}
& \mathrm{V}_{\max }=\sqrt{\mathrm{rg}\left[\frac{\tan \theta+\mu}{1-\mu \tan \theta}\right]}=\sqrt{2 \times 9.8\left[\frac{1+0.2}{1-0.2}\right]} \\
& \mathrm{V}_{\max }=5.42 \mathrm{~m} / \mathrm{s}=19.5 \mathrm{~km} / \mathrm{h} \\
& V_{\min }=\sqrt{\frac{r g(\mu-\tan \theta)}{1+\mu \tan \theta}} \\
& \mathrm{V}_{\min }=3.615 \mathrm{~m} / \mathrm{s}=13.01 \mathrm{~km} / \mathrm{h}
\end{aligned}$

The speed of the cyclist is $18.5 \mathrm{~km} / \mathrm{h}=5.14 \mathrm{~m} / \mathrm{s}$

The sa peed of a cyclist is between the safe limit of $V_{\min }$ and $V_{\max }$, Statement II is also correct.

So, both statement I and statement II are true.

Hence, the answer is the option(3).

Example 3: A turn of radius 20 m is banked for the vehicle going to a speed of $5 \mathrm{~m} / \mathrm{s}$ If the width of a road is 8 m then what should be the height (in m ) of the outer edge w.r.t inner edge of the road.

1) 1

2) 0.5

3) 0.75

4) 0.25

Solution :

From figure,

$
\begin{aligned}
& N \sin \theta=\frac{m v^2}{R} \\
& N \cos \theta=m g \\
& \tan \theta=\frac{v^2}{R g}
\end{aligned}
$

For small angle $\theta \quad \tan \theta \approx \sin \theta \approx \frac{h}{l}$
$
\begin{aligned}
& \frac{h}{l}=\frac{v^2}{R g} \Rightarrow=\frac{5 \times 5}{20 \times 10} \\
& \frac{h}{l}=\frac{1}{8} \\
& \Rightarrow h=l / 8 \Rightarrow 8 / 8=1 \mathrm{~m}
\end{aligned}
$

Hence, the answer is option (1).

Example 4: The normal reaction ' $\mathrm{N}$ ' for a vehicle of $800 \mathrm{~kg}$ mass, negotiating a turn on a $30^{\circ}$ banked road at maximum possible speed without skidding is ____ $\qquad$ $\times 10^3 \mathrm{~kg} \mathrm{~m} / \mathrm{s}^2$

1) 10.2

2) 7.2

3) 12.4

4) 6.96

Solution:

For maximum possible speed, $\mathrm{f}_{\mathrm{s}}$ will be equal to $\mathrm{f}_{\mathrm{L} \text { i.e. }} \mathrm{f}_{\mathrm{L}}=\mu \mathrm{N}$
Along X-axis: $N \cos \theta=m g+f_L \sin \theta \rightarrow$ (1)
Along Y-axis: $f_L \cos \theta+N \sin \theta=\frac{m v_{\max }^2}{R} \rightarrow 2$
From Eqn (1)
$
N \cos \theta=m g+\mu N \sin \theta
$

$\begin{aligned}
& \mu=0.2 \\
& N \cos \theta=\mathrm{mg}+(0.2) N \sin \theta \\
& \theta=30^{\circ} \\
& N\left[\cos 30^{\circ}-0.2 \sin 30^{\circ}\right]=\mathrm{mg} \\
& N=\frac{800 \times 10}{\left[\frac{\sqrt{3}}{2}-0.2 \times \frac{1}{2}\right]}=\frac{800 \times 10}{(0.866-0.1)} \\
& \quad=\frac{8000}{0.766} \simeq 10.2 \times 10^3
\end{aligned}$

Hence, the answer is option (1).

Example 5: A car of mass 2000kg going round a banked curved a radius 40m on a frictionless road. If the banking angle is 45⁰, the speed of the car is :

1) 10m/s

2) 15m/s

3) 20m/s

4) 25m/s

Solution:

Banking of Road -

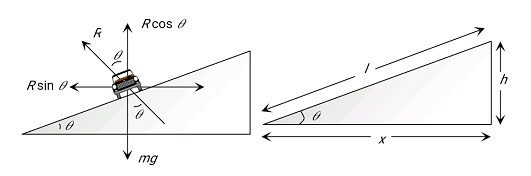
From figure

$\begin{aligned}
& R \cos \theta=m g ....(i)\\
& R \sin \theta=\frac{m v^2}{r}.....(ii) \\
& \tan \theta=\frac{v^2}{r g} \\
& \tan \theta=\frac{\omega^2 r}{g}=\frac{V \omega}{g}=\frac{h}{l}
\end{aligned}$

$\begin{aligned}
& \mathrm{h}=\text { highest of the outer edge } \\
& l \text { =length of rod } \\
& \mathrm{r}=\text { radius } \\
& \tan \theta=\frac{v^2}{r g} \\
& v=\sqrt{r g \tan \theta}=\sqrt{40 \times 10 \times \tan 45^{\circ}}=20 \mathrm{~m} / \mathrm{s}
\end{aligned}$

Hence, the answer is option (3).

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects