Bernoulli's Principle - Definition, Principle, Application, Limitations, FAQs

Bernoulli's Theorem, a principle in fluid dynamics, explains the relationship between pressure, velocity, and potential energy in a moving fluid. Formulated by Swiss mathematician Daniel Bernoulli, it states that as the speed of a fluid increases, its pressure decreases, and vice versa. This concept is fundamental in various real-world applications. For instance, in aviation, Bernoulli's principle helps explain how aeroplanes generate lift, allowing them to fly. Similarly, it's observed in the functioning of a carburettor in engines, where the flow of air and fuel is controlled to optimize combustion. Even in nature, the behaviour of water flowing through a pipe or wind moving through buildings follows this principle, making Bernoulli’s Theorem essential to understanding many aspects of both engineering and daily life.

What is Bernoulli’s Theorem and State Bernoulli’s Theorem or State and Prove Bernoulli’s Theorem

According to Bernoulli's principle, an increase in a fluid's speed is characterized by a reduction in static pressure or a decrease in the fluid's potential energy.
The principle was first stated in 1738 by Daniel Bernoulli in his book Hydrodynamic. Although Bernoulli deduced that pressure decreases as flow speed increases, it was Leonhard Euler who first put Bernoulli equation in its current form in 1752. The theory only applies to isentropic flows, in which the impacts of irreversible processes such as turbulence and non-adiabatic processes such as heat radiation are minor and may be ignored.

The assumption of conservation of energy can be used to derive Bernoulli's principle formula. In a continuous influx, the aggregate of all sources of energy in a fluid anywhere along the flow path is the same across all points along that flow path. For this to happen, the sum of kinetic energy, potential energy, and internal energy must remain constant.

Bernoulli's principle can be applied to a variety of fluid flows, yielding a number of different Bernoulli's equations. For incompressible flows, Bernoulli's equation in its simplest version is valid. Most liquids and gases, for example, move with a low Mach number. At increasing Mach numbers, more complex forms can be applied to compressible flows.

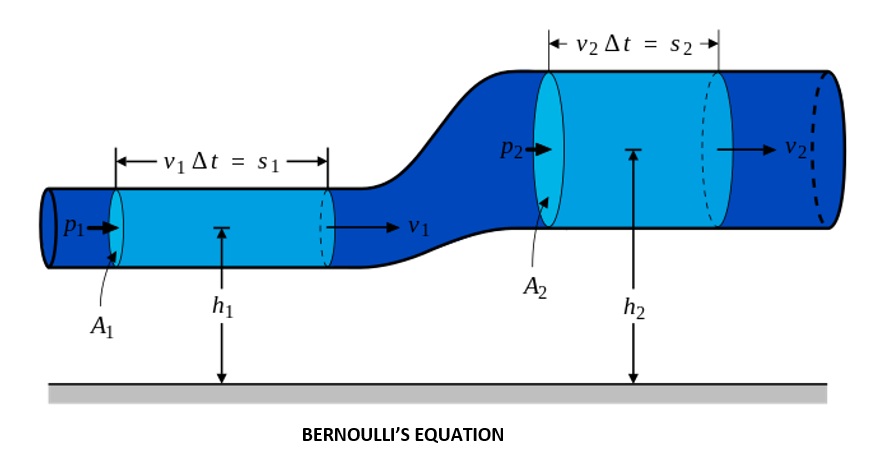
Principle of Conservation of Energy

Since energy cannot be generated or destroyed, it can be converted into another form. The principle of energy conservation is what this is characterized as. This principle is the basis for Bernoulli’s theorem. According to the principle of conservation of energy, the total energy at any point remains constant. There are three different forms of energy.

• Potential energy
• Pressure energy
• Kinetic energy

Potential Energy

The energy a fluid possesses due to its position above or below a datum line:

$$
\text { Potential Energy }=W \cdot h=m g h=m g Z
$$

Where:
- $h$ or $Z$ : Height of the fluid particle above the datum line (in meters)
- $m$ : Mass of the fluid (in kg )
- $W=m g$ : Weight of the fluid (in N )
- $g$ : Acceleration due to gravity (in $\mathrm{m} / \mathrm{s}^2$ )

Potential Energy per unit mass:

$$
\frac{\text { Potential Energy }}{m}=g Z \quad(\text { in } \mathrm{J} / \mathrm{kg})
$$

Pressure Energy

The energy a fluid possesses due to its pressure:
Pressure Energy $=P \cdot U$
Where:
- $P$ : Pressure of the fluid (in $\mathrm{N} / \mathrm{m}^2$ )
- $U$ : Specific volume of the fluid (in $\mathrm{m}^3 / \mathrm{kg}$ )

If $U=1$, then:

$$
\text { Pressure Energy }=P \quad(\text { in } \mathrm{J} / \mathrm{kg})
$$

Kinetic Energy

The energy of the fluid by virtue of its velocity is called kinetic energy.

$$
\text { Kinetic Energy }=\frac{1}{2} m V^2
$$

Where $m$ is the mass of the fluid $(\mathrm{kg})$ and $V$ is the velocity of the fluid $(\mathrm{m} / \mathrm{s})$.
Kinetic Energy per unit mass (specific energy):

$$
\frac{\text { Kinetic Energy }}{m}=\frac{V^2}{2}
$$

Total Energy of the Fluid (according to the principle of conservation of energy):
Total Energy = Potential Energy + Kinetic Energy + Pressure Energy

Substituting each term:

$$
\text { Total Energy }=g Z+\frac{V^2}{2}+\frac{P}{\rho}
$$

Dividing the total energy by $g$ to express in terms of total head:

$$
\text { Total Head or Total Energy }=Z+\frac{V^2}{2 g}+\frac{P}{\rho g}
$$

Alternatively, using specific weight $(w=\rho g)$ :

Total Head or Total Energy $=Z+\frac{V^2}{2 g}+\frac{P}{w}$
Bernoulli's Equation:
Since the total head remains constant:

$$
Z_1+\frac{V_1^2}{2 g}+\frac{P_1}{w}=Z_2+\frac{V_2^2}{2 g}+\frac{P_2}{w}
$$

Where:
- $Z_1, Z_2$ : Elevation head at points 1 and 2
- $\frac{V_1^2}{2 g}, \frac{V_2^2}{2 g}$ : Velocity head at points 1 and 2
- $\frac{P_1}{w}, \frac{P_2}{w}$ : Pressure head at points 1 and 2

This is the complete expression for Bernoulli’s equation.

Application of Bernoulli’s Theorem

• If the characteristics of the fluid flow in the region of the foil is known, Bernoulli's principle can be used to determine the lift force on an airfoil.
• Bernoulli's principle states that if air flowing past the top surface of an aircraft wing moves faster than air flowing past the bottom surface, the pressure on the wing's surfaces will be lower above than below. As a result of the pressure differential, a lifting force is generated upwards.
• Bernoulli's equations can be used to compute the lift forces (to a decent approximation) if the speed distribution past a wing's top and bottom surfaces is known.
• A device such as a Venturimeter or an orifice plate, which may be put into a pipeline to reduce the diameter of the flow, can be used to measure the flow speed of a fluid. The continuity equation for a horizontal device illustrates that for an incompressible fluid, a reduction in diameter causes an increase in fluid flow speed.
• Bernoulli's principle therefore demonstrates that in the lower diameter region, there must be a decrease in pressure. The Venturi effect is the term for this phenomenon.
• The nozzle of a Bunsen burner generates gas at a high velocity. As a result, the force within the burner's stem will decrease. As a result, air from the environment enters the burner.
• Bernoulli's theorem governs the operation of aeroplanes. The plane's wings have a certain form. When the plane is flying, the air flows across it at a high rate, although the plane's low surface wig. There is a differential in the flow of air above and below the wings due to Bernoulli's principle. As a result of the flow of air on the wings up surface, this phenomenon produces a decrease in pressure. If the force is greater than the plane's mass, the plane will ascend.

Limitations of Bernoulli’s Theorem

• Because of friction, the fluid particle velocity in the middle of a tube is the highest and gradually decreases in the tube's direction. As a result, because the particles of the liquid velocity are not consistent, the liquid's mean velocity must be used.
• This equation can be used to improve the efficiency of a liquid supply. It is ineffective in turbulent or non-steady flows.
• In an unstable flow, a tiny amount of kinetic energy can be converted to thermal energy, and in a thick flow, some energy can be lost due to shear stress. As a result, these setbacks must be ignored.
• The viscous action must be kept to a minimum level.
• The liquid flow will be controlled by the liquid's external force.
• This theorem is usually applied to fluids with low viscosity.
• Incompressible fluid is required.
• When a fluid is travelling in a curved path, the energy generated by centrifugal forces must be taken into consideration.
• The liquid flow should remain constant over time.

Bernoulli’s Theorem Proof

Starting with Euler's Equation of Motion:

$$
d P+V d V+g d Z=0
$$

Where:
- $d P$ : Change in pressure
- $V d V$ : Change in kinetic energy
- $g d Z$ : Change in potential energy

Step 1: Integration of Euler's Equation
Integrating along the streamline:

$$
\int d P+\int V d V+\int g d Z=\text { constant }
$$

This simplifies to:

$$
P+\frac{V^2}{2}+g Z=\text { constant }
$$

Where:
- $\quad P$ : Pressure energy per unit volume
- $\frac{V^2}{2}$ : Kinetic energy per unit volume
- $g Z$ : Potential energy per unit volume

Step 2: Dividing by $g$ to Express in Terms of Total Head
Divide the equation by $g$ :

$$
\frac{P}{g}+\frac{V^2}{2 g}+Z=\mathrm{constant}
$$

Using $w=\rho g$ (specific weight), rewrite as:

$$
\frac{P}{w}+\frac{V^2}{2 g}+Z=\mathrm{constant}
$$

Step 3: Bernoulli's Equation for Two Points
For two points 1 and 2 along the streamline:

$$
\frac{P_1}{w}+\frac{V_1^2}{2 g}+Z_1=\frac{P_2}{w}+\frac{V_2^2}{2 g}+Z_2
$$

Where:
- $\frac{P_1}{w}, \frac{P_2}{w}$ : Pressure head at points 1 and 2
- $\frac{V_1^2}{2 g}, \frac{V_2^2}{2 g}$ : Velocity head at points 1 and 2
- $Z_1, Z_2$ : Elevation head at points 1 and 2

Bernoulli's Equation for an Ideal Fluid
For steady, incompressible, and non-viscous fluid flow:

$$
\frac{P}{w}+\frac{V^2}{2 g}+Z=\text { constant }
$$

This expresses the conservation of energy for a fluid in streamline motion.

Assumptions:

• The flow is steady and continuous
• The liquid is ideal and incompressible if the velocity is uniform
• The velocity is uniform in the entire cross-sectional area and is equal to the mean velocity
• The pressure and gravity forces are only considered, others are neglected.
• All frictional losses are neglected
• The flow is irrational
• The ideal, incompressible liquid through a non-uniform pipe.

Limitations:

• Velocity of flow across the cross sectional area of the pipe is assumed to be constant, but it is not possible in actual practice.
• The equation has been derived under the assumption that no external force except gravity and pressure forces are acting on the liquid. However, in reality, a force such as pipe friction acts on the liquid.
• No energy loss is assumed, but kinetic energy is transformed into thermal energy during turbulent flow.

Bernoulli’s equation for real fluid

Real fluid has viscosity, so there are some losses due to frictional force. These losses should be taken into consideration while writing Bernoulli's equation for real fluid.

$\frac{P_1}{w}+\frac{V_1^2}{2 g}+Z_1=\frac{P_2}{w}+\frac{V_2^2}{2 g}+Z_2+h_L$

Where, hL-loss of energy due to friction at inlet and outlet or between two sections considered.

Recommended Topic Video

Solved Examples Based on Bernoulli's Theorem

Example 1: When an air bubble of radius $r$ rises from the bottom to the surface of a lake, its radius becomes $\frac{5 r}{4}$. Taking the atmospheric pressure to be equal to the pressure of a 10 m height of the water column, calculate the approximate depth (in meters) of the lake. Assume the temperature remains constant, and ignore surface tension.

1) 11.2

2) 8.7

3) 9.5

4) 10.5

Solution

- At the bottom surface:

$$
P_1=P_a+\rho g h
$$

Where:
- $P_a$ : Atmospheric pressure
- $\rho$ : Density of the fluid
- $g$ : Acceleration due to gravity
- $h$ : Height of the fluid column
- At the upper surface:

$$
P_2=P_a
$$

Using the continuity equation $P_1 V_1=P_2 V_2$ :

$$
P_1 \cdot \frac{4}{3} \pi r^3=P_2 \cdot \frac{4}{3} \pi \cdot 12564 \cdot r^3
$$

Simplify:

$$
P_1=12564 \cdot P_2
$$

Thus,

$$
\frac{P_1}{P_2}=12564
$$

Substituting the Pressures:
Substitute $P_1=P_a+\rho g h$ and $P_2=P_a$ :

$$
\frac{P_a+\rho g h}{P_a}=12564
$$

$$
1+\frac{\rho g h}{P_a}=12564
$$

Rearranging:

$$
\frac{\rho g h}{P_a}=12564-1=6164
$$

Solve for $h$ :

$$
\rho g h=6164 \cdot P_a
$$

Assume $P_a=10 \mathrm{~N} / \mathrm{m}^2$ :

$$
\begin{aligned}
& \rho g \cdot h=6164 \cdot 10 \\
& h=\frac{6164}{\rho g}=9.5 \mathrm{~m}
\end{aligned}
$$

Hence, the answer is the option (3).

Example 2: Water from a tap emerges vertically downwards with an initial speed of $1.0 \mathrm{~m} / \mathrm{s}$. The cross-sectional area of the tap is $10^{-4} \mathrm{~m}^2$. Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. Find the cross-sectional area $\left(A_2\right)$ of the stream at 0.15 m below the tap, expressed as $x \times 10^{-5} \mathrm{~m}^2$. What is the value of $x$ ?
(Take $g=10 \mathrm{~m} / \mathrm{s}^2$ ).

1) 2

2) 5

3) 0.5

4) 0.2

Solution:

Using Bernoulli's theorem we get

$$
V_2^2-V_1^2=2 g h
$$

Rearranging to solve for $V_2$ :

$$
V_2=\sqrt{V_1^2+2 g h}
$$

Substituting the values:

$$
\begin{gathered}
h=0.15 \mathrm{~m}, V_1=1 \mathrm{~m} / \mathrm{s}, g=9.8 \mathrm{~m} / \mathrm{s}^2 \\
V_2=\sqrt{1^2+2(9.8)(0.15)} \\
V_2=\sqrt{1+2.94}=\sqrt{3.94} \approx 2 \mathrm{~m} / \mathrm{s}
\end{gathered}
$$

$\begin{gathered}\left(10^{-4}\right)(1)=A_2(2) \\ A_2=\frac{10^{-4}}{2}=0.5 \times 10^{-4}=5 \times 10^{-5} \mathrm{~m}^2\end{gathered}$

Hence, the answer is the option (2).

Example 3: Bernoulli's principle is based on

1) Conservation of momentum

2) Conservation of mass

3) Conservation of energy

4) Both (1) and (3)

Solution:

Bernoulli's Principle

The total energy (Pressure energy, Potential energy, and Kinetic energy ) per unit volume or mass of an incompressible and nonviscous fluid in steady flow through a pipe remains constant.

wherein

The proper expression for Bernoulli's equation is:

$$
P+\rho g h+\frac{1}{2} \rho v^2=\mathrm{constant}
$$

Where:
- $P$ : Pressure energy
- $\rho g h$ : Potential energy per unit volume
- $\frac{1}{2} \rho v^2$ : Kinetic energy per unit volume

So each term represents energy. So it is the conservation of energy.

Hence, the answer is the option (3).

Example 4: According to Bernoulli's equation

$$
\frac{P}{\rho g}+h+\frac{v^2}{2 g}=\text { constant }
$$ant A+B+C

The terms A, B, and C are generally called

1) Gravitational head, pressure head and Velocity head

2) Gravity, gravitational head and velocity head.

3) Pressure head, gravitational head and Velocity head.

4) Gravity, pressure head and velocity head

Solution:

Bernoulli's theorem for unit mass

$$
\frac{P}{\rho g}+h+\frac{v^2}{2 g}=\text { constant }
$$

Where:
- $\frac{P}{\rho g}$ : Pressure head
- $\frac{v^2}{2 g}$ : Velocity head
- $h$ : Gravitational head (elevation head)

Hence, the answer is the option (3).

Example 5: Water enters a house through a pipe with an inlet diameter of 2.0 cm at an absolute pressure of 4.0 × 10⁵ Pa (about 4 atm). A 1.0 cm diameter pipe leads to the second-floor bathroom 5.0 m above. When the flow speed at the inlet pipe is 1.5 m/s, what will be the flow speed, pressure and volume flow rate in the bathroom respectively?

1. $6 \mathrm{~m} / \mathrm{s}, 6.6 \times 10^5 \mathrm{~Pa}, 4.7 \times 10^{-4} \mathrm{~m}^3 / \mathrm{s}$
2. $3 \mathrm{~m} / \mathrm{s}, 3.3 \times 10^5 \mathrm{~Pa}, 5.7 \times 10^{-4} \mathrm{~m}^3 / \mathrm{s}$
3. $4 \mathrm{~m} / \mathrm{s}, 4 \times 10^5 \mathrm{~Pa}, 3.2 \times 10^{-4} \mathrm{~m}^3 / \mathrm{s}$
4. $6 \mathrm{~m} / \mathrm{s}, 3.3 \times 10^5 \mathrm{~Pa}, 4.7 \times 10^{-4} \mathrm{~m}^3 / \mathrm{s}$

Solution:

Let points 1 and 2 be at the inlet pipe and at the bathroom, then from the continuity equation,

Step 1: Continuity Equation
From the continuity equation:

$$
A_1 v_1=A_2 v_2
$$

Solving for $v_2$ :

$$
v_2=6.0 \mathrm{~m} / \mathrm{s}
$$

Step 2: Bernoulli's Equation
Applying Bernoulli's equation between the inlet ( $y_1=0$ ) and the bathroom ( $y_2=5.0 \mathrm{~m}$ ):

$$
P_2=P_1-\frac{1}{2} \rho\left(v_2^2-v_1^2\right)-\rho g\left(y_2-y_1\right)
$$

Substitute the given values to find $P_2$ :

$$
P_2=3.3 \times 10^5 \mathrm{~Pa}
$$

The volume flow rate $(Q)$ is given by:

$$
Q=A_2 v_2=A_1 v_1
$$

Substitute $A_2=\frac{\pi}{4}(0.01)^2$ and $v_2=6.0 \mathrm{~m} / \mathrm{s}$ :

$$
\begin{gathered}
Q=\frac{\pi}{4}(0.01)^2 \cdot 6 \\
Q=4.7 \times 10^{-4} \mathrm{~m}^3 / \mathrm{s}
\end{gathered}
$$

Hence, the answer is the option (4).