Boltzmann Constant - Definition, Formula, Value, FAQs
The Boltzmann constant is a proportionality constant that is associated with the relative average kinetic energy of the particles present inside the gas with the gas’s thermodynamic temperature. It happens in the description of the gas constant and in Planck's ordinance of black-body radiation and formula of Boltzmann entropy and in the kelvin scale. It was the Austrian researcher Ludwig Boltzmann, who came up with this constant formula, and thus was given the name Boltzmann constant, consisting of dimensions similar to the entropy that is energy divided by the temperature.
JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide
JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days
NEET 2025: Syllabus | High Scoring Topics | PYQs
The Boltzmann constant is one of the most well received seven defining constants which has applications in different mergers to describe the SI base units of the seven defining constants.
NCERT Physics Notes :
History of the invention of the Boltzmann constant
The name Boltzmann constant is given the name after the Austrian researcher, Ludwig Boltzmann in the 19th century. Even though it was Ludwig first in the year 1877, who associated probability and entropy, in the black body radiation derivation initially in 19th century, however the association was not at all once indicated with a particular constant until Planck, invented the k and presented the most accurate value for it in the ordinance of the black body radiation derivation in the 19th century initially. Prior to the 19th century, calculations regarding the factors of Boltzmann were not put in writing applying the molecule per energy and the Boltzmann constant, instead applying a gas constant form, R and energy in macroscopy and quantities in macroscopy of the compound.
In the year 2017, the most precise calculations of the Boltzmann constant were acquired by gas thermometry which is acoustic, which represent the velocity of the volume of the monatomic gas in a chamber which is triaxial ellipsoid with applying resonances of acoustic and microwave. This time- consuming exertion was accepted with various experiments by many laboratories. It is one of the most well received cornerstones of the year 2019 SI base unit redefinition. Based upon the calculations, the CODATA endorsed 1.380 649 × 10-23 J.K-1 to be the concluding Boltzmann constant value to be applied for the international system of the units.
Also read -
- NCERT Solutions for Class 11 Physics
- NCERT Solutions for Class 12 Physics
- NCERT Solutions for All Subjects
Formula of Boltzmann constant/ Write kb formula.
On account of equation of ideal gas
PV=nRT
Where P stands for the pressure in the units of pascals
V stands for the volume in the units of meter cube
N stands for the number of moles of the gas present or given
R stands for the proportionality constant or the gas constant
T stands for the temperature in the unit of kelvin.
R=N/NA
Where NA represents Avogadro’s number and N is the number of molecules present
Numerical value of Avogadro’s number is 6.022×1023 per mole molecules
The numerical value of R is 8.314 Joule/mole K.
Since the pressure, number of moles present and the volume are all quantities in macroscopy, but now we are considering the gas molecules which would be represented only in microscopic quantities.
Also read :
- NCERT solutions for Class 11 Physics Chapter 13 Kinetic Theory
- NCERT Solutions for Class 11th Physics Chapter 13 Kinetic Theory
- NCERT notes Class 11 Physics Chapter 13 Kinetic Theory
After rearranging the equation, we get
PV=N× K b× T
Where again P stands for pressure in the unit of pascals
V stands for the volume in the unit of meter cubes
N stands for the number of moles of gas present or given in consideration
And T stands for the temperature.
Since the values N×K b and n× R are equivalent
Equating both the sides of the equation we get
n× R= N× K b
K b = n/ N×R
Formula of Boltzmann constant: K b = 1 / Na ×R
Above equation gives the relationship between boltzmann constant and R.
Upon calculation of the above equation written, we get Boltzmann constant value
Kb = 1.3806452 × 10-23 Joule per kelvin
Related Topics Link, |
SI units of Boltzmann constant is joule per kelvin
The equation written above concludes that the energy of the molecules of the gas is directly proportional to the absolute temperature.
Boltzmann constant in e V
Boltzmann constant is applied to represent the factor of Boltzmann, the idea of entropy in description of the idea of this constant as we are discussing the stochastic of the gas molecules upon the gas which is warmed.
Boltzmann constant in electron volt/boltzmann constant in ev
is equivalent to 0.000086173324 electron volts per kelvin.
The Boltzmann constant value in erg per kelvin
The Boltzmann constant value in K b in cgs units is given by 1.3806542×10-16 erg per kelvin
Boltzmann constant applications
numerical methodology of both the quantum and classical branches of physics.
Boltzmann constant is interconnected link between microscopic and macroscopic branches of physics
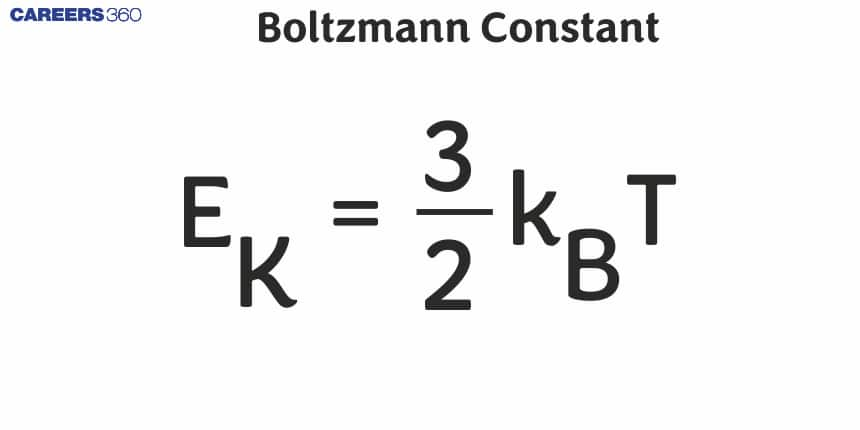
For a classical system of temperature of equilibrium denoted by E, the average energy per degree of freedom is k ×E/ 2
The total thermal energy of the gas molecules present is given by 3× D ×E/2 = m×z2/2
Where z2 stands for the average of the squared speed of the molecules of the gas present, and E stands for the absolute temperature in the unit of kelvin.
Thermodynamics of Clausius
Boltzmann proved that the numerical quantity is equivalent to the 2/3rd of the Clausius entropy of thermodynamics of a molecule of ideal gas.
Boltzmann called the gamma as the permutability measure.
Constant of Planck.
Dividing the constant of Planck p by the 4.8 ×10-34
K b = p/ 4.8×10-11 = 6.62610-11
We get the K b value as 1.38041×10-23
We came to know that the irregularities of the entropy or the particles which directly interconnected to the molecule temperature inside the gas, which means higher the temperature the more will be the entropy.
Also check-
Frequently Asked Questions (FAQs)
K is applied as a coulomb constant in physics which is numerically equivalent to the value of K = 9×109 newton meter square and centimeter square.
The constant is a physical quantity that is known to be ubiquitous in nature and has a constant numerical value in all the conditions applied.
Boltzmann constant is the constant of the ratio of gas to Avogadro’s number equivalent to the numerical value of 1.381×10-23 joules per kelvin as in the case of where the molecules in existence are equivalent to Avogadro’s number. Boltzmann constant has significance in many branches namely, Planck’s constant, Clausius thermodynamics and is also an interconnected link between microscopic and macroscopic branches of physics.
S= kb log w is the equation for Boltzmann entropy.
In semiconductors, the Shockley diode equation determines the interconnection between the flow rate of electric current and the potential of electrostatic along p and n junction diodes which depends on a particular voltage called the thermal voltage, which is abbreviated as VT. the thermal voltage totally depends on absolute temperature T as
VT = kT/ q where q stands for the magnitude of the electron’s electric charge.
Boltzmann constant k is equal to 228.5991672dB (W/K/Hz)
Boltzmann constant can be expressed in units such as, J/K, eV/K, cal/K, dB, erg/K etc.
Also Read
18 Nov'24 04:58 PM
12 Nov'24 10:12 PM
12 Nov'24 09:45 PM
12 Nov'24 09:42 PM
12 Nov'24 01:31 AM
25 Sep'24 03:48 PM
25 Sep'24 11:43 AM
24 Sep'24 11:02 PM