Bulk Modulus of Elasticity Definition Formula with Example

One of the amazing concepts we examine in the strength of the material topic is the bulk modulus. Recalling the keywords associated with bulk modulus will help us comprehend what it is and how it is defined. As we examine Hooke's law, we find that stress and strain in the material are exactly proportionate. The modulus of elasticity is the proportionality constant that resulted from Hooke's law.

Hooke's Law Definition

It is the basic law of elasticity. It states that the extension produced in a wire is directly proportional to the load attached to it.

Thus, according to Hooke's law, extension $\propto$ load
However, this proportionality holds good up to a certain limit, called the elastic limit.

According to the Hooke's law,
or stress $\propto$ strain
or $\quad$ stress $=$ constant $\times$ strain
or $\quad \frac{\text { stress }}{\text { strain }}=$ constant
This constant of proportionality is called the modulus of elasticity or the coefficient of elasticity of the material. Its value depends upon the nature of the material of the body and the manner in which the body is deformed. There are three moduli of elasticity namely Young's modulus $(\mathrm{Y})$, bulk modulus $(\mathrm{K})$ and modulus of rigidity $(\eta)$ corresponding to the three types of the strain.

What is Stress

Stress is defined as the restoring force per unit area set up in the body when deformed by the external force. Thus,

$
\text { stress }=\frac{\text { restoring force }}{\text { area }}
$

What is Strain

When a deforming force acts on a body, it undergoes a change in its dimensions and the body is said to be deformed or strained.

The ratio of change in the dimension of the body to its original dimension is called strain.

Since a body can have three types of deformations i.e. in length, volume or shape, likewise there are the following three types of strains:

(i) Longitudinal Strain

It is defined as the increase in length per unit of original length when deformed by external force. It is also called linear strain or tensile strain.

Thus, longitudinal strain $=\frac{\text { change in length }}{\text { original length }}=\frac{l}{\mathrm{~L}}$, where L is the original length and $l$, the increase in length.

(ii) Volumetric Strain

It is defined as the change in volume per unit of original volume when deformed by the external force.

Thus, volumetric strain $=\frac{\text { change in volume }}{\text { original volume }}=\frac{\Delta \mathrm{V}}{\mathrm{V}}$,
where V is the original volume and $\Delta \mathrm{V}$, the change in volume.

(iii) Shear Strain

When change takes place in the shape of the body, the strain is called the shear strain.

It is defined as the angle $\theta$ (in radian), through which a line originally perpendicular to the fixed face gets turned on applying tangential deforming force.

What is Bulk Modulus?

Bulk Modulus is defined as the ratio of the normal stress to the volumetric strain. It is denoted by K.

Thus, in accordance with Hooke's law, we have

$
\mathrm{K}=\frac{\text { normal stress }}{\text { volumetric strain }}
$

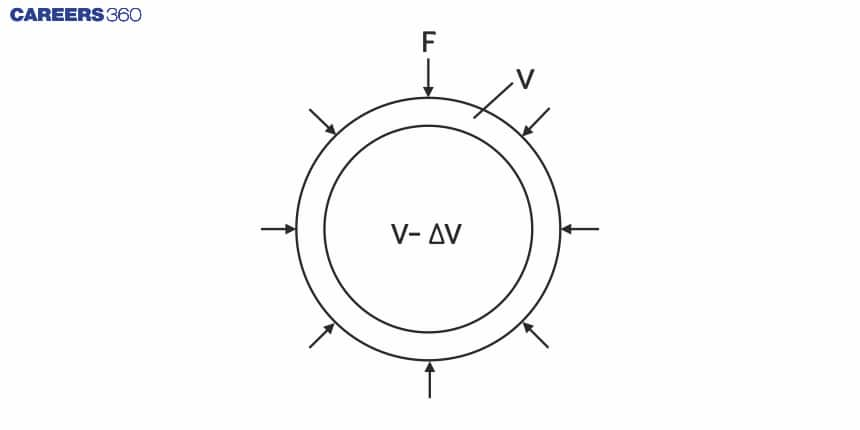
Consider a sphere of volume V and surface area $a$ [Fig.] Suppose that a force F which acts uniformly over the whole surface of the sphere decreases its volume by $\Delta \mathrm{V}$. Then,

$
\text { normal stress }=\frac{\mathrm{F}}{a}
$

and volumetric strain $=-\frac{\Delta \mathrm{V}}{\mathrm{V}}$
The negative sign indicates that on increasing the stress, the volume of the sphere decreases. Therefore,
or

$
\begin{aligned}
& K=\frac{F / a}{-\Delta V / V} \\
& K=-\frac{F V}{a \Delta V}
\end{aligned}
$
Now, $\frac{\mathrm{F}}{a}=p$, the pressure applied over the sphere.
Therefore, $\quad \mathrm{K}=-\frac{p \mathrm{~V}}{\Delta \mathrm{V}}$
The units of bulk modulus are Pa or $\mathbf{N ~ m}^{-2}$ in SI.

Also, check

NCERT Exemplar Class 11th Physics Solutions

NCERT Exemplar Class 12th Physics Solutions

NCERT Exemplar Solutions for All Subjects

Factors Affecting Bulk Modulus

We will discuss some important factors

• Material composition: Particle arrangement affects a material's bulk modulus. Metals, for instance, have a larger bulk modulus than gases and liquids.
• Temperature: A material's bulk modulus decreases with increasing temperature due to greater molecular vibration, which makes the material easier to compress.
• Pressure: As a material's pressure rises, its molecules are forced closer together, raising the material's bulk modulus and making it more difficult to compress.
• Crystalline structure: A material's bulk modulus may be impacted by its crystalline structure. For example, the rigid crystalline lattice of a diamond contributes to its high bulk modulus.

Compressibility

Compressibility. The reciprocal of the bulk modulus of a material is called its compressibility. Therefore,

$
\text { compressibility }=\frac{1}{\mathrm{~K}}
$
The units of compressibility are reciprocal of those of the bulk modulus i.e. the units of compressibility are $\mathrm{Pa}^{-1}$ or $\mathrm{N}^{-1} \mathrm{~m}^2$ in SI.

Bulk Modulus of Some Common Materials (Solids and Liquid)

Generally, the bulk modulus is used for liquids rather than solids. Because bulk modulus resembles incompressibility, and we know the liquids are incompressible.