Centre Of Mass Of Semicircular Ring

The concept of the centre of mass is pivotal in understanding the distribution of mass in physical systems. For a semicircular ring, a classic problem in mechanics, determining this point helps in analyzing its behaviour under various forces and torques. In real life, this principle is not just an academic exercise but has practical implications. For instance, when designing wheel rims for bicycles or vehicles, engineers must account for the centre of mass to ensure stability and balance. Similarly, in architectural structures that incorporate curved elements, knowing the centre of mass helps in achieving equilibrium and preventing potential structural failures. By exploring the centre of mass of a semicircular ring, we gain insights into both theoretical and practical aspects of mass distribution, enhancing our understanding of equilibrium in real-world applications.

Definition of Centre of Mass

The Centre of mass of a body is defined as a single point at which the whole mass of the body or system is imagined to be concentrated and all external forces are applied there. It is the point where if a force is applied it moves in the direction of the force without rotating.

Centre of Mass of a Continuous Distribution

The centre of mass of a continuous distribution is a key concept in physics that extends beyond simple, discrete systems to more complex, continuous ones. Unlike objects with distinct masses located at specific points, continuous distributions involve mass spread over a region, such as a rod, a plate, or even a fluid. To find the centre of mass in such cases, we consider each infinitesimally small mass element and calculate its contribution to the overall position.

$x_{c m}=\frac{\int x d m}{\int d m}, y_{c m}=\frac{\int y d m}{\int d m}, z_{c m}=\frac{\int z d m}{\int d m}$

Where dm is the mass of the small element. x, y, z are the coordinates of the dm part.

The Centre of Mass of the Semicircular Ring

The centre of mass of a semicircular ring, a fundamental concept in physics, represents the average position of its mass distribution. This point is crucial for analyzing the ring's mechanical behaviour, particularly in understanding how it balances and responds to forces. For a semicircular ring, the centre of mass is located along the central axis of symmetry, positioned at a specific distance from the flat edge, which can be calculated using integral calculus

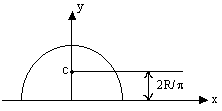
Have a look at the figure of the semicircular ring.

Since it is symmetrical about the y-axis on both sides of the origin

So we can say that its $x_{c m}=0$

And it's $z_{c m}=0$ as the z-coordinate is zero for all particles of the semicircular ring.

Now, we will calculate its $y_{\mathrm{cm}}$ which is given by

$y_{c m}=\frac{\int y \cdot d m}{\int d m}$

So, Take a small elemental arc of mass dm at an angle $\theta$ from the x-direction.

Its angular width $\mathrm{d} \theta$

If the radius of the ring is R then its y coordinate will be Rsin$\theta$

So, $d m=\frac{M}{\pi R} * R d \theta=\frac{M}{\pi} d \theta$
$y_{\mathrm{As},} y_{\mathrm{cm}}=\frac{\int y \cdot d m}{\int d m}$
$y_{c m}=\frac{\int_0^\pi \frac{M}{\pi R} \times R \times R \sin \theta d \theta}{M}=\frac{R}{\pi} \int_0^\pi \sin \theta d \theta=\frac{2 R}{\pi}$

Recommended Topic Video

Solved Examples Based on the Centre of Mass of the Semicircular Ring

Example 1: What is the position of the centre of mass of a semicircular ring shown below -

$\begin{aligned} & \text { 1) }\left(0, \frac{2 R}{3 \pi}\right) \\ & \text { 2) }\left(\frac{2 R}{3 \pi}, 0\right) \\ & \text { 3) }\left(\frac{2 R}{\pi}, 0\right) \\ & \text { 4) }\left(0, \frac{2 R}{\pi}\right)\end{aligned}$

Solution

Position of centre of mass for semicircular ring -

Have a look at the figure of the semicircular ring.

Since it is symmetrical about the y-axis on both sides of the origin

So we can say that its $x_{\mathrm{cm}}=0$

And it's $z_{\mathrm{cm}}=0$ as the z-coordinate is zero for all particles of the semicircular ring.

Now, we will calculate its which is given by

$y_{c m}=\frac{\int y \cdot d m}{\int d m}$

So, Take a small elemental arc of mass dm at an angle $\theta$ from the x-direction.

Its angular width d

If the radius of the ring is R then its y coordinate will be $R \sin \theta$
So, $d m=\frac{M}{\pi R} * R d \theta=\frac{M}{\pi} d \theta$
$y_{\mathrm{cm}}=\frac{\int y \cdot d m}{\int d m}$
So, $y_{c m}=\frac{\int_0^\pi \frac{M}{\pi R} \times R \times R \sin \theta d \theta}{M}=\frac{R}{\pi} \int_0^\pi \sin \theta d \theta=\frac{2 R}{\pi}$
Now, the co-ordinate of the centre of mass is $\left(0, \frac{2 R}{\pi}\right)$

Hence, the answer is the option (4).

Example 2: What is the position of the centre of mass of a semicircular ring whose base is placed on $x-a x i s$ and peak point on the $y-a x i s$. Also, the centre of the ring is at $(2,0,0)$

1) $(2,0,0)$
2) $\left(2, \frac{2 R}{\pi}, 0\right)$
3) $\left(2,0, \frac{2 R}{\pi}\right)$
4) $\left(\frac{2 R}{\pi}, \frac{2 R}{\pi}, \frac{2 R}{\pi}\right)$

Solution

The centre of the ring is at $(2,0,0)$
So, $x_{c m}=2$
And $y_{c m}=\frac{2 R}{\pi}$
And $z_{c m}=0$
So coordinates of $C O M$ will be $\left(2, \frac{2 R}{\pi}, 0\right)$

Hence, the answer is the option (2).

Example 3: The position of the centre of mass of a uniform semi-circular wire of radius placed in X-Y plane with its centre at the origin and the line joining its ends as $x$-axis is given by $\left(0, \frac{x R}{\pi}\right)$.

Then, the value of $|x|$ is__________.

1) 2

2) 3

3) 4

4) 5

Solution

$\begin{aligned} & y_{c m}=\frac{2 R}{\pi} \\ & x_{c m}=0 \\ & \therefore x=2\end{aligned}$

Hence, the answer is the option (1).

Example 4: A train of mass M is moving on a circular track of radius ' R ' with constant speed V. The length of the train is half of the perimeter of the track. The linear momentum of the train will be

1) 0
2) $\frac{2 M V}{\pi}$
3) $M V R$
4) $M V$

Solution

Centre of Mass of semicircular ring

It lies at a distance of $\frac{2 R}{\pi}$ from the centre of the ring along its axis.

If we treat the train as a ring of mass 'M' then its COM will be at a distance $\frac{2 R}{\pi}$ from the centre of the circle. The velocity of centre of mass is :
$
\begin{aligned}
& V_{C M}=R_{C M} \cdot \omega=\frac{2 R}{\pi} \cdot \omega=\frac{2 R}{\pi}\left(\frac{V}{R}\right) \quad\left(\because \omega=\frac{V}{R}\right) \\
& \Rightarrow V_{C M}=\frac{2 V}{\pi} \Rightarrow M V_{C M}=\frac{2 M V}{\pi}
\end{aligned}
$
As the linear momentum of any system $=\mathrm{MV}_{\mathrm{CM}}$
$\therefore$ The linear momentum of the train $=\frac{2 M V}{\pi}$

Hence, the answer is the option (2).

Summary

The centre of mass of a semicircular ring is a crucial concept in physics, representing the average position of its mass distribution. Located along the central axis of symmetry, it helps in analysing the ring’s behaviour under forces and torques. By calculating the centre of mass using integral calculus, engineers and architects can apply this knowledge to design stable and balanced structures, such as bicycle wheels and curved architectural elements. The practical applications extend to solving various problems involving mass distribution, stability, and equilibrium in real-life scenarios.