Electric Dipole - Definition, Formula, FAQs

Two charges, equal in magnitude, but opposite in sign separated by a small distance form a dipole. It is an elementary magnet whose positive end attracts negative ends while repelling positive ones; similarly, each side acts like a beginning and an end. Electric dipoles are essential for investigating how molecules interact since most of these compounds have such properties due to differences in their electron distribution between nuclei making them have a partial positive charge on one side while having partial negative charges on other angles of inclination towards this aspect instead if looked at it from different perspectives at the same time it makes it appear both as positive and negative but since they are near each other from the point at which we stand there is no way they could be seen. A torque is exerted on the dipole by the electric field; this torque tends to align the dipole with the field.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Define Electric Dipole
2. What is electric Dipole Moment?
3. Solved Examples Based on Electric Dipole

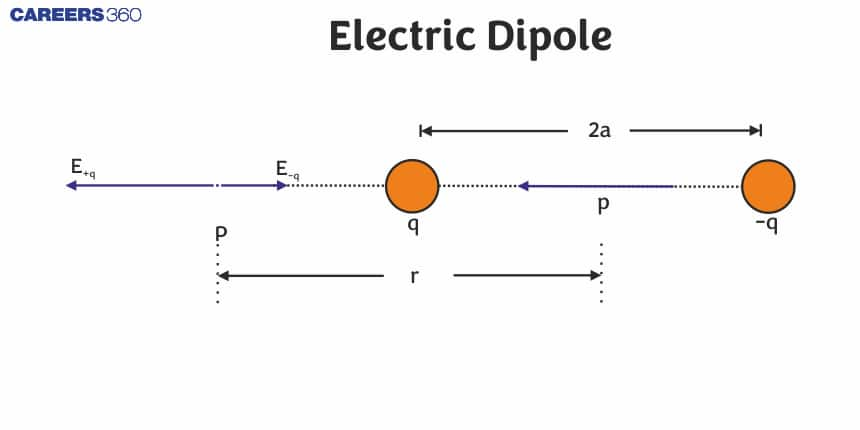
Define Electric Dipole

An electric dipole is a system of two equal and opposite point charges separated by a very small and finite distance.

Below is the figure showing an electric dipole consisting of two equal and opposite point charges $-q$ and $+q$ separated by a small distance $2 l$.

What is electric Dipole Moment?

The strength of an electric dipole is measured by a vector quantity known as the electric dipole moment. Its magnitude is equal to the product of the magnitude of either charge and the distance between the two charges,

i.e. for the dipole, as shown in the above figure dipole moment is given as

$$
(\vec{P})=q(\overrightarrow{2 l})
$$
And its direction is along the line from -q to +q.
The $\mathrm{S} . \mathrm{I}$ unit is $\mathrm{C}-\mathrm{m}$ and its CGS unit is Debye ( 1 Debye $=3.3 \times 10^{-30} \mathrm{C}-m$ )

Related Topics

• Electric Charge
• Epsilon Naught Value
• Value of Electron
• Electric Field Lines
• Electrostatics

Potential Due to an Electric Dipole

Consider an electric dipole, with charges $+q$ and $-q$ separated by distance $d$, having equal magnitude and O being the midpoint between the two charges. Now, the electric potential at any point $C$, such that $O C=r$, due to the electric dipole will be given as:

$$
V=\frac{p \times \cos \theta}{4 \pi e r^2}
$$
Case 1: When $\theta=90^{\circ}$, Electric potential,

$$
\mathrm{V}=0
$$
Case 2: When $\theta=0^{\circ}$, Electric potential,

$$
V=\frac{p}{4 \pi e r^2}
$$

Also, read

• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects

Electric Field Due to an Electric Dipole

Coulomb's law and the superposition principle can be used to calculate the electric field of a pair of charges ( -q and q ) at any point in space. The results are particularly simple and clear for the following two scenarios.
The electric field is due to a dipole at any point (the line connecting the two charges).

$$
E=\frac{2 p}{4 \pi e_0 r^3}
$$

Electric field due to dipole at equatorial point (a plane perpendicular to the dipole axis through its center).

$$
E=\frac{-p}{4 \pi e_0 r^3}
$$

Direction of Electric Dipole Moment

The electric dipole moment is a vector quantity. It has a defined direction which is from the negative charge to the positive charge. However, it is important to remember that this convention of direction is only followed in Physics.

Physical Significance of Dipole

A dipole has physical significance in the unique electric field generation, interaction with external fields, and contribution to polarization in materials. Chemically, it is behind molecular interactions; in physics, it describes dielectric properties; and is the basis for antenna technology emitting electromagnetic waves.

Solved Examples Based on Electric Dipole

Example 1: An electric dipole is placed in an electric field generated by a point charge

1) The net electric force on the dipole must be zero

2) The net electric force on the dipole may be zero

3) The torque on the dipole due to the field must be zero

4) The torque on the dipole due to the field may be zero

Solution:

Electric dipole

Two equal and opposite charges are separated by a small distance.

wherein

Point charge produces a non-uniform electric field

Example 2: A point dipole $\vec{p}=-p_0 \hat{x}_{\text {is kept at the origin. The potential }}$ and electric field due to this dipole on the $y$-axis at a distance $d$ are, respectively : ( Take V=0 at infinity)
1) $0, \frac{-\vec{p}}{4 \pi \epsilon_0 d^3}$
2) $0, \frac{\vec{p}}{4 \pi \epsilon_0 d^3}$
3) $\frac{|\vec{p}|}{4 \pi \epsilon_0 d^2}, \frac{-\vec{p}}{4 \pi \epsilon_0 d^3}$
4) $\frac{|\vec{p}|}{4 \pi \epsilon_0 d^2}, \frac{\vec{p}}{4 \pi \epsilon_0 d^3}$

Solution:

$\begin{aligned} V & =0 \\ E & =\frac{-k \vec{p}}{r^3} \\ \vec{E} & =\frac{-\vec{p}}{4 \pi \epsilon_0 d^3}\end{aligned}$

Example 3: Shown in the figure is a shell made of a conductor. It has an inner radius a and outer radius $b$, and carries charge $Q$, At its centre is a dipole $\vec{p}$ as shown. In this case :

1) surface charge density on the outer surface depends on $|\vec{p}|$
2) The electric field outside the shell is the same as that of a point charge at the centre of the shell
3) surface charge density on the inner surface is uniform and equal to

$
\frac{(Q / 2)}{4 \pi a^2}
$

4) surface charge density on the inner surface of the shell is zero everywhere

Solution:

The charge distribution at equilibrium on the conductor will be like :

The net charge on the outer surface $=Q$
The total charge on the inner surface $=0$
If we take a Gaussian surface outside the shell.
So net charge inside the Gaussian surface will be Q .
So far any observed outside the shell, the resultant electric field is due to $Q$ uniformly distributed on the outer surface and it is equal to

$
E=\frac{K Q}{r^2}
$
So electric field outside the shell is the same as that of a point charge at the centre of the shell.

Example 4: Two charges $+3.2 * 10^{-19}$ and $-3.2 * 10^{-19} \mathrm{C}$ placed at 2.4 A apart from an electric dipole. It is placed in a uniform electric field of intensity $4 * 10^5 \mathrm{volt} / \mathrm{m}$. The electric dipole moment is
1) $15.36 * 10^{-29}$ coulomb $\times m$
2) $15.36 * 10^{-19}$ coulomb $\times \mathrm{m}$
3) $7.68 * 10^{-29}$ coulomb $\times m$
4) $7.68 * 10^{-19}$ coulomb $\times m$

Solution:

Dipole moment
$
(\vec{P})=q(\overrightarrow{2 l})
$
Its S.I unit is C-m
and its CGS unit is Debye ( ${ }^1$ Debye $=3.3 \times 10^{-30} \mathrm{C}-\mathrm{m}$ )
Dipole moment $p=q(2 I)$

$
=3.2 \times 10^{-19} \times\left(2.4 \times 10^{-10}\right)=7.68 \times 10^{-29} \mathrm{Cm}
$

Hence, the answer is the option (3).

Example 5: Two opposite and equal charges $4 \times 10^{-8}$ when placed $2 \times 10^{-2}$ away, form a dipole. If this dipole is placed in an external electric field $4 \times 10^{-8}$, the value of maximum torque and the work done in rotating it through $180^{\circ}$ will be
1) $64 \times 10^{-4} \mathrm{Nm}$.. and.. $64 \times 10^{-4} \mathrm{~J}$
2) $32 \times 10^{-4} \mathrm{Nm}$.. and.. $32 \times 10^{-4} J$
3) $64 \times 10^{-4} \mathrm{Nm} .$. and.. $32 \times 10^{-4} J$
4) $32 \times 10^{-4} \mathrm{Nm}$.. and.. $64 \times 10^{-4} J$

Solution:

Given Data:
- Charge, $q=4 \times 10^{-8} \mathrm{C}$
- Separation between charges, $d=2 \times 10^{-2} \mathrm{~m}$
- Electric field, $E=4 \times 10^{-8} \mathrm{~N} / \mathrm{C}$

Step 1: Calculate the Dipole Moment ( $p$ )
The dipole moment $p$ is given by:

$$
p=q \times d
$$
Substitute the values:

$$
p=\left(4 \times 10^{-8}\right) \times\left(2 \times 10^{-2}\right)=8 \times 10^{-10} \mathrm{Cm}
$$
Step 2: Calculate the Maximum Torque ( $\tau$ )
The torque experienced by a dipole in a uniform electric field is given by:

$$
\tau=p \cdot E \cdot \sin \theta
$$

For maximum torque, $\theta=90^{\circ}$, so $\sin \theta=1$.

$$
\tau_{\max }=p \cdot E
$$
Substitute the values:

$$
\tau_{\max }=\left(8 \times 10^{-10}\right) \times\left(4 \times 10^{-8}\right)=32 \times 10^{-18} \mathrm{Nm}
$$
To match the options, convert this to scientific notation:

$$
\tau_{\max }=32 \times 10^{-4} \mathrm{Nm}
$$
Step 3: Calculate the Work Done in Rotating the Dipole through $180^{\circ}$
The work done to rotate a dipole through an angle $\theta$ in a uniform electric field is given by:

$$
W=p \cdot E \cdot(1-\cos \theta)
$$
For $\theta=180^{\circ}, \cos \theta=-1$ :

$$
W=p \cdot E \cdot(1-(-1))=2 \cdot p \cdot E
$$

Substitute the values:

$$
W=2 \times\left(8 \times 10^{-10}\right) \times\left(4 \times 10^{-8}\right)=64 \times 10^{-18} \mathrm{~J}
$$
To match the options, convert this to scientific notation:

$$
W=64 \times 10^{-4} \mathrm{~J}
$$

Hence, the answer is the option (4).