Electric Field Due To An Infinitely Long Charged Wire

Imagine standing near a tall, endless fence made of electrified metal. The electric field created by this fence would stretch out in all directions, influencing anything with a charge nearby. In physics, we often model such scenarios with an "infinitely long charged wire" to simplify calculations and understand the behaviour of electric fields over large distances.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Electric field due to an infinite line charge
2. Solved Examples Based on Electric Field Due to an Infinite Line Charge
3. Summary

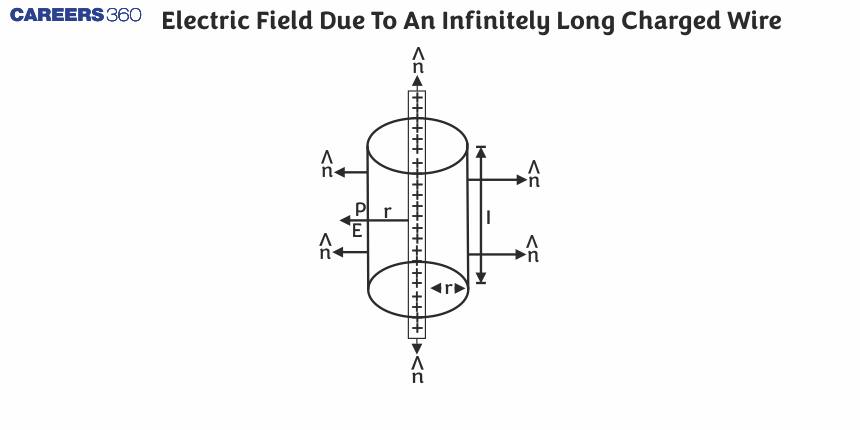
When we consider an infinitely long charged wire, we assume the wire extends infinitely in both directions, with a uniform charge distribution along its length. This setup creates a unique electric field pattern that is symmetrical around the wire. Understanding this electric field is crucial in many applications, from designing electrical circuits to understanding the behaviour of charged particles in various fields. In this article, we'll explore how this electric field is calculated and discuss some practical examples to solidify the concept.

Electric field due to an infinite line charge

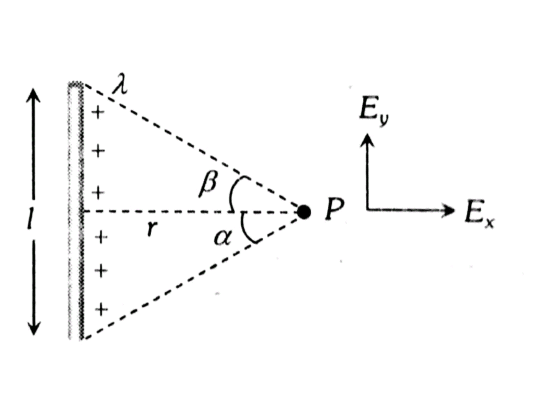
Let us assume that positive electric charge Q is distributed uniformly along a line, lying along the $y$-axis. We have to find the electric field at point $D$ on the $x$ axis at a distance $r_0$ from the origin. Let us divide the line charge into infinitesimal segments, each of which acts as a point charge; let the length of a typical segment at height $l$ be $d l$. If the charge is distributed uniformly with the linear charge density $\lambda$, then the charge $d Q$ in a segment of length $d l$ is $d Q=\lambda d l$, At point D, the differential electric field dE created by this element is:

$
d E=\frac{d Q}{4 \pi \varepsilon_0 r^2}=\frac{\lambda d l}{4 \pi \varepsilon_0 r^2}=\frac{\lambda d l}{4 \pi \varepsilon_0 r_0^2 \sec ^2 \theta}
$

In triangle $A O D ; O A=O D \tan \theta$, i.e., $l=r_0 \tan \theta$
Differentiating this equation with respect to $\theta$, we get
$
d l=r_0 \sec ^2 \theta d \theta
$

Substituting the value of $d l$
$
d E=\frac{\lambda d \theta}{4 \pi \theta_0 r_0}
$

Field $d E$ has components $d E_x d E_y$ given by
$
d E_x=\frac{\lambda \cos \theta d \theta}{4 \pi \varepsilon_0 r_0} \text { and } d E_y=\frac{\lambda \sin \theta d \theta}{4 \pi \varepsilon_0 r_0}
$

If the wire has a finite length and the angles subtended by ends of the wire at a point are $\theta_1$ and $\theta_2$, the limits of integration will be
$
\begin{aligned}
E_x & =\int_{-\theta_1}^{\theta_2} \frac{\lambda \cos \theta d \theta}{4 \pi \varepsilon_0 r_0} \\
& =\frac{\lambda}{4 \pi \varepsilon_0 r_0}\left(\sin \theta_1+\sin \theta_2\right) \\
E_y & =\int_{-\theta_1}^{+\theta_2} \frac{\lambda \sin \theta d \theta}{4 \pi \varepsilon_0 r_0} \\
& =\frac{\lambda}{4 \pi \varepsilon_0 r_0}\left(\cos \theta_1-\cos \theta_2\right)
\end{aligned}
$

Special Case

1.If the line is infinite then the $\theta_1=\theta_2=90^{\circ}$

Putting the value, we get -
$
\begin{aligned}
E_x & =\frac{\lambda}{2 \pi \varepsilon_o r_o} \\
E_y & =0
\end{aligned}
$

2.If the line is semi-infinite then the $\theta_1=0$, and $\theta_2=90^{\circ}$

Putting the value, we get -
$
\begin{gathered}
E_x=\frac{\lambda}{4 \pi \varepsilon_o r_o} \\
E_y=\frac{\lambda}{4 \pi \varepsilon_o r_o}
\end{gathered}
Recommended Topic Video

Solved Examples Based on Electric Field Due to an Infinite Line Charge

Example 1: A uniform non-conducting rod of mass $m$ and length $\underline{I}$, with density $\lambda$ is hinged at the midpoint at origin so that it can rotate in the horizontal plane. $\vec{E}$ is parallel to x-axis in the entire region. Calculate time period of oscillation.

1) $2 \pi \sqrt{\frac{m}{3 \lambda}}$
2) $2 \pi \sqrt{\frac{m}{3 \lambda E}}$
3) $2 \pi \sqrt{\frac{m}{\lambda}}$
4) $2 \pi \sqrt{\frac{m \lambda}{3 E}}$

Solution:

Line Charge

Electric field and Potential due to a charged straight wire length and charge density $\lambda$

wherein

$\begin{aligned} & \tau=\int_o^{\frac{1}{2}} d \tau_1+\int_o^{\frac{1}{2}} d \tau_2=2 \int_o^{\frac{1}{2}} E \lambda d x(\sin \Theta x)=\frac{E \lambda}{4} l^2 \sin \Theta \\ & \frac{M l^2}{12} \alpha=-\frac{E \lambda}{4} l^2 \Theta \Rightarrow T=2 \pi \sqrt{\frac{m}{3 E \lambda}}\end{aligned}$

Hence, the answer is option (2).

Example 2: Two semicircular wires $A B C$ and $A D C$ each of radius $r$ are lying in $\mathrm{X}-\mathrm{Y}$ plane and $\mathrm{X}-\mathrm{Z}$ plane. If $\lambda$ is linear charge density. Find $\vec{E}$ at origin.

1) $\frac{\lambda}{2 \pi \epsilon_o R} \hat{j}$
2) $-\frac{\lambda}{2 \pi \epsilon_o R}(\hat{i}+\hat{j})$
3) $-\frac{\lambda}{2 \pi \epsilon_o R}(\hat{j}+\hat{k})$
4) $\frac{\lambda}{2 \pi \epsilon_o R} \hat{k}$

Solution:

Electric field due to line charge

$
\begin{aligned}
& E_x=\frac{k \lambda}{r}(\sin \alpha+\sin \beta) \\
& E_y=\frac{k \lambda}{r}(\cos \beta-\cos \alpha)
\end{aligned}
$

Due to MA $=\frac{\lambda}{4 \pi \epsilon_o R}(\hat{i}-\hat{k})$
Due to $\mathrm{ADC}=\frac{\lambda}{2 \pi \epsilon_o R}(-\hat{k})$
Due to $\mathrm{NC}=\frac{\lambda}{4 \pi \epsilon_o R}(-\hat{i}+\hat{k})$
Due to $\mathrm{ABC}=\frac{\lambda}{2 \pi \epsilon_o R}(-\hat{j})$

Hence, the answer is option (1).

Example 3: The direction ${ }^{(\theta)}$ of $\vec{E}$ at point P due to uniformly charged finite rod will be:

1) $30^{\circ}$ from $X$
2) $45^{\circ}$ from $X$
3) $60^{\circ}$ from $X$
4) None

Solution:

If point P lies at Perpendicular bisector of wire

$\begin{aligned}
& \alpha=\beta \\
& E_x=\frac{2 k \lambda}{r} \sin \alpha \\
& E_y=0
\end{aligned}$

Using symmetry property

Hence, the answer is option (4).

Example 4: A long wire with uniform charge density $\lambda$ is bent in to given figure . Find E at point O .

1) 0
2) $\frac{\lambda}{4 \pi \epsilon_o R}$
3) $\frac{\sqrt{2} \lambda}{4 \pi \epsilon_o R}$
4) None

Solution:

1) 0

2) 

3) 

4) None

For segment 1

For segment 2

For segment 3

Field due to segment 1 is

$
\vec{E}_2=-\left[\frac{\lambda}{4 \pi \varepsilon_0 R}\right] \hat{i}+\left[\frac{\lambda}{4 \pi \varepsilon_0 R}\right] \hat{j}
$

Field due to quarter shape wire segment 3 is
$
\begin{aligned}
& \vec{E}_3=\left[\frac{\lambda}{4 \pi \varepsilon_0 R}\right] \hat{i}+\left[\frac{\lambda}{4 \pi \varepsilon_0 R}\right] \hat{j} \\
& E=E_1+E_2+E_3 \\
& E=\left[\frac{\lambda}{4 \pi \epsilon_o R}\right] \hat{i}+\left[\frac{\lambda}{4 \pi \epsilon_o R}\right] \hat{j} \\
& E_{\text {net }}=E=\frac{\sqrt{2} \lambda}{4 \pi \epsilon_o R}
\end{aligned}
$

Hence, the answer is option (3).

Example 5: A long wire of $\lambda$ charge density is bent into the given structure. Find $\vec{E}_{\text {net }}$ at point O.

1) 0
2) $\frac{\lambda}{2 \pi \epsilon_o R}$
3) $\frac{\sqrt{2} \lambda}{2 \pi \epsilon_o R}$
4) $\frac{\lambda}{4 \pi \epsilon_o R}$

Solution:

$\begin{aligned} & E=E_1+E_2+E_3 \\ & =\frac{\lambda}{4 \pi \epsilon_o R}[\hat{i}-\hat{j}]-\frac{\lambda}{4 \pi \epsilon_o R}[\hat{i}+\hat{j}]+\frac{\lambda}{2 \pi \epsilon_o R} \hat{j}=0\end{aligned}$

Summary

An electric field occurs radially outside a wire with an infinite length. Since the wire has a symmetrical aspect, its electrical field on any given point next to it depends on how far away one is from the wire but not from what point along its length. The intensity of this field is inversely proportional to distance.