Electric Field Lines - Definition, Properties, Attraction, FAQs

How to define a field or simply what does a field mean? ‘Field’ is a term referring to a quantity that is defined at every point in a space. The electric field at a point in the space around a charge or a system of charges gives us the force that a unit-positive test charge would experience, if it is placed at that point, without disturbing the system. Now, the work of the electric field lines is to map this electric field around a charge or a configuration of charges pictorially. So in this article, we will discuss what are electric field lines, electric field lines attraction and repulsion, properties of electric field lines class 12, rules for drawing electric field lines, electric field around a point charge, electric field between two-point charges, and differential equation of electric field lines and solved problems based on that.

This Story also Contains

1. Physical Significance of Electric Field
2. What are Electric Field Lines Class 12?
3. Electric Field Lines Attraction And Repulsion
4. Properties of Electric Field Lines Class 12
5. Rules For Drawing Electric Field Lines
6. Electric Field Around a Point Charge
7. Electric Field Between Two-Point Charges
8. Differential Equations for Electric Force Lines/Electric Field Lines
9. Solved Examples Based On Electric Field Lines

Physical Significance of Electric Field

As we have already discussed the electric field at a point in space around a system /configuration of electric charges tells us how a unit positive test charge would experience force at that particular point. Now, this field does not depend on the test charge we use to determine the electric field at that particular point. So we can say that by knowing the electric field at any point in space, we can calculate the magnitude and direction of force experienced by a unit test charge at that particular point. The direction of the electric field is outwards from a positive charge and it is directed inwards in case of a negative charge. Let $E$ be the electric field intensity at a point $\mathbf{r}$ and $q_0$ is the test charge, then $\mathbf{F}(\mathbf{r})=q_0 \mathbf{E}(\mathbf{r})$.This is the physical significance of the electric field.

What are Electric Field Lines Class 12?

Electric field lines definition: Electric field lines are the imaginary lines that signify the direction and strength of an electric field. The electric field lines are discovered by Michael Faraday. Electric field lines are nothing but the path along which a unit positive charge will move if it is placed there and allowed to be free to move.

An electric field around a charge or a configuration of charges can be mapped pictorially using the electric field lines, also called the electric lines of forces. It is a mathematical way of visualizing electric fields around a charge or a system of charges placed in a particular configuration. However, for electric field lines definition, we can define an electric field line as a path, which can be curved or straight, in an electric field, such that tangent to it at any point gives us the direction of the electric field at that point.

The figure given below is an electrostatic line of force. The tangent to the line at point P gives us the direction of the electric field $E_{p}$ and similarly, the tangent to the curved line at point R gives us the direction of the electric field intensity.

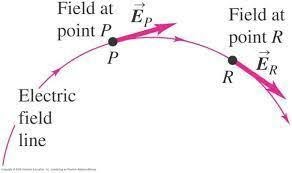
(Fig-1)

Thus, electric field lines provide information about the direction of electric field intensity at a point. Also, the magnitude of the electric field is represented by the density of field lines or the number of electric lines of force in that region. The denser the region with field lines; the greater the magnitude of electric field intensity at that region. Note that these field lines are in all three dimensions.

Electric Field Lines Attraction And Repulsion

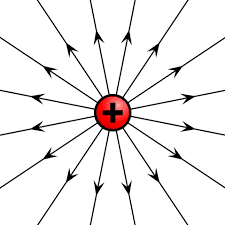
• The figure shows electric field lines/lines of forces due to a single positive charge. Note the direction of electric field lines. These lines for a single positive point charge are directed radially outwards and extend up to infinity.

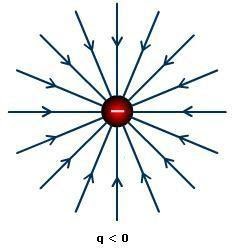
However, in the case of a single negative point charge, the electric field lines are always directed radially inwards.

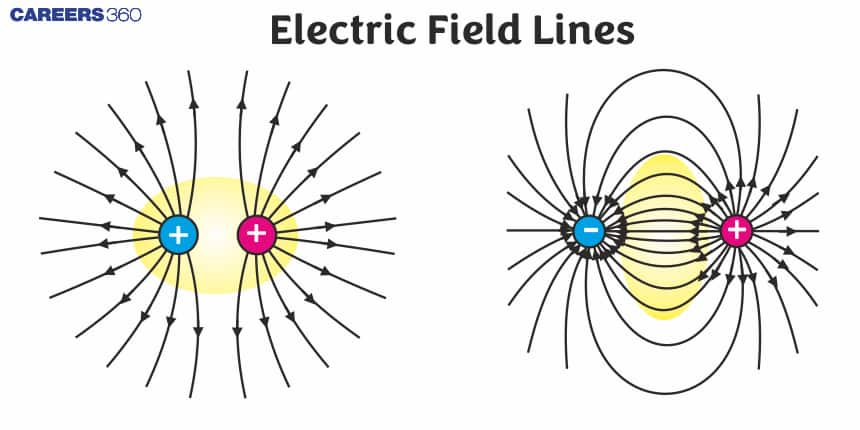
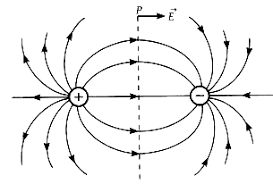
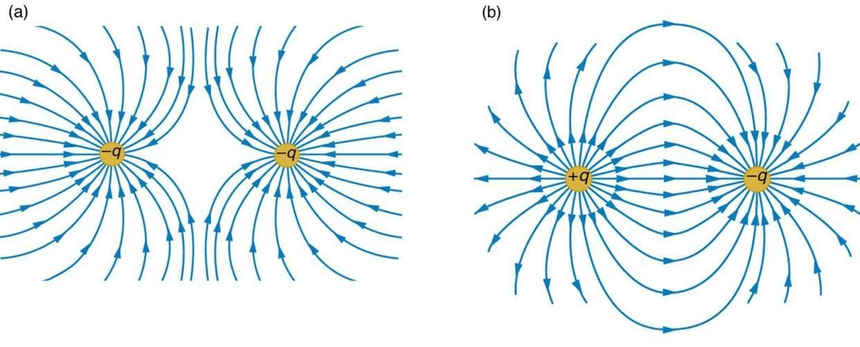
• The figure below shows the electric field lines for a pair of equal and opposite charges, also called an electric dipole. Note the direction of the electric field, it goes from positive to negative charge. These electric field lines show that there is a mutual attraction between the two opposite charges. Hence these are the attractive field lines between the charges.

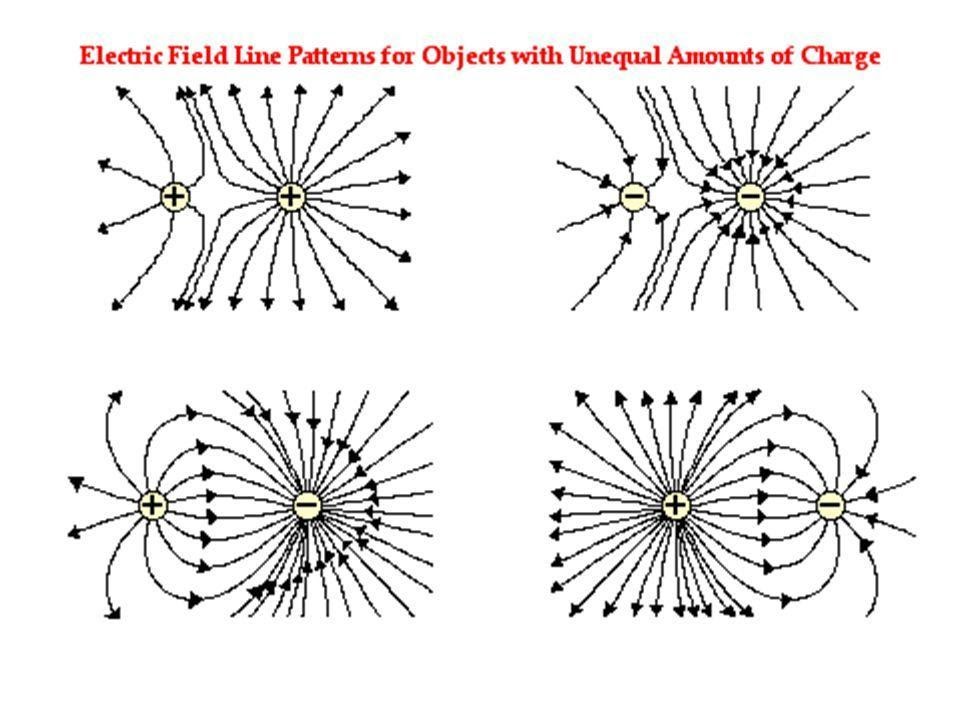
• The figure given below shows electric field lines for opposite and unequal charges. The electric field lines are always denser towards the charge having a larger magnitude.

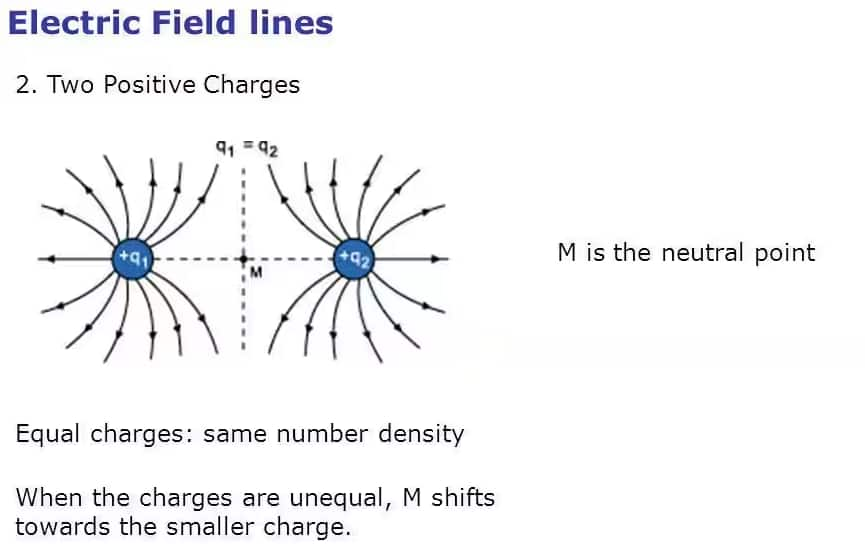
• The figure given below shows electric field lines due to two equal positive charges. These field lines are repulsive. These lines exert lateral pressure on each other and this results in repulsion between the charges. Also, note that there is a neutral point exactly at the middle (point M) where net electric field intensity is equal to zero.

• Similarly, electric field lines are due to two equal negative charges.

• This neutral point shifts from the center position if the charges are unequal where this neutral point is closer to the smaller charge

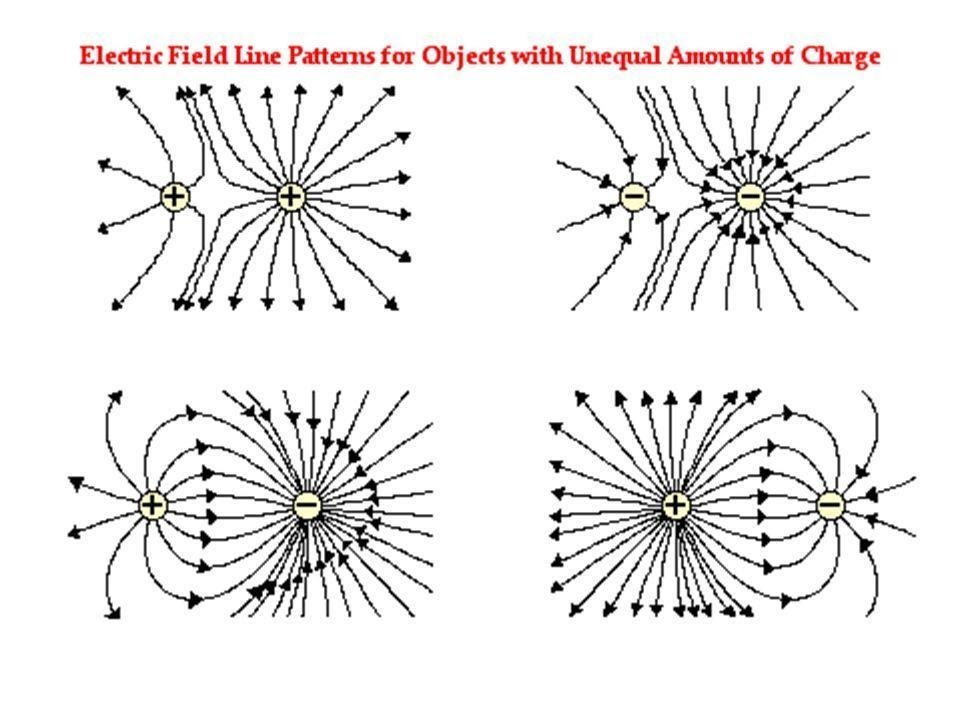
• Some other miscellaneous cases such as the representation of the field lines due to 2 equal positively charged rods normal to the page and due to two rods of linear charge density 2 and $-\lambda$ respectively, normal to the page.

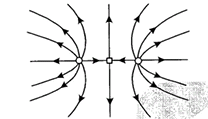
The box denotes the neutral point where the electric field is zero.

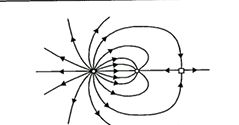
Properties of Electric Field Lines Class 12

The properties of electric field lines are-

1. Electric field lines are always continuous. They are continuous curves but they do not form loops. They start from a positive charge or a positively charged body and end at a negative charge or a negatively charged body. In the case of a single positive and negative charge, the electric field lines end or start at infinity.

2. The tangent to an electric field line at any point gives us the direction of the electric field at that particular point.

3. Two electric field lines of force never intersect with each other. The reason behind this is, that if two lines intersect with each other, then at that intersecting point, we can draw 2 tangents which will give two directions of electric fields $E_1$ and $E_2$ which is not possible. Hence, two electric field lines will never intersect with each other.

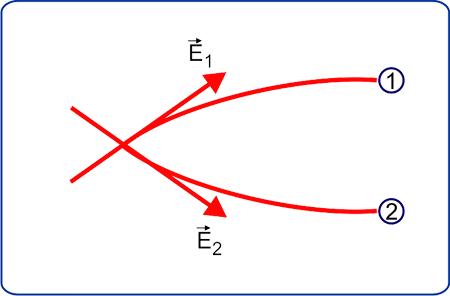
4. The electric field lines exert a lateral pressure in case of repulsion between like charges.

5. The electric field lines contract longitudinally in case of attraction between opposite charges.

6. No component of the electric field is parallel to the surface of the conductor. They are always perpendicular to the surface of a conductor.

Rules For Drawing Electric Field Lines

1. The electric field lines direct away from positive charges and towards negative charges.
2. The electric field lines begin on positive charges and end on negative charges.
3. If there is no end opposite charge, they end at infinity
4. The electric field lines should never cross each other
5. No closed loop because electric field lines don't form closed loops
6. The lines are closer when the field is stronger

Electric Field Around a Point Charge

The electric field around a point charge is experienced in a region around a charge where it exerts force on other charges. The magnitude of the charge and the distance from the charge are the two factors affecting the field strength. The electric field at a distance $r$ of a point charge $q$ is

$$
E=\frac{k|Q|}{r^2}
$$

where,

$E$ is the electric field strength
$Q$ is the magnitude of the point charge
$r$ is the distance from the charge
$k$ is the coulomb's constant

Electric Field Between Two-Point Charges

If the electric field at a point due to $Q_1$ is $E_1=\frac{k\left|Q_1\right|}{r_1^2}$ and due to $Q_2$ is $E_2=\frac{k\left|Q_2\right|}{r_2^2}$, then the total electric field $E$ at that point is:

$$
E=E_1+E_2=\frac{k\left|Q_1\right|}{r_1^2}+\frac{k\left|Q_2\right|}{r_2^2}
$$

where,

$E$ is the total electric field at the point
$r_1$ is the distance from $Q_1$ to the point
$r_2$ is the distance from $Q_2$ to the point
$k$ is the coulomb's constant

Differential Equations for Electric Force Lines/Electric Field Lines

Suppose $\mathbf{r}=\mathbf{r}(s)$ represents the force lines. Then, $\frac{d \mathbf{r}}{d s}$ will represent the tangent to the force line at every point. Since the tangent to the curve at any point represents the direction of the electric field, therefore,

$$
\frac{d \mathbf{r}}{d s}=\alpha \mathbf{E}(\mathbf{r})
$$

$
\text { where } \alpha \text { is a constant. }
$

$\begin{gathered}\frac{d x}{d s}=\alpha E_x, \quad \frac{d y}{d s}=\alpha E_y, \quad \frac{d z}{d s}=\alpha E_z \\ \frac{d x}{E_x}=\frac{d y}{E_y}=\frac{d z}{E_z}\end{gathered}$

This is the differential equation for electric field lines.

Also, read

• NCERT Exemplar Solutions for All Subjects
• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects

Recommended Topic Video

Solved Examples Based On Electric Field Lines

Example 1: A long cylindrical shell carries a positive surface charge $\sigma$ in the upper half and a negative surface charge $-\sigma$ in the lower half. The electric field lines around the cylinder will look like the figure given in : (figures are schematic and not drawn to scale)

1)

2)

3)

4)

Solution:

Direction of Electric field -Due to a Positive Charge electric field is always away from the charge.

Direction of Electric field

Due to the Negative charge electric field is always towards the charge.

The electric field lines around the cylinder must resemble that due to the dipole.

Example 2: Charges are placed on the vertices of a square as shown. Let {E}$ be the electric field and V the potential at the center. If the charges on A and B are interchanged with those on D and C respectively, then

1) $\vec{E}$ changes, V remains unchanged

2) $\vec{E}$ remains unchanged $V$ changes

3) both $\vec{E}$ and $V$ change

4) both $\vec{E}$ and $V$ are unchanged

Solution:

Direction of Electric field

Due to the Positive Charge electric field is always away from the charge.

Direction of Electric field

Due to the Negative charge electric field is always towards the charge.

"Unit positive charge" will be repelled by A and B and attracted by -q and -q downwards in the same direction. If they are exchanged the direction of the field will be opposite. In the case of potential, as it is a scalar, they cancel each other whatever may be their position.

$\therefore$ The field is affected but not the potential.

Example 3: A charged particle is free to move in an electric field. It will travel

1) Always along a line of force

2) Along a line of force, if its initial velocity is zero

3) Along a line of force, if it has some initial velocity in the direction of an acute angle with the line of force

4) None of the above

Solution:

Because E points along the tangent to the lines of force. If the initial velocity is zero, then due to the force, it always moves in the direction of $E$. Hence it will always move on some lines of force.

Hence, the answer is the option (2).

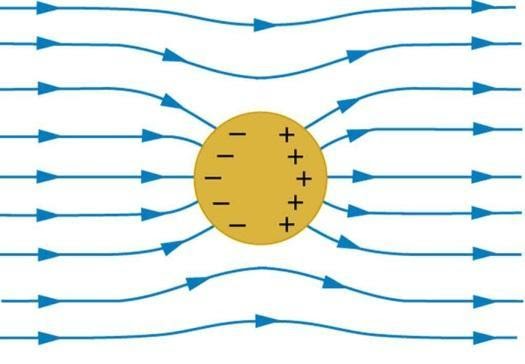
Example 4: A metallic solid sphere is placed in a uniform electric field. The lines of force follow the path(s) shown in the figure as

1) 1

2) 2

3) 3

4) 4

Solution:

Direction of Electric field

Due to the Positive Charge electric field is always away from the charge.

The electric field is always perpendicular to the surface of a conductor. On the surface of a metallic solid sphere, the electrical field is oriented normally (i.e. directed towards the center of the sphere).

Example 5: Electric lines of force about negative point charge are

1) Circular, anticlockwise

2) Circular, clockwise

3) Radial, inward

4) Radial, outward

Solution:

Direction of Electric field

Due to the Positive Charge electric field is always away from the charge.

Electric lines' force due to negative charge is radially inward.