Electric potential due to an electric dipole

Wonder what the electric potential does around different configurations of charges? Two especially interesting cases are those of the electric potential of a dipole—a pair of opposite charges close together—and of the potential of many charges. These two configurations produce distinctive electric fields that alter the potential at various points around them. These will be important in understanding electric fields and their potential from molecular chemistry to electrical engineering applications. So, let us consider these: electric potential due to a dipole and a system of charges.

In this article, we will cover the concept of the Electric Potential Of A Dipole And the System Of Charges. This concept is in the Electrostatics chapter which is an important chapter in class 12th physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE and more.

Electric Potential Due to an Electric Dipole at a Point on the Axial Line

As shown in the above figure We want to find out the Electric Potential due to an Electric Dipole at Point M which is on an axial line and at a distance r from the centre of a dipole.

Where V1 and V2 is the Electric Potential at M due to −q and +q charges respectively?

Using P=q(2a)
So Vnet=kPr2−a2
V1=kq(r+a)V2=kq(r−a)Vnet =V2−V1Vnet =V1+V2=−kq(r+a)+kq(r−a)=kq{1r−a−1r+a}=kq{(r+a)−(r−a)(r−a)(r+a)} So Vnet =2kqar2−a2

• if r>>a
  then
  Vnet =KPr2=P4πϵ0r2

Electric potential due to an Electric Dipole at a Point on the Equatorial line

As shown in the above figure We want to find out Electric potential due to an Electric Dipole at Point M which is on the Equatorial line and at a distance r from the center of a dipole.

Where V1 and V2 is the Electric Field Intensity at M due to −q and +q charges respectively?

V1=−14πϵ0∗qr2+a2V2=14πϵ0∗qr2+a2Vnet =V2−V1=0

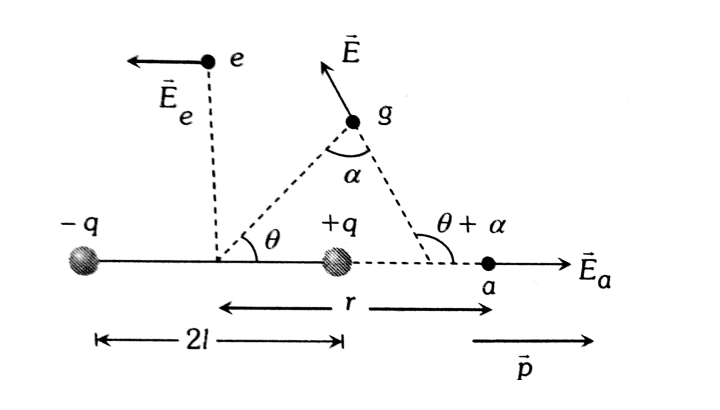
Electric potential due to a dipole at any general point

As shown in the above figure We want to find out the Electric potential due to an Electric Dipole at Point M which at a distance r from the center of a dipole and making an angle θ with the axial line.

From the figure, M is at the axial line of dipole having dipole moment as Pcos⁡θ and M is at the Equatorial line of dipole having dipole moment as Psin⁡θ.

So Psin⁡θ has no contribution in electric potential at point M .

if r>>a

if r>>a
then Va=14πε0×2Pcos⁡θr2 and V⊥=0
So Vnet=Va=KPcos⁡θr2

Recommended Topic Video

Solved Example Based On Electric Potential Of A Dipole And System Of Charges

Example 1: If the magnitude of the intensity of the electric field at a distance x on the axial line and, at a distance y on the equatorial line on a given dipole are equal, then x:y is

1) 1:1
2) 1:2
3) 1:2
4) 23:1

Solution:

The ratio of the magnitude of intensity of the electric field on the axial line and the equational line is given as,
EaEe=k×2px3k×py3
Or,
xy=(21)13
Thus, the ratio \( x:y \) is \( \sqrt[3]{2}: 1 \).

Example 2: An electric dipole is placed along the x-axis at the origin O. A point P is at a distance of 20 from this origin such that OP makes an angle π/3 with the x-axis. If the electric field at P makes an angle θ with the x-axis, the value of θ would be

1) π/3
2) π/3+tan−1⁡(32)
3) 2π3
4) tan−1⁡(32)

Solution:

As we have learned

Electric Field and Potential Due to an Electric Dipole -

At axial point

Eazial =2kpr(r2−l2)2Vaxial =kP(r2−l2)

- wherein

θ=π/3+α.. where.. tan⁡α=1/2tan⁡π/3

Example 3: An electric dipole is placed along the x-axis at the origin O. A point P is at a distance of 20 from this origin such that OP makes an angle pi/3 with the x-axis. If the electric field at P makes an angle θ with the x-axis, the value of θ would be:

1) π/3
2) π/3+tan−1⁡(32)
3) 2π3
4) tan−1⁡(32)Solution:

As we have learned

Electric Field and Potential Due to an Electric Dipole -

At axial point

Eazial =2kpr(r2−l2)2Vaxial =kP(r2−l2)

- wherein

θ=π/3+α.. where.. tan⁡α=1/2tan⁡π/3

Example 4: Charge −q and +q located at A and B, respectively, constitute an electric dipole. Distance AB=2a,O is the mid point of the dipole and OP is perpendicular to AB. A charge Q is placed at P where OP=y and y>>2a. The charge Q experiences an electrostatic force F . If Q is now moved along the equational line to P′ such that OP′=(y3), the force on Q will be close to: (y3>>2a),

1)9F

2)27 F

3)F/3

4)3F

Solution:

The electric field of the equatorial plane of the dipole =−kp→r3
At P,F=−KP→Qr3

At P′,

F′=−KP→Qr33=27F

Example 5: The electric field at a point on the equatorial line of a dipole and the direction of the dipole moment

1)Will be parallel

2) Will be in the opposite direction

3)Will be perpendicular

4)Are not related

Solution: The direction of the electric field at the equatorial point will be in the opposite direction, as that of the direction of the dipole moment.

∴E→=−p→4πϵ0(r2+a2)3/2

The angle between Eequi and p→ is 180∘.

Summary

Electric potential due to a dipole, consisting of two opposite charges separated by a small distance, varies with position, being strongest next to the charges. For many charges, the electric potential at a point will be the sum of the potentials due to the individual positions of the charges. These potentials are of utility in the analysis of complex electric fields and of importance with applications in physics and chemistry.