Energy In Simple Harmonic Motion

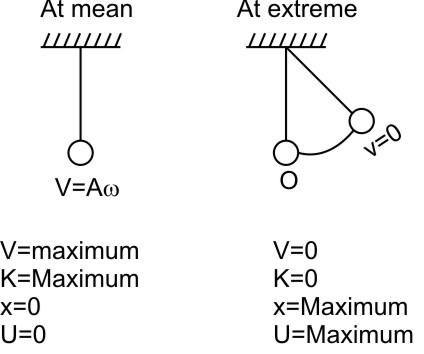
Energy in simple harmonical motion (SHM), oscillates between kinetic and potential forms showing us basic physics principles. In the simple harmonic motion, an object experiences a force that pushes it back towards the equilibrium point and this makes it move up and down. At one extreme position, potential energy reaches its maximum point; however, the kinetic energy here is equal to zero whereas when the body is at mid-point it has higher kinetic energy but minimalizing potential energy.

This Story also Contains

1. What is Potential Energy?
2. What is Kinetic Energy?
3. Total Energy
4. Graph of Energy in S.H.M
5. Solved Examples Based on Energy in SHM
6. Summary:
7. Frequently Asked Questions (FAQs):

In this article we will discuss how energy operates during simple harmonic motion (SHM) involves knowing the physics basics and has far-reaching applications towards preparing for competitive examinations such as the National Eligibility cum Entrance Test (NEET), or Joint Entrance Examination (JEE). It depicts the movement of vibrating systems, for instance, springs or pendulums, which play an integral role in different physical occurrences.

A particle executing S.H.M. possesses two types of energy: Potential energy and Kinetic energy

What is Potential Energy?

This is an account of the displacement of the particle from its mean position.

$\text{As restoring force is given as}F=-kx$

$\begin{array}{rl}& U=-\int dw=-{\int }_0^{x}Fdx={\int }_0^{x}kxdx=\frac{1}{2}k{x}^2\\ & \text{using}\omega =\sqrt{\frac{k}{m}}\text{or}k=m{\omega }^2\\ & \text{we get}U=\frac{1}{2}m{\omega }^2{x}^2\\ & \text{For}x=A\sin (wt)\\ & U=\frac{1}{2}m{\omega }^2{A}^2{\sin }^2\omega t\end{array}$

Potential energy maximum and equal to total energy at extreme positions

i.e

$U_{max}=\frac{1}{2}k{A}^2=\frac{1}{2}m{\omega }^2{A}^2\text{when}x=\pm A;\omega t=\pi /2;t=T/4$

Potential energy is minimum at the mean position

$\text{i.e}{U}_{min}=0\text{when}x=0;\omega t=0;t=0$

The average value of potential energy with respect to t

Average of $U=\frac{\int Udt}{\int dt}$
$\because U=\frac{1}{2}k{x}^2$

So

$U_{\text{avg}}=\frac{\int \frac{1}{2}m{\omega }^2{A}^2{\sin }^2\omega t}{\int dt}=\frac{\int \frac{1}{4}m{\omega }^2{A}^2(1-\cos 2\omega t)dt}{dt}=\frac{1}{4}m{\omega }^2{A}^2$

What is Kinetic Energy?

This is because of the velocity of the particle.

Formula

$K=\frac{1}{2}m{v}^2$

$\text{or using}v=A\omega \cos \omega t\text{we get}K=\frac{1}{2}m{A}^2{\omega }^2{\cos }^2\omega t$

And using $v=w\sqrt{A^2-x^2}$ and $k=m{\omega }^2$ we get $K.E.=\frac{1}{2}K(A^2-x^2)$

Kinetic energy is maximum at the mean position and equal to total energy at the mean position.

$\text{i.e}{K}_{max}=\frac{1}{2}m{\omega }^2{A}^2\text{when}x=0;t=0;\omega t=0$

Kinetic energy is minimum at the extreme positions.

$\text{i.e}{K}_{min}=0\text{when}y=A;t=T/4,\omega t=\pi /2$

The average value of kinetic energy with respect to t

$\begin{array}{c}{K}_{avg}=\frac{\int Kdt}{\int dt}\\ K_{avg}=\frac{\int \frac{1}{2}m{\omega }^2{A}^2{\cos }^2(\omega t)}{\int dt}=\frac{\int \frac{1}{4}m{\omega }^2{A}^2(1+\cos 2\omega t)dt}{dt}=\frac{1}{4}m{\omega }^2{A}^2\end{array}$

$\text{So}{K}_{avg}=U_{avg}$

Total Energy

Total mechanical energy = Kinetic energy + Potential energy or E=K+U

$E=\frac{1}{2}m{\omega }^2(A^2-x^2)+\frac{1}{2}m{\omega }^2{x}^2=\frac{1}{2}m{\omega }^2{A}^2$

So Total energy does not depend on position(x) i.e. it always remains constant in SHM.

Graph of Energy in S.H.M

At time t=0 sec, the position of the block is equal to the amplitude,

Recommended Topic Video

Solved Examples Based on Energy in SHM

Example 1: For a simple pendulum, a graph is plotted between its kinetic energy (KE) and potential energy (PE) against its displacement d. Which one of the following represents these correctly?

(graphs are schematic and not drawn to scale)

1)

2)

3)

4)

Solution:

The kinetic energy in S.H.M.

$\begin{array}{rl}& K\cdot E\cdot =\frac{1}{2}m{u}^2\\ & =\frac{1}{2}m(A^2-x^2){\omega }^2\end{array}$
wherein
$\begin{array}{rl}& K.E.=\frac{1}{2}k(A^2-x^2)\\ & k=m{\omega }^2\end{array}$

For a simple pendulum variation, K.E. and P.E. with displacement d is

$\begin{array}{rl}& K.E.=\frac{1}{2}m{\omega }^2(A^2-d^2)\\ & P.E.=\frac{1}{2}m{\omega }^2{d}^2\\ & \text{if}d=0K.E.=\frac{1}{2}m{\omega }^2{A}^2\text{P.E.}=0\\ & \text{if}d\pm A\text{K.E.}=0\text{P.E.}=\frac{1}{2}m{\omega }^2{A}^2\end{array}$

Graph 2 represents the variation correctly.

Hence, the answer is option (2).

Example 2: In a simple harmonic oscillator, at the mean position

1) kinetic energy is minimum, and potential energy is maximum

2) both kinetic and potential energies are the maximum

3) kinetic energy is maximum, and potential energy is minimum

4) both kinetic and potential energies are minimal.

Solution:

The kinetic energy in S.H.M. -

$\begin{array}{rl}& K.E.=\frac{1}{2}m{u}^2\\ =& \frac{1}{2}m(A^2-x^2){\omega }^2\end{array}$

Potential energy in S.H.M. -

$\text{P.E.}=\frac{1}{2}K{x}^2$

Hence, K.E. is maximum and P.E. is minimum at the mean position.

Hence, the answer is option (3).

Example 3: A body executes simple harmonic motion. The potential energy (P.E.), the kinetic energy (K.E.) and total energy (T.E.) are measured as a function of displacement x. Which of the following statements is true?

1) K.E. is maximum when $x=0$
2) T.E. is zero when $x=0$
3) K.E. is maximum when $x$ is maximum
4) P.E. is maximum when $x=0$

Solution:

The kinetic energy in S.H.M.

$\begin{array}{c}K\cdot E\cdot =\frac{1}{2}m{u}^2\\ =\frac{1}{2}m(A^2-x^2){\omega }^2\\ K\cdot E\cdot =\frac{1}{2}K(A^2-x^2)\\ K=m{\omega }^2\end{array}$

We know that
$\begin{array}{rl}& K=\frac{1}{2}m{\omega }^2(A^2-x^2)\\ & \text{If}x=0\\ & K=\frac{1}{2}m{\omega }^2{A}^2=\text{Maximum}\end{array}$

i.e. when x = 0 K.E. is maximum.

Hence, the answer is the option (1).

Example 4: Starting from the origin, a body oscillates simply harmonically with a period of 2 s. After what time will its kinetic energy be 75% of the total energy -

1) $\frac{1}{12}\mathrm{s}$
2) $\frac{1}{6}\mathrm{s}$
3) $\frac{1}{4}s$
4) $\frac{1}{3}s$

Solution:

The kinetic energy in S.H.M.

$\begin{array}{c}K\cdot E.=\frac{1}{2}m{u}^2\\ =\frac{1}{2}m(A^2-x^2){\omega }^2\end{array}$

wherein

$\begin{array}{rl}& K.E.=\frac{1}{2}k(A^2-x^2)\\ & k=m{\omega }^2\\ & \end{array}$

During simple harmonic motion, Kinetic energy
$=\frac{1}{2}m{\nu }^2=\frac{1}{2}m(a\omega \cos \omega t{)}^2$

Total energy $E=\frac{1}{2}m{a}^2{\omega }^2$
$\because ($ Kinetic energy $)=\frac{75}{100}(E)$
or $\frac{1}{2}m{a}^2{\omega }^2{\cos }^2\omega t=\frac{75}{100}\times \frac{1}{2}m{a}^2{\omega }^2$
or ${\cos }^2\omega t=\frac{3}{4}\Rightarrow \cos \omega t=\frac{\sqrt{3}}{2}=\cos \frac{\pi }{6}$
$\therefore \omega t=\frac{\pi }{6}$
or $t=\frac{\pi }{6\omega }=\frac{\pi }{6(2\pi /T)}=\frac{2\pi }{6\times 2\pi }=\frac{1}{6}s$

Hence, the answer is the option (2).

Example 5: The kinetic energy and potential energy of a particle executing simple harmonic motion will be equal when displacement (amplitude = a) is:

1) $\frac{a}{2}$
2) $a\sqrt{2}$
3) $\frac{a}{\sqrt{2}}$
4) $\frac{a\sqrt{2}}{3}$

Solution:

The kinetic energy in S.H.M.

$K.E.=\frac{1}{2}m{v}^2=\frac{1}{2}m(A^2-x^2){\omega }^2$
wherein
$\begin{array}{rl}& K.E.=\frac{1}{2}k(A^2-x^2)\\ & k=m{\omega }^2\end{array}$

Suppose at a displacement $y$ from the mean position,
$\begin{array}{rl}& \text{Potential energy}=\text{Kinetic energy}\\ & \frac{1}{2}m(a^2-y^2){\omega }^2=\frac{1}{2}m{y}^2{\omega }^2\\ & \Rightarrow a^2=2y^2\Rightarrow y=\frac{a}{\sqrt{2}}\end{array}$

Hence, the answer is the option (3).

Summary:

"Simple harmonic motion" or "simple harmonic oscillation" refers to a harmonic oscillation with a unique frequency and specified amplitude. When a particle exhibits S.H.M., its displacement and velocity give rise to both potential and kinetic energy, respectively.

The total energy of a particle of mass m is given by:

$E=\frac{1}{2} m \omega^{2} A^{2}$

Frequently Asked Questions (FAQs):

Q 1: What are the characteristics of S.H.M.?

Ans:

• In linear S.H.M., the particle moves to and fro, with respect to the fixed mean position, in a straight line.
• A restoring force acts on the particle, which varies directly with the particle’s displacement from the mean position.
• The restoring force’s direction is always towards the mean position.

Q 2. What is the total mechanical energy in SHM?

Ans: The total mechanical energy (E) in SHM is the sum of kinetic energy (KE) and potential energy (PE) and remains constant. It is given by: $E=\frac{1}{2}k{A}^2$ where k is the spring constant and A is the amplitude of oscillation.

Q 3. How does the kinetic energy (KE) vary in SHM?

Ans: The kinetic energy KE in SHM varies with displacement x and is given by:$KE = \frac{1}{2} m \omega^2 (A^2 - x^2)$ where mmm is the mass, ω is the angular frequency, and A is the amplitude.

Q 4. What is the potential energy (PE) in SHM?

Ans: The potential energy PE in SHM for a mass-spring system at a displacement xxx is given by:$PE = \frac{1}{2} k x^2$ where k is the spring constant and x is the displacement from the equilibrium position.