Energy Stored in a Capacitor - A Complete Guide

Q: Let suppose a condenser is charged to 5 ?f is now doubled ,then what would be the change in Energy stored 1 Remains same 2 Becomes two times 3 Becomes four times 4 Becomes half

As we know, E=Q 2 /2c, thus E&prop;Q 2 Hence on doubling the value of Q, Energy stored becomes 4 times. Hence the correct option is (3).

Edited By Vishal kumar | Updated on Jul 02, 2025 04:49 PM IST

Imagine a camera flash. If you press the button, it produces light. The flash requires additional energy to produce that light. This energy is stored in a Capacitor inside the camera. the capacitor charges up when it is connected to the battery and energy is stored in it and then gives out all energy, thus creating the flash. In this article, we will study Capacitor and its working. We will also study the expression of energy stored in capacitors. In the later part, we will derive the equation of energy stored in a capacitor followed by work done by the capacitor.

This Story also Contains

What is a capacitor?
Formula for Capacitance
Working of Capacitor
Application of Capacitor

Energy Stored in a Capacitor - A Complete Guide

What is a capacitor?

A capacitor is a device consisting of two conductive plates separated by an insulating material known as a Dielectric. Basically, it is an electric component that stores charge in the form of an electric field.

SI unit of Capacitance (C)

Capacitance is measured in farads (f).

1 farad ( $F$ ) is defined as the capacitance of a capacitor that, when charged with 1 coulomb ( $C$ ) of electric charge, results in a potential difference of 1 volt $(\mathrm{V})$ across its plates:

$$
1 \mathrm{~F}=\frac{1 \mathrm{C}}{1 \mathrm{~V}}
$$

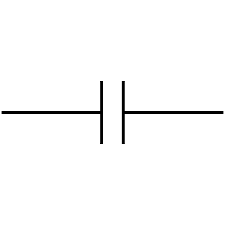
Capacitor

Formula for Capacitance

Thus capacitance is given by the formula:

$$
\mathrm{C}=\mathrm{q} / \mathrm{V}
$$
Where,

$q=$ charge develop on each plate
$\mathrm{V}=$ voltage between them

Working of Capacitor

It works on principles of Coulomb’s law in which like charges repel each other while unlike charges attracts each other thus unlike charge polarity gets induced on the inside surfaces of charged plates of a capacitor. The conductor thus holds equal and opposite charges inside the surface and thus the formation of electric field inside the non-conducting region.

Here's a simple breakdown of how Capacitor works:

Charging: When it gets connected to a power source, one plate gains a positive charge and the other one gets a negative charge. This creates an electric field between the plates, storing energy.
Storing energy: These plates hold this energy in the electric field as long as it is connected to a power source.
Discharging: When disconnected from the source and connected to a circuit, the stored energy flows out, creating a current until the plates have an equal charge.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Related Topics

Derive the expression for energy stored in a capacitor

Capacitors not only store charge but store energy as well thus when it is connected to the circuit there is decrease in charge as well as transfer of charge takes place.

Consider a parallel plate capacitor. Let C be the capacitance at time t. Charge on the capacitor and the potential difference between capacitor plates is zero. Potential difference increases when the charge is given. Then potential difference between its plate is V=q/C where q is the charge at any instant.

Work done in providing more charge is given by:

$$
\begin{aligned}
& \mathrm{dW}=\mathrm{Vdq} \\
& \mathrm{dW}=\mathrm{dq} \mathrm{q} / \mathrm{C}
\end{aligned}
$$

On integrating the equation from 0 to 1 , $\mathrm{E}=\mathrm{Q}^2 / 2 \mathrm{C} \quad$ (Work Done)

We know that charge, $\mathrm{Q}=\mathrm{CV}$
Total energy stored in the capacitor,

$$
\begin{aligned}
& \mathrm{E}=\mathrm{Q}^2 / 2 \mathrm{C} \\
& \mathrm{E}=\mathrm{CV}^2 / 2 \\
& \mathrm{E}=\mathrm{QV} / 2
\end{aligned}
$$

Work done by the capacitor

Work done by the capacitor to accumulate charge inside it is equal to Energy stored inside the capacitor.

Or it is given by

$\mathrm{W}=\mathrm{Cv}^2 / 2$

Power of the capacitor

We can determine Power of the capacitor by multiplying the voltage (V) across terminals and current(I), or

$\mathrm{P}=\mathrm{VI}$

Application of Capacitor

Capacitor has been widely used as a storage device for the energy produced.
It can be used as a dissipated battery, as it stores energy when connected to the circuit and delivers that energy when it gets disconnected from the circuit.
Large capacitors are used in industrial power systems to improve power factor, reducing energy losses and improving efficiency.
Capacitors are used to improve the power factor and minimize energy loss.
Capacitors give a kick-start in some low-voltage appliances like fans, and compressor electric motors.

Frequently Asked Questions (FAQs)

1. Let suppose a condenser is charged to 5 ?f is now doubled ,then what would be the change in Energy stored 1 Remains same 2 Becomes two times 3 Becomes four times 4 Becomes half

As we know, E=Q²/2c, thus E∝Q²

Hence on doubling the value of Q, Energy stored

becomes 4 times. Hence the correct option is (3).

2. When a capacitor is disconnected from the battery after charging, then what happens to electric Potential energy and potential difference? Which of the following statements is correct?

1 Both Electric potential energy and potential difference decreases.

2 Electric potential remains the same and potential difference increases.

3 Electric Potential remains the same and the potential difference decreases.

4 Both Electric Potential energy and Potential difference increases.

We know, when the capacitor is disconnected then there is flow of charge and Electric Potential Energy remains the same , as charge keeps on decreasing so does potential difference. Hence the correct answer is option(3).

3. Define capacitor energy.

Capacitor energy is the work by which the capacitor gets charged.

4. Capacitor stores which type of energy?

Electrical potential energy

5. Write the relation between q, c, and v.

Capacitance, C=q/V

Where, q= charge develop on each plate

V= voltage between them

6. What is the SI unit of charge?

Coulomb

7. What are the different types of capacitors?

Mica capacitor, film capacitor, ceramic capacitor, paper capacitor etc.

8. Why don't we use capacitors instead of batteries for long-term energy storage?

Capacitors are not typically used for long-term energy storage because they have a much lower energy density compared to batteries. They also tend to self-discharge more quickly, making them less suitable for applications requiring long-term energy storage.

9. What happens to the energy stored in a capacitor when it's discharged?

When a capacitor is discharged, the stored electrical potential energy is converted into other forms of energy, such as heat in a resistor, light in an LED, or mechanical energy in a motor, depending on the circuit it's connected to.

10. How does the energy stored in a capacitor compare to the energy stored in a battery?

Capacitors typically store less total energy than batteries but can release their energy much more quickly. Batteries store chemical energy that is converted to electrical energy, while capacitors store energy directly in an electric field.

11. How is the energy density of a capacitor defined?

Energy density for a capacitor is defined as the amount of energy stored per unit volume or per unit mass. It's an important parameter for comparing different energy storage devices and is typically measured in joules per cubic meter (J/m³) or joules per kilogram (J/kg).

12. How does temperature affect the energy storage capacity of a capacitor?

Temperature can affect a capacitor's energy storage capacity by changing its capacitance and maximum voltage rating. High temperatures can reduce the maximum voltage a capacitor can withstand, potentially decreasing its maximum energy storage capacity.

13. What happens to the energy stored in a capacitor if its capacitance is doubled?

If the capacitance is doubled while keeping the voltage constant, the energy stored will also double. This is because energy is directly proportional to capacitance when voltage is held constant.

14. How does the dielectric material affect the energy stored in a capacitor?

The dielectric material increases the capacitance of the capacitor, allowing it to store more charge at a given voltage. This, in turn, increases the energy that can be stored. The dielectric constant of the material directly affects how much the capacitance, and thus the energy storage, increases.

15. What's the relationship between the electric field strength and the energy stored in a capacitor?

The energy stored in a capacitor is proportional to the square of the electric field strength between its plates. This relationship is expressed as E = 1/2 ε₀εᵣE²V, where ε₀ is the permittivity of free space, εᵣ is the relative permittivity of the dielectric, E is the electric field strength, and V is the volume between the plates.

16. Can the energy stored in a capacitor be negative?

No, the energy stored in a capacitor cannot be negative. Energy is a scalar quantity and is always positive or zero. Even when a capacitor is charged with opposite polarity, the stored energy remains positive.

17. Can a capacitor store more energy than the work done to charge it?

No, a capacitor cannot store more energy than the work done to charge it. The energy stored in the capacitor is exactly equal to the work done by the charging source, assuming no energy losses in the process.

18. What's the difference between electrostatic energy and the energy stored in a capacitor?

Electrostatic energy refers to the potential energy of any static electric charge configuration. The energy stored in a capacitor is a specific form of electrostatic energy, where the charge configuration is constrained to two conductors (the plates) separated by a dielectric.

19. How is the concept of energy stored in a capacitor related to lightning?

Lightning can be thought of as a natural capacitor discharge. The earth and the clouds act as the two plates of a capacitor, with the air in between serving as the dielectric. The enormous energy released in a lightning strike is analogous to the rapid discharge of a capacitor.

20. What's the difference between energy and charge in a capacitor?

Charge (measured in coulombs) is the amount of excess electrons on one plate and deficit on the other. Energy (measured in joules) is the work required to separate these charges against the electric field. While charge increases linearly with voltage, energy increases quadratically.

21. How does the shape of the capacitor plates affect energy storage?

The shape of the capacitor plates doesn't directly affect energy storage. However, it can affect the capacitance, which in turn affects energy storage. Shapes that maximize surface area while minimizing separation (like interleaved plates) can increase capacitance and thus energy storage capacity.

22. Can the energy stored in a capacitor be increased indefinitely by increasing voltage?

In theory, yes, but in practice, no. There's a maximum voltage (breakdown voltage) beyond which the dielectric will fail, allowing current to flow between the plates. This limits the maximum energy that can be safely stored in a real capacitor.

23. How is the energy stored in a capacitor related to its charge?

The energy stored in a capacitor is directly proportional to the square of the charge stored on its plates. As more charge is added, the energy increases quadratically, not linearly.

24. What's the formula for calculating the energy stored in a capacitor?

The energy (E) stored in a capacitor can be calculated using three equivalent formulas:

25. Why is there a factor of 1/2 in the capacitor energy formula?

The factor of 1/2 appears because the voltage across the capacitor increases linearly as it charges. The average voltage during charging is half the final voltage, so the energy is half of what it would be if the full voltage were present throughout the charging process.

26. What is the energy stored in a capacitor?

The energy stored in a capacitor is the electrical potential energy stored in the electric field between its plates. This energy is a result of the work done to separate charges against the electric field during the charging process.

27. How does increasing the voltage affect the energy stored in a capacitor?

Increasing the voltage has a quadratic effect on the energy stored. Doubling the voltage will increase the stored energy by a factor of four, as the energy is proportional to V².

28. How does the plate separation affect the energy stored in a parallel plate capacitor?

Increasing the plate separation decreases the capacitance, which, if the charge is held constant, will increase the energy stored. However, if the voltage is held constant, increasing plate separation will decrease the energy stored as it reduces the capacitance.

29. What happens to the energy in a capacitor if you connect two identical charged capacitors in parallel?

When two identical charged capacitors are connected in parallel, charge redistributes until the voltage is the same across both. The total energy of the system decreases, with some energy being lost as heat during the charge redistribution process.

30. Can the energy stored in a capacitor be used to do mechanical work?

Yes, the energy stored in a capacitor can be used to do mechanical work. For example, it can be used to power electric motors in applications where short bursts of high power are needed, such as in camera flashes or defibrillators.

31. What's the relationship between the energy stored in a capacitor and the work done by the electric field?

The energy stored in a capacitor is equal to the work done against the electric field to separate the charges. When the capacitor discharges, this stored energy is released as the electric field does work to move the charges back together.

32. How does the concept of energy stored in a capacitor relate to the conservation of energy?

The energy stored in a capacitor demonstrates the conservation of energy principle. The work done to charge the capacitor is stored as electric potential energy in the field. This energy is not lost but converted to other forms (like heat or mechanical work) when the capacitor is discharged.

33. How does the energy stored in a capacitor compare in series vs. parallel combinations?

For a given total capacitance and applied voltage, capacitors in parallel will store more energy than the same capacitors in series. This is because parallel connection increases total capacitance, while series connection decreases it.

34. What's the significance of the area under a voltage-charge graph for a capacitor?

The area under a voltage-charge graph for a capacitor represents the energy stored in the capacitor. This graphical representation helps visualize why the energy formula contains a factor of 1/2 - it's half the area of the rectangle formed by the final voltage and charge.

35. How does the energy stored in a capacitor relate to its ability to smooth voltage in circuits?

The energy stored in a capacitor allows it to act as a voltage stabilizer in circuits. When voltage drops, the capacitor can release its stored energy to maintain the voltage level. Conversely, when voltage spikes, the capacitor can absorb excess energy, smoothing out fluctuations.

36. What role does the energy stored in capacitors play in renewable energy systems?

In renewable energy systems, capacitors can store energy to help manage the intermittent nature of sources like solar and wind. They can quickly release energy to stabilize power output during short-term fluctuations, complementing batteries which handle longer-term storage.

37. How does the energy stored in a capacitor relate to its discharge time?

The energy stored in a capacitor directly affects its discharge time. A capacitor with more stored energy will take longer to discharge through a given resistance. The discharge follows an exponential decay, with the time constant depending on the capacitance and resistance.

38. Can the energy stored in a capacitor be used to create magnetic fields?

Yes, the energy stored in a capacitor can be used to create magnetic fields. When a capacitor discharges through a coil of wire, it creates a changing electric current, which in turn produces a magnetic field. This principle is used in some electromagnetic pulse generators.

39. How does the energy stored in a capacitor relate to its potential difference?

The energy stored in a capacitor is proportional to the square of the potential difference (voltage) across its plates. This quadratic relationship means that doubling the voltage will quadruple the stored energy, assuming the capacitance remains constant.

40. How does the energy stored in a capacitor relate to electric field energy density?

The energy stored in a capacitor is the integral of the electric field energy density over the volume between the plates. The electric field energy density at any point is given by ½ε₀E², where ε₀ is the permittivity of free space and E is the electric field strength at that point.

41. Can the energy stored in a capacitor be used in quantum computing?

While capacitors themselves are classical components, the energy they store can be used in supporting systems for quantum computers. For example, they can help in providing stable power supplies or in rapidly changing electromagnetic fields used to manipulate qubits.

42. How does the energy stored in a supercapacitor differ from that in a regular capacitor?

Supercapacitors can store much more energy than regular capacitors due to their higher capacitance. This is achieved through the use of porous materials with very high surface areas. The energy storage mechanism also involves some electrochemical processes, not just pure electrostatic storage.

43. What happens to the energy stored in a capacitor if you suddenly change the dielectric material?

If you could instantaneously change the dielectric material, the energy stored would change. Increasing the dielectric constant would decrease the energy if charge is held constant, or increase the energy if voltage is held constant. In practice, such a sudden change is not physically realizable.

44. How does the concept of energy stored in a capacitor relate to the breakdown of dielectrics?

The breakdown of a dielectric occurs when the electric field becomes strong enough to ionize the dielectric material. This is directly related to the energy stored, as the electric field strength increases with stored energy. The maximum energy a capacitor can safely store is limited by its dielectric strength.

45. Can the energy stored in a capacitor be used to explain the concept of voltage?

Yes, the energy stored in a capacitor can help explain voltage. Voltage can be understood as the energy per unit charge stored in the capacitor. Mathematically, V = E/Q, where E is the energy stored and Q is the charge, which is consistent with the capacitor energy formulas.

46. How does the energy stored in a capacitor relate to the concept of electrical potential?

The electrical potential (voltage) between the plates of a capacitor is a measure of the work per unit charge required to move charge between the plates. This work is stored as potential energy in the capacitor. The total energy stored is the product of this potential and the charge, divided by two.

47. What's the relationship between the energy stored in a capacitor and its maximum power output?

The maximum power a capacitor can deliver is related to its stored energy and how quickly it can be discharged. While the stored energy determines the total available energy, the maximum power is limited by factors like internal resistance and the characteristics of the discharge circuit.

48. How does the energy stored in a capacitor relate to the concept of capacitive reactance?

While energy storage is a DC concept, capacitive reactance is an AC concept. However, they're related: capacitive reactance determines how a capacitor responds to AC, affecting how quickly it can charge and discharge, which in turn affects its ability to store and release energy in AC circuits.

49. Can the energy stored in a capacitor be used to explain why capacitors block DC but pass AC?

Yes, the energy storage property of capacitors helps explain this behavior. With DC, once the capacitor is charged to the applied voltage, no more current flows as it's fully "filled" with energy. With AC, the constantly changing voltage causes the capacitor to continuously charge and discharge, effectively passing the AC signal.

50. How does the energy stored in a capacitor relate to its impedance in AC circuits?

The energy storage capability of a capacitor is directly related to its capacitance, which determines its impedance in AC circuits. A higher capacitance means more energy storage capability and lower impedance at a given frequency, allowing more AC current to flow.

51. What's the significance of the time constant in relation to the energy stored in a capacitor?

The time constant (τ = RC) determines how quickly a capacitor can charge or discharge, and thus how quickly it can store or release its energy. It represents the time taken for the capacitor to charge to about 63% of its full energy storage capacity, or to discharge to about 37% of its initial energy.

52. How does the energy stored in a capacitor relate to the concept of displacement current?

The changing electric field as a capacitor charges or discharges gives rise to the displacement current. This current is directly related to the rate of change of the energy stored in the capacitor's electric field, as described by Maxwell's extension to Ampère's law.

53. Can the energy stored in a capacitor be used to explain the behavior of dielectrics in electric fields?

Yes, the energy storage in capacitors helps explain dielectric behavior. Dielectrics increase a capacitor's energy storage capacity by becoming polarized in the electric field. This polarization reduces the field inside the dielectric, allowing more charge to be stored on the plates for a given voltage.

54. How does the energy stored in a capacitor relate to its self-resonant frequency?

While not directly related, both energy storage and self-resonant frequency are affected by a capacitor's physical characteristics. The self-resonant frequency is the frequency at which the capacitor's reactance is canceled by its inherent inductance. This limits the frequencies at which the capacitor can effectively store and release energy.

55. What's the relationship between the energy stored in a capacitor and its equivalent series resistance (ESR)?

The ESR doesn't directly affect the energy storage capacity, but it does affect how quickly and efficiently the capacitor can charge and discharge. A higher ESR results in more energy being lost as heat during charge/discharge cycles, reducing the effective energy available from the capacitor.

56. How does the concept of energy stored in a capacitor relate to the piezoelectric effect?

The piezoelectric effect, where mechanical stress produces an electric charge in certain materials, can be thought of as converting mechanical energy into electrical energy stored in the material (which acts like a capacitor). Conversely, applying a voltage (adding electrical energy) to a piezoelectric material causes mechanical deformation.

57. Can the energy stored in a capacitor be used to explain the concept of electric field lines?

Yes, the energy stored in a capacitor is directly related to the electric field between its plates. Electric field lines provide a visual representation of this field. The density of these lines represents the field strength, which is directly related to the energy density of the electric field and thus to the total energy stored in the capacitor.