Energy stored in an inductor

Inductors, fundamental components in electrical circuits, possess the remarkable ability to store energy in the form of a magnetic field when an electric current flows through them. This energy storage capability is crucial in various applications, from power supplies to radio transmitters. In real life, inductors are akin to the way a water reservoir stores potential energy by holding water at a height, ready to release it when needed. Similarly, an inductor stores electrical energy and releases it when required, ensuring smooth and efficient operation of electrical systems. This principle finds practical use in devices such as transformers, which transfer energy between circuits, and in electrical grids, where inductors help manage the flow of electricity, maintaining stability and preventing surges. In this article we will understand the energy stored in an inductor not only deepens our grasp of electrical engineering but also highlights the seamless integration of these components into our daily lives, powering a range of modern technologies.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Energy Stored in an Inductor
2. Solved Examples Based on Energy Stored In An Inductor
3. Summary

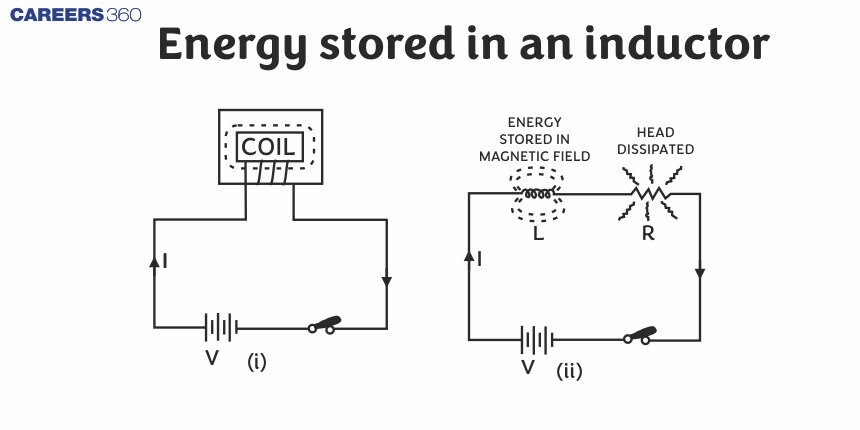
Energy Stored in an Inductor

Inductors, fundamental components in electrical circuits, possess the remarkable ability to store energy in the form of a magnetic field when an electric current flows through them. This energy storage capability is crucial in various applications, from power supplies to radio transmitters. In real life, inductors are akin to the way a water reservoir stores potential energy by holding water at a height, ready to release it when needed. In building a steady current in the circuit, the source emf has to do work against of self-inductance of the coil and whatever energy is consumed for this work is stored in the magnetic field of the coil this energy is called as magnetic potential energy (U) of the coil. When an electric current i is flowing in an inductor, there is energy stored in the magnetic field. Considering a pure inductor L, the instantaneous power which must be supplied to initiate the current in the inductor is

$P=i v=L i \frac{d i}{d t}$

The work done by the voltage source during a time interval $d t$ is

$d W=P d t=i L \frac{d i}{d t} d t=L i d i$

total work $W$ done in establishing the final current $I$ in the inductor

$\mathrm{W}=\int_0^t P d t=\int_0^I L i d i=\frac{1}{2} L I^2$

So Energy stored in the magnetic field of the inductor is given as

$U=\frac{1}{2} L I^2$

The energy density (u)/Energy per unit volume using $U=\frac{1}{2} L I^2$

for the solenoid field, we can write

$\begin{aligned} & U=\frac{1}{2}(L i) i=\frac{N \phi i}{2} \\ & u=\frac{U}{V}=\frac{B^2}{2 \mu_0}\end{aligned}$

Recommended Topic Video

Solved Examples Based on Energy Stored In An Inductor

Example 1: The Self-induced emf of a coil is 25 volts, When the current in it is changed at a uniform rate from 10 A to 25 A in 1s, the change in the energy (in J) of the inductance is

1) 437.5

2) 740

3) 637.5

4) 540

Solution:

Faraday's Second Law of Induction emf

$\varepsilon=\frac{-d \phi}{d t}=-L \frac{d I}{d t}$

Energy stored in the magnetic field of the inductor

$\begin{aligned} & U=\frac{1}{2} L I^2 \\ & L \frac{d i}{d t}=25 \\ & L=\frac{25 \times 1}{15}=\frac{5}{3} \\ & \Delta E=\frac{1}{2} \times \frac{5}{3}\left(25^2-10^2\right)=437.5\end{aligned}$

Hence, the answer is the Option (1).

Example 2: The dimension of quantity $\frac{1}{2} \frac{B^2}{\mu_0}$

1) $M L^2 T^{-2} A^{-2}$
2) $M L^2 T^{-2} A^{-1}$
3) $M L^2 T^{-2} A$
4) $M L^{-1} T^{-2}$

Solution:

Energy Density( u)

$u=\frac{U}{V}=\frac{B^2}{2 \mu_0}$

wherein

$\frac{U}{V}=$ Energy stored per unit volume

Energy density $=\frac{1}{2} \frac{B^2}{\mu_0}$

Energy density $=\frac{\text { Energy }}{\text { volume }}$

$=\frac{M L^2 T^{-2}}{L^3}$

Dimension $=M L^{-1} T^{-2}$

Hence, the answer is the option (4).

Example 3: A coil of inductance 2H having negligible resistance is connected to a source of supply whose voltage is given by V=3t volt. (where t is second). If the voltage is applied when t=0, then the energy stored in the coil after 4s is _______.

1) 144

2) 146

3) 148

4) 150

Solution:

$\begin{aligned} & \mathrm{L} \frac{\mathrm{di}}{\mathrm{dt}}=\varepsilon=3 \mathrm{t} \\ & \mathrm{L} \int \mathrm{di}=3 \int t \mathrm{dt} \\ & \mathrm{Li}=\frac{3 \mathrm{t}^2}{2} \\ & \mathrm{i}=\frac{3 \mathrm{t}^2}{2 \mathrm{~L}} \\ & \text { for } \mathrm{t}=4 \text { sec } \\ & \mathrm{i}=12 \mathrm{~A} \\ & \text { Energy }=\mathrm{U}=\frac{1}{2} \mathrm{LI}^2=\frac{1}{2} \times 2(12)^2=144 \mathrm{~J}\end{aligned}$

Hence, the answer is (144)

Example 4: The time taken for the magnetic energy to reach 25% of its maximum value where a solenoid of resistance R, inductance L is connected to a battery, is:

1) $\frac{L}{R} \ln 2$
2) infinite
3) $\frac{L}{R} \ln 5$
4) $\frac{L}{R} \ln 10$

Solution:

Magnetic energy $=\frac{1}{2} L I^2$

If the Magnetic energy is 25% of the maximum value having the same value of L then the value of the current must be half of the maximum value of the current.
So, $I=\frac{I_o}{2}$

Where, $I_0$ is the maximum current flow through the L-R circuit

From current-time relations, we know that,

$\begin{aligned} & I=I_0\left(1-e^{-R t / L}\right) \\ & \frac{I_o}{2}=I_0\left(1-e^{-R t / L}\right)\end{aligned}$

Solving it,
We will get

$t=\frac{L}{R} \ln 2$

Hence, the answer is the option(1).

Example 5: What is the time at which the rate of dissipation of energy (Joule's heat) across the resistance is equal to the rate at which magnetic energy is stored in the inductor?

1) 1.4 sec

2) 1.9 sec

3) 5 sec

4) 0.03 sec

Solution:

Charging of Inductor

$\begin{aligned} & i=i_0\left(1-e^{-\frac{t}{\tau}}\right) \\ \tau= & \frac{L}{R} \\ & i_0=\text { max current } \\ \tau= & \text { Time constant }\end{aligned}$

For L-R circuit

$i=\frac{E}{R}\left(1-e^{-t / \tau}\right)_{\text {where }} \tau=\frac{L}{R}$

and rate of magnetic energy stored in the inductor $=i \times L \times \frac{d i}{d t} \ldots \ldots(1)$

and rate of dissipation of energy across Resistance $=i^2 R \quad \ldots \ldots(2)$

from question

$\begin{aligned} & \mathrm{So}^{i^2 R}=i L \frac{d i}{d t} \\ & R \times \frac{E}{R}\left(1-e^{-\frac{R t}{L}}\right)=\left(L \times \frac{E}{R} \times \frac{R}{L} e^{-\frac{R t}{L}}\right) \\ & \Rightarrow 2 e^{-\frac{R t}{L}}=1 \\ & \frac{R}{L} t=\ln 2 \\ & t=\frac{L}{R} \ln 2 \\ & t=2 \ln 2 \\ & \mathrm{t}=1.4 \mathrm{sec}\end{aligned}$

Hence, the answer is the option(1).

Summary

Inductors store energy in the form of a magnetic field, crucial for smooth operation in electrical circuits and devices like transformers and power supplies. The energy stored can be calculated using $U=\frac{1}{2} L I^2$ . This principle is essential for managing electrical energy flow, ensuring stability, and preventing surges in various applications, from household appliances to industrial power systems. Practical examples illustrate how inductors help maintain energy efficiency and system reliability in real-world scenarios.