Epsilon Naught Value - Meaning, Unit, Formula, FAQs
Epsilon Naught $\left(\varepsilon_0\right)$, or permittivity of free space, is the base physical constant explaining how electric fields are related in a vacuum. Its value is, indeed very important to understanding electromagnetic waves, Coulomb's law and capacitance. It is given in farads per meter $(F/m)$ units and is crucial in calculating electric forces strength behaviour and material inside an electric field. Its importance can be realized in real life from the design of capacitors, communication system functions, and even in the midst of nature, such as lightning.
This Story also Contains
- What is Epsilon Naught?
- Uses of Epsilon Naught $\left(\boldsymbol{\varepsilon}_{\mathbf{0}}\right)$
- Example Problem: Using Epsilon Naught $\left(\varepsilon_0\right)$ in Calculation
What is Epsilon Naught?
Epsilon naught, written as $\boldsymbol{\varepsilon}_{\mathbf{0}}$, is called the permittivity of free space (vacuum). It is a constant that shows how much electric field can pass through empty space. In simple words, it tells us how strongly charges interact in a vacuum.
Epsilon Naught: What Does it Mean?
Free space permittivity is an epsilon value that is nought in physics. The amount of electric field that can penetrate into free space or a vacuum (actually, it is a mathematical quantity).
This physical constant represents the absolute dielectric permittivity of a vacuum and is also known as the permittivity of free space. The epsilon value naught quantity represents the ability of a vacuum to permit the flow of electric field lines.
- The dielectric permittivity of free space is represented by this number.
- An element's dielectric constant is calculated using Epsilon naught.
- A brief overview of Epsilon naught and its equivalent in SI is provided, along with details on its importance and practical applications.
What is the Value of Epsilon Naught $\left(\epsilon_0\right)$?
In SI Units:
A unit of measurement equal to $8.854187817 \times 10^{-12} \mathrm{~F}^{-1} \mathrm{~m}^{-1}$ (SI Unit). Where F is Farad
In CGS Unit
$
\epsilon_0=1
$
Units of Epsilon Naught
It is possible to express the permittivity of free space $\left(\epsilon_0\right)$ in SI units as well as CGS units. The Epsilon unit is briefed as follows:
|
Epsilon naught Units
|
Units
|
|
Epsilon nought in SI
| Farad per meter or F.m-1 |
Uses of Epsilon Naught $\left(\boldsymbol{\varepsilon}_{\mathbf{0}}\right)$
Epsilon naught, or the permittivity of free space, is a fundamental constant in physics with several important uses:
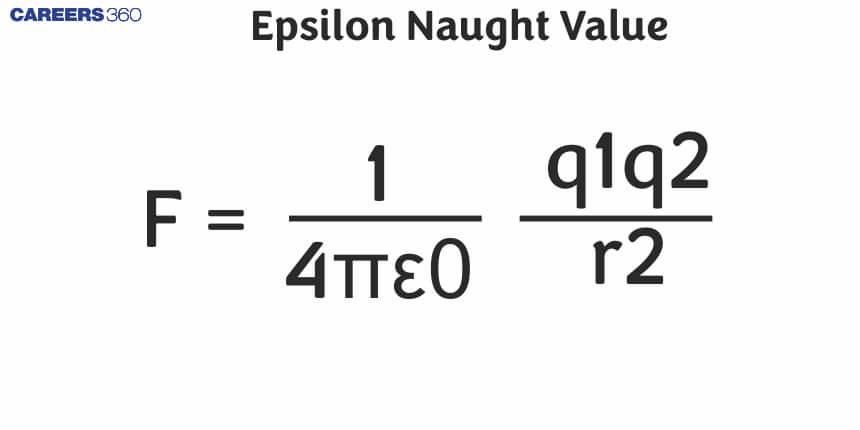
1. Coulomb's Law: It helps calculate the force between two point charges in a vacuum.
$
F=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_1 q_2}{r^2}
$
2. Gauss's Law: Appears in the formula relating electric flux through a closed surface to the enclosed charge.
3. Capacitance Calculations: Determines the capacitance of capacitors in vacuum or air.
$
C=\varepsilon_0 \frac{A}{d}
$
4. Electrostatics Formulas: Used in electric field, potential, and energy calculations for charges in free space.
Example Problem: Using Epsilon Naught $\left(\varepsilon_0\right)$ in Calculation
Problem: Two charges $q_1=2 \mu C$ and $q_2=3 \mu C$ are 0.5 m apart in vacuum. Find the force.
Solution:
$$
\begin{gathered}
F=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}, \quad \frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \\
F=9 \times 10^9 \cdot \frac{\left(2 \times 10^{-6}\right)\left(3 \times 10^{-6}\right)}{0.5^2}=0.216 \mathrm{~N}
\end{gathered}
$$
Answer: $F=0.216 \mathrm{~N}$
NCERT Physics Notes:
Frequently Asked Questions (FAQs)
It helps determine the strength of electric forces in vacuum, calculate electric fields, and is essential in formulas involving capacitance and electrostatic energy.
Epsilon naught is used in Coulomb’s law, Gauss’s law, capacitance calculations, and in many electrostatics formulas to relate electric charges and fields.
Yes, in the SI system, epsilon naught has the unit C²/N·m², while in CGS units it is unitless.
The SI unit of epsilon naught is Coulomb squared per Newton meter squared (C²/N·m²). In CGS units, it is considered dimensionless.
The permittivity of free space (ϵ0) can be characterized as the capacity of the classical vacuum to allow electric fields. The Epsilon naught formula is associated with 8.854187817 x 10-12 F.m-1
Previously we discussed the permittivity of space, which is a constant in numerical problems.
With the help of Coulomb's law, it determines the force between two charged particles.
The capacitance of an insulator can be determined with it.
A permittivity ratio is a measure of free space's permittivity in physics. In addition, this quantity describes the extent of an electric field that can exist in a vacuum or free space.