First Law Of Thermodynamics

The First Law of Thermodynamics is a basic principle that tells us energy cannot be created or destroyed, only transformed from one form to another. This law helps us understand everything from how we generate electricity to how our bodies use food for energy. For students preparing for board exams and competitive exams like JEE and NEET, mastering this concept is key. This article breaks down the First Law of Thermodynamics into easy-to-understand terms and includes a solved example to demonstrate how this law applies in practical scenarios, ensuring you can see the direct application of what you're learning.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. The First law of Thermodynamics
2. Solved Examples Based on the First Law of Thermodynamics
3. Summary

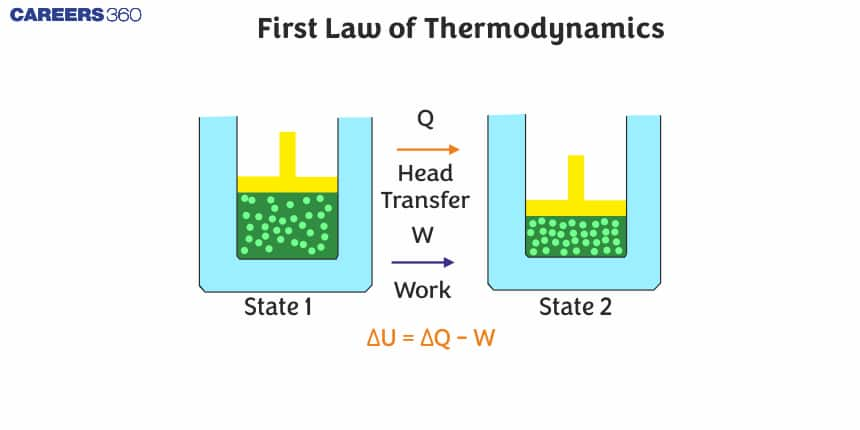
The First law of Thermodynamics

According to it, heat given to a system (Q) is equal to the sum of an increase in its internal energy (U) and the work done (W) by the system against the surroundings.

$\Delta Q=\Delta U+\Delta W$

or For cyclic process

$\sum \Delta Q=\sum \Delta W$

Drawback of the First law of Thermodynamics

The first law of thermodynamics does not tell us the reason for the direction of heat transfer.

Important points

1. Q and W are the path functions but U is the point function.

2. The first law of thermodynamics introduces the concept of internal energy.

Recommended topic video on ( First law of Thermodynamics)

Solved Examples Based on the First Law of Thermodynamics

Example 1: Which of the following is incorrect regarding the first law of thermodynamics?

1) It introduces the concept of the internal energy

2) It introduces the concept of entropy

3) It is applicable to any cyclic process

4) It is a restatement of the principle of conservation of energy

Solution:

The first law of Thermodynamics

Heat imported to a body is in general used to increase internal energy and work done against external pressure.

wherein

$d Q=d U+d W$

Entropy

It is a measure of the disorder of molecular motion of a system.

wherein

Greater is disorder greater is entropy

$d S=\frac{d Q}{T}$

The concept of entropy is introduced in the second law of thermodynamics.

The first law dealt with internal energy, work, and heat energy.

It is a statement of the first law of thermodynamics.

Hence, the answer is the option (2).

Example 2: A gas is compressed from a volume of 2 m³ to a volume of 1 m³ at a constant pressure of 100 N/m². Then it is heated at constant volume by supplying 150 J. of energy. As a result, the internal energy of the gas: 1) Increases by 250 J

2) Decreases by 250 J

3) Increases by 50 J

4) Decreases by 50 J

Solution:

The first law of Thermodynamics

Heat imported to a body is in general used to increase internal energy and work done against external pressure.

wherein

$
\begin{aligned}
& d Q=d U+d W \\
& \quad \Delta U=\Delta Q-W \\
& \Delta Q=150 J \\
& W=P \Delta V=100 \mathrm{~N} / \mathrm{m}^2\left(1 \mathrm{~m}^3-2 \mathrm{~m}^3\right)=-100 \mathrm{~J} \\
& \Delta U=150 \mathrm{~J}-(-100 \mathrm{~J})=250 \mathrm{~J}
\end{aligned}
$

U is increased by 250 J

Hence, the answer is the option (1).

Example 3: A gas can be taken from A to B via two different processes ACB and ADB.

When path ACB is used 60 J of heat flows into the system and 30 J of work is done by the system. If path ADB is used work done by the system is 10 J. The heat Flow (in J) into the system in path ADB is :

1) 40

2) 80

3) 100

4) 20

Solution:

The first law of Thermodynamics

Heat imported to a body is in general used to increase internal energy and work done against external pressure.

wherein

$
d Q=d U+d W
$

For ACB
$
\begin{aligned}
& \Delta Q_{A C B}=\Delta W_{A C B}+\Delta U_{A C B} \\
& 60 \mathrm{~J}=30 \mathrm{~J}+\Delta U_{A C B} \\
& \Rightarrow \Delta U_{A C B}=30 \mathrm{~J} \\
& \Delta U_{A C D}=\Delta U_{A C B}=30 \mathrm{~J}
\end{aligned}
$

For ACD
$
\Delta Q_{A C D}=\Delta U_{A C B}+\Delta W_{A D B}
$

= 30 + 10 = 40 J

Example 4: When heat $Q$ is supplied to a diatomic gas of rigid molecules, at constant volume its temperature increases by $\Delta T$. The heat required to produce the same change in temperature, at constant pressure is :

1) $\frac{2}{3} Q$
2) $\frac{5}{3} Q$
3) $\frac{7}{5} Q$
4) $\frac{3}{2} Q$

Solution:

$
\begin{aligned}
& Q=n C_v \Delta T \\
& Q^{\prime}=n C_p \Delta T \\
& \therefore \frac{Q^{\prime}}{Q}=\frac{C_p}{C_v}
\end{aligned}
$

For diatomic gas : $\frac{C_p}{C_v}=\gamma=\frac{7}{5}$
$
Q^{\prime}=\frac{7}{5} Q
$

Hence, the answer is the option (3).

Example 5: The following figure shows two processes $A$ and $B$ for a gas. If $\Delta Q_A$ and $\overline{\Delta Q_B}$ are the amount of heat absorbed by the system in two cases, and $\Delta U_A$ and $\Delta U_B$ are changes in internal energies, respectively, then:

1) $\Delta Q_A<\Delta Q_B, \Delta U_A<\Delta U_B$
2) $\Delta Q_A>\Delta Q_B, \Delta U_A>\Delta U_B$
3) $\Delta Q_A>\Delta Q_B, \Delta U_A=\Delta U_B$
4) $\Delta Q_A=\Delta Q_B, \Delta U_A=\Delta U_B$

Solution:

Internal energy is a state function

So, $\Delta U_A=\Delta U_B$
Now, $\Delta Q=\Delta U+W$
Now $W_A>W_B$ (work is Area under the curve)
So, $\Delta Q_A>\Delta Q_B$.

Summary

The law of energy conservation (the first law of thermodynamics) says that energy can be neither created nor destroyed, only transferred or transformed. With any happening, the product of an entire isolated system is constant. Certain addition of a high-temperature substance to a certain quantity of material might increase its heating.