Hysteresis Curve: Definition, Diagram and Meaning

Hysteresis Curve

Edited By Vishal kumar | Updated on Jul 02, 2025 08:05 PM IST

The hysteresis curve, also known as the B-H curve, represents the relationship between magnetic flux density (B) and magnetic field strength (H) in a ferromagnetic material. When a magnetic field is applied to such materials, they exhibit a lagging response in magnetization, creating a looped curve when plotted. This phenomenon, called hysteresis, shows how the material retains some magnetism even after the external magnetic field is removed.

This Story also Contains

Hysteresis
Solved Examples Based on Hysteresis curve
Summary

In real life, hysteresis can be observed in everyday objects like fridge magnets or electromagnets. For example, when you turn off an electromagnet, it doesn't immediately lose its magnetism, illustrating the concept of magnetic memory. Similarly, in mechanical systems like car suspensions, materials can exhibit hysteresis, as they take time to return to their original state after being stressed. Understanding the hysteresis curve is essential in designing efficient transformers, motors, and memory storage devices.

Hysteresis

It is the property of the Lagging of magnetic induction (B) behind magnetic intensity (H) in the case of the ferromagnetic substances.

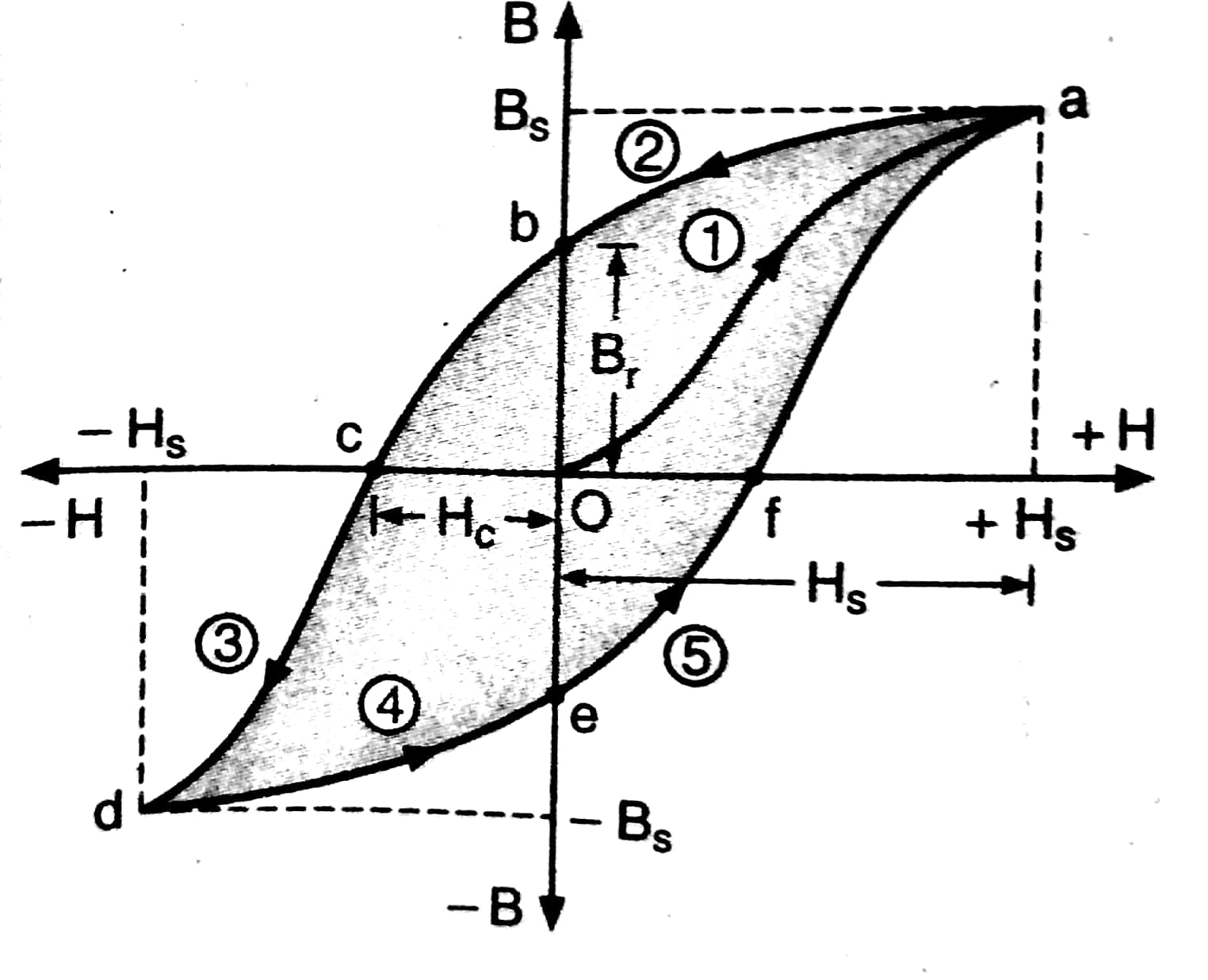
Hysteresis Curve- This is nothing but the graph of (B Vs H )or (I Vs H) as shown below.

When a non-magnetized material is placed in the long solenoid which is carrying current i as shown in the below figure.

Initially When $i=0$ then $B=0, H=0, I=0$ l.e at Point O .
Now if we increase i, it will result in an increase in B and H and 1 , till saturation point (a) I.e path 1 or Path Oa
Now we decrease H and reduce it to zero by decreasing $\mathrm{i} \Rightarrow \mathrm{I}$.e path 2 or Path ab .
So at point $\mathrm{b}, \mathrm{H}=0$ but $B \neq 0 \Rightarrow B=B_r$ where $\mathrm{B}_{\mathrm{r}}$ is called retentivity or remanence or residual magnetism.
This is happening because, For ferromagnetic materials, by removing the external magnetic field, i.e. $\mathrm{H}=0$, the magnetic moment of some domains remains aligned in the applied direction of the previous magnetising field, resulting in a residual magnetism.

Now we have to remove this residual magnetism of the material or demagnetize the material completely. For this, we will reverse the direction of the current in the solenoid.
So, the process of demagnetizing a material completely (i.e path bc) by applying the magnetizing field in a negative direction is defined as Coercivity.
So At point $c$ we have $B=0$ and $H=H_c$ where $H_c$ is called coercivity.

Coercivity signifies magnetic hardness or softness of substance:
I.,e Magnetic hard substance (steel) ——> High coercivity
Magnetic soft substance (soft iron) ——> Low coercivity.

If, after the magnetization has been reduced to zero, the value of H is further increased in the 'negative' i.e. reversed direction, the material again reaches a state of magnetic saturation, represented by point d.

Next, the current is reduced (curve de) and reversed (curve ea) then The cycle repeats itself till point a.

Solved Examples Based on Hysteresis curve

Example 1: The use of the study of hysteresis curve for a given material is to estimate the

1) Voltage Loss

2) Hysteresis loss

3) Current loss

4) All of the these

Solution:

Hysteresis

Lagging of magnetic induction (B) behind magnetic intensity (H)

Hysteresis loss is given by the hysteresis curve between I & H

Hence, the answer is the option(2).

Example 2: The B-H curve for a ferromagnet is shown in the figure. The ferromagnet is placed inside a long solenoid with 1000 turns/cm. The current (in mA) that should be passed in the solenoid to demagnetise the ferromagnet completely is :

1) 1

2) 2

3) 20

4) 40

Solution:

Hysteresis Curve

The graph between B and H is called hysteresis curve

wherein

Magnetic field intensity inside the material will be given by H=ni
and for demagnetization, H=100

so required current

$i=\frac{100}{1000 \text { turns } / \mathrm{cm}}=\frac{100}{10^5 \text { turns } / \mathrm{m}}=1 \mathrm{~mA}$

Hence, the answer is the option(1).

Example 3: The materials suitable for making electromagnets should have

1) high retentivity and high coercivity

2) low retentivity and low coercivity

3) high retentivity and low coercivity

4) low retentivity and high coercivity.

Solution:

Coercivity $(H)$
When $H=H_c, B=0$
i.e. Magnetising fields $(\mathrm{H})$ required to destroy the residual magnetism.

Retentivity -
When $\mathrm{H}=0$ (after having increased from 0 to $\mathrm{H}_{\mathrm{s}}$ ), $\mathrm{B}=\mathrm{B}_{\mathrm{r}}$
$B_r$ - residual magnetism, retentivity

The coercivity of a ferromagnetic material is the intensity of the applied magnetic field required to reduce the magnetization of that material to zero after the magnetization of the sample has been driven to saturation.

Materials of high retentivity and low coercivity are suitable for making electromagnets.

Hence the answer is option (2).

Example 4: Hysteresis loops for two magnetic materials A and B are given below :

These materials are used to make magnets for electric generators, transformer core and electromagnet core. Then it is proper to use :

1) A for electric generators and transformers.

2) A for electromagnets and B for electric generators.

3) A for transformers and B for electric generators.

4) B for electromagnets and transformers.

Solution:

Retentivity
When $\mathrm{H}=0$ (after having increases from 0 to $\mathrm{H}_s$ ), $B=B_r$
$B_r$ - residual magnetism, retentivity
Coercivity $(H)$ -
When $H=H_c, B=0$
wherein
i.e Magnetising fields $(\mathrm{H})$ required to destroy the residual magnetism.

Material with higher value of refentivity and coerceivity is good to make permenent magnets i.e A
Graph B is for making electro-magnets and transformers.

Hence the answer is option (4).

Example 5:

The figure gives experimentally measured B vs. H variation in a ferromagnetic material. The retentivity, co-ercivity and saturation, respectively, of the material are :

1) $1.5 \mathrm{~T}, 50 \mathrm{~A} / \mathrm{m}$ and 1.0 T
2) $1.0 \mathrm{~T}, 50 \mathrm{~A} / \mathrm{m}$ and 1.5 T
3) $1.5 \mathrm{~T}, 50 \mathrm{~A} / \mathrm{m}$ and 1.0 T
4) $150 \mathrm{~A} / \mathrm{m}, 1.0 \mathrm{~T}$ and 1.5 T

Solution:

So, from the figure, we can see that the-

x = retentivity, y = coercivity, z = saturation magnetization

So, by matching with the diagram from the question and solution, option (2) is correct.

Summary

The hysteresis curve illustrates the relationship between magnetic flux density (B) and magnetic field strength (H) in ferromagnetic materials. It shows how these materials retain magnetism even after the external magnetic field is removed, demonstrating properties like retentivity (residual magnetism) and coercivity (the field needed to demagnetize). This curve is critical for understanding energy losses, hysteresis losses, and designing electromagnets, transformers, and permanent magnets with appropriate materials based on their magnetic properties.

Frequently Asked Questions (FAQs)

1. What is a hysteresis curve in magnetism?

A hysteresis curve is a graphical representation of the relationship between the magnetic field strength (H) and the magnetic flux density (B) in a ferromagnetic material as it undergoes magnetization and demagnetization. It shows how the material's magnetization changes as the external magnetic field is varied, revealing important properties like remanence and coercivity.

2. Why does the hysteresis curve form a loop instead of a single line?

The hysteresis curve forms a loop because ferromagnetic materials exhibit a "memory" effect. As the external magnetic field is increased and then decreased, the material's magnetization doesn't follow the same path. This lag or delay in response creates the characteristic loop shape, which represents energy dissipation in the material during the magnetization cycle.

3. What does the area inside the hysteresis loop represent?

The area inside the hysteresis loop represents the energy lost per unit volume of the material during one complete magnetization cycle. This energy is dissipated as heat in the material, a phenomenon known as hysteresis loss. Materials with larger loop areas have higher energy losses and are typically used in applications where heat generation is desired, such as induction heating.

4. How does the shape of the hysteresis curve relate to a material's magnetic properties?

The shape of the hysteresis curve provides information about a material's magnetic properties. A narrow, tall loop indicates a magnetically "hard" material suitable for permanent magnets, while a wide, short loop suggests a magnetically "soft" material ideal for transformers and electromagnets. The curve's shape also reveals properties like saturation magnetization, remanence, and coercivity.

5. What is magnetic saturation, and how is it represented on the hysteresis curve?

Magnetic saturation is the state reached when an increase in the applied external magnetic field can't cause a further increase in the material's magnetization. On the hysteresis curve, it's represented by the flattening of the curve at high field strengths, forming the upper and lower extremities of the loop where the curve becomes nearly horizontal.

6. How does the concept of magnetic susceptibility relate to the hysteresis curve?

Magnetic susceptibility is a measure of how much a material will become magnetized in an applied magnetic field. It's related to the slope of the magnetization curve (M vs. H) rather than the B vs. H curve of the typical hysteresis loop. However, for materials with low permeability, the two curves are similar. The susceptibility can be thought of as the "ease of magnetization" and is particularly important in the initial part of the curve. Materials with high susceptibility show a rapid increase in magnetization with applied field.

7. How does temperature affect the hysteresis curve?

Temperature significantly influences the hysteresis curve. As temperature increases, the curve generally becomes narrower and shorter. This is because thermal energy makes it easier for magnetic domains to align and realign, reducing coercivity and remanence. At the Curie temperature, ferromagnetic materials become paramagnetic, and the hysteresis effect disappears.

8. What is remanence, and how is it identified on the hysteresis curve?

Remanence, or remanent magnetization, is the magnetic flux density that remains in a material after the external magnetic field is removed. On the hysteresis curve, it's identified as the y-axis intercept (B-axis) when the applied field (H) is zero. It represents the material's ability to retain magnetization in the absence of an external field.

9. How is coercivity related to the hysteresis curve?

Coercivity is the intensity of the applied magnetic field required to reduce the magnetic flux density to zero after the material has been magnetized to saturation. On the hysteresis curve, it's represented by the x-axis intercept (H-axis) when the magnetic flux density (B) is zero. It indicates the material's resistance to demagnetization.

10. Why are some materials said to have "wide" hysteresis loops while others have "narrow" loops?

The width of a hysteresis loop is determined by the material's coercivity. Materials with high coercivity, like hard ferromagnets used in permanent magnets, have wide loops because they require a strong reverse field to demagnetize. Soft ferromagnetic materials, used in transformers, have narrow loops due to their low coercivity, allowing easy magnetization and demagnetization with minimal energy loss.

11. How does the hysteresis curve help in choosing materials for specific applications?

The hysteresis curve provides crucial information about a material's magnetic behavior, helping engineers select appropriate materials for different applications. For instance, materials with narrow loops (low hysteresis loss) are ideal for transformers and motors, while those with wide loops are suitable for permanent magnets. The curve also helps in estimating energy losses and predicting a material's performance under varying magnetic fields.

12. What is the significance of the initial magnetization curve in a hysteresis loop?

The initial magnetization curve, also called the virgin curve, represents the material's first magnetization from a completely demagnetized state. It starts at the origin and rises to meet the main loop. This curve is important because it shows how easily the material can be magnetized from scratch and provides information about the material's magnetic permeability and domain wall movement.

13. How does the frequency of the applied magnetic field affect the hysteresis curve?

As the frequency of the applied magnetic field increases, the hysteresis loop typically becomes wider. This is because at higher frequencies, magnetic domains have less time to align with the changing field, leading to increased energy loss per cycle. This frequency dependence is crucial in applications like transformer core design, where minimizing losses at operating frequencies is essential.

14. What is magnetic retentivity, and how does it differ from remanence?

Magnetic retentivity and remanence are often used interchangeably, but there's a subtle difference. Retentivity is the maximum residual magnetic flux density that a material can retain after saturation, while remanence is the actual residual magnetization when the applied field is reduced to zero. In practice, remanence is often slightly less than retentivity due to self-demagnetization effects.

15. How does the concept of magnetic domains relate to the hysteresis curve?

Magnetic domains are regions within a ferromagnetic material where magnetic moments are aligned. The hysteresis curve reflects the behavior of these domains. As the external field increases, domains aligned with the field grow at the expense of others. The non-linear nature of the curve and the hysteresis effect arise from the energy required to move domain walls and overcome pinning sites within the material.

16. Why is the hysteresis curve important in the design of electrical machines?

The hysteresis curve is crucial in electrical machine design because it helps predict and minimize energy losses. In motors and generators, the core material undergoes repeated magnetization cycles, and the area of the hysteresis loop represents energy lost as heat in each cycle. Designers use this information to select materials and optimize designs to reduce these losses, improving efficiency and preventing overheating.

17. How does grain size in a material affect its hysteresis curve?

Grain size significantly influences a material's hysteresis curve. Generally, materials with larger grain sizes tend to have narrower hysteresis loops, lower coercivity, and lower hysteresis losses. This is because larger grains have fewer grain boundaries, which can act as pinning sites for domain walls. However, very large grains can lead to increased eddy current losses, so an optimal grain size is often sought in practical applications.

18. What is anhysteretic magnetization, and how does it relate to the hysteresis curve?

Anhysteretic magnetization represents the ideal magnetization state of a material without hysteresis effects. It's a theoretical curve that would be followed if the material could reach its lowest energy state at each applied field strength. The anhysteretic curve passes through the center of the hysteresis loop and is useful for understanding the material's intrinsic magnetic properties without the complications of domain wall pinning and other hysteresis-related phenomena.

19. How do impurities and defects in a material affect its hysteresis curve?

Impurities and defects in a material can significantly alter its hysteresis curve. They often act as pinning sites for magnetic domain walls, making it harder for domains to align with the applied field. This typically results in a wider hysteresis loop, increased coercivity, and higher energy losses. However, in some cases, carefully controlled impurities can be used to engineer desired magnetic properties.

20. What is the difference between major and minor hysteresis loops?

A major hysteresis loop is formed when the material is cycled between its positive and negative saturation points. Minor loops, on the other hand, are formed when the material is cycled between intermediate magnetization states without reaching saturation. Minor loops are nested within the major loop and are important in applications where the material operates under partial magnetization conditions, such as in certain types of sensors or memory devices.

21. How does mechanical stress affect a material's hysteresis curve?

Mechanical stress can significantly alter a material's hysteresis curve through a phenomenon called the magnetoelastic effect. Applied stress can change the material's magnetic anisotropy, affecting domain wall movement. Depending on the material and the type of stress (tensile or compressive), the hysteresis loop may become wider or narrower. This relationship is exploited in magnetostrictive materials and stress sensors.

22. What is magnetic viscosity, and how does it relate to the hysteresis curve?

Magnetic viscosity, also known as magnetic after-effect or magnetic relaxation, refers to the time-dependent changes in magnetization after a change in the applied field. It causes a slight "creep" in magnetization over time, even when the external field is constant. This effect can cause slight variations in the hysteresis curve depending on the rate at which the field is changed, particularly affecting the coercivity and remanence measurements.

23. How does the hysteresis curve of a superparamagnetic material differ from that of a ferromagnetic material?

Superparamagnetic materials, typically consisting of very small ferromagnetic particles, exhibit a unique hysteresis behavior. Unlike typical ferromagnetic materials, they show no hysteresis at room temperature when measured over typical laboratory timescales. Their magnetization curve is reversible and S-shaped, without remanence or coercivity. This is because thermal energy can easily flip the magnetic moments of the small particles, resulting in zero net magnetization in the absence of an external field.

24. What is the Barkhausen effect, and how is it related to the hysteresis curve?

The Barkhausen effect is the name given to the noise in the magnetic output of a ferromagnetic material as the applied magnetic field is changed. It's caused by sudden, discontinuous changes in the size and orientation of magnetic domains. On a microscopic level, these jumps contribute to the smoothness of the hysteresis curve. The Barkhausen effect provides insights into the domain structure and can be used to study material properties and detect flaws in magnetic materials.

25. How does the hysteresis curve change as a material approaches its Curie temperature?

As a ferromagnetic material approaches its Curie temperature, its hysteresis curve undergoes significant changes. The loop becomes progressively narrower and shorter, with decreasing remanence and coercivity. This is because thermal energy increasingly disrupts the alignment of magnetic moments. At the Curie temperature, the material transitions to a paramagnetic state, and the hysteresis loop collapses into a single line passing through the origin, as the material no longer retains any permanent magnetization.

26. What is the relationship between a material's crystal structure and its hysteresis curve?

A material's crystal structure strongly influences its hysteresis curve. The crystal structure determines the material's magnetic anisotropy – the preferential directions for magnetization. Materials with high anisotropy, like hexagonal cobalt, tend to have wider hysteresis loops and higher coercivity. Cubic structures, like iron, often have narrower loops. The ease of domain wall movement through the crystal lattice also affects the shape of the curve, with more complex structures generally leading to wider loops due to increased domain wall pinning.

27. How does the concept of exchange bias relate to the hysteresis curve?

Exchange bias is a phenomenon observed in systems with interfaces between ferromagnetic and antiferromagnetic materials. It causes a shift in the hysteresis loop along the field axis, effectively increasing the coercivity in one direction while decreasing it in the other. This results in an asymmetric hysteresis curve. Exchange bias is crucial in applications like spin valves and magnetic recording media, where it's used to "pin" the magnetization of one layer in a specific direction.

28. What is the difference between intrinsic and extrinsic hysteresis loops?

Intrinsic hysteresis loops represent the magnetic behavior of a material without considering the effects of its shape or surrounding space. They plot the intrinsic magnetic induction (B - μ₀H) against the applied field (H). Extrinsic loops, on the other hand, include the effects of the material's shape and the surrounding space, plotting the total magnetic induction (B) against H. The difference is particularly important for materials with high permeability or in shapes that create significant demagnetizing fields.

29. How does magnetic annealing affect a material's hysteresis curve?

Magnetic annealing is a process where a material is heated and then cooled in the presence of a magnetic field. This treatment can significantly alter the material's hysteresis curve. It typically results in the development of a preferred magnetization direction, leading to a more square-shaped hysteresis loop with higher remanence in the annealing field direction. This process is used to engineer specific magnetic properties in materials for various applications, such as creating materials with high magnetic permeability.

30. What is the significance of the initial permeability in relation to the hysteresis curve?

Initial permeability is the slope of the initial magnetization curve at very low field strengths. It represents how easily a material can be magnetized from a demagnetized state. On the hysteresis curve, it's related to the steepness of the curve near the origin. Materials with high initial permeability show a rapid increase in magnetization with small applied fields, which is desirable in applications like magnetic shielding and low-field sensors. The initial permeability is often much higher than the permeability at other points on the hysteresis loop.

31. How do multi-phase magnetic materials affect the shape of the hysteresis curve?

Multi-phase magnetic materials, which contain two or more distinct magnetic phases, often exhibit complex hysteresis behavior. The resulting hysteresis curve is typically a combination of the curves of the individual phases. This can lead to unusual shapes, such as "wasp-waisted" loops or loops with multiple inflection points. The interaction between phases can result in exchange coupling effects, which may enhance or diminish certain magnetic properties. Understanding these complex curves is crucial in designing materials for specific applications, such as permanent magnets with enhanced energy products.

32. What is the relationship between the hysteresis curve and magnetic permeability?

Magnetic permeability, which measures a material's ability to support the formation of a magnetic field within itself, is directly related to the slope of the hysteresis curve. The permeability varies along the curve, with the highest permeability typically occurring in the steepest parts of the curve. The initial permeability is determined by the slope near the origin, while the maximum permeability corresponds to the point of maximum slope on the curve. Materials with high permeability have steeper curves and are more easily magnetized.

33. What is magnetic coercivity, and how is it determined from the hysteresis curve?

Magnetic coercivity, often simply called coercivity, is the intensity of the applied magnetic field required to reduce the magnetization of a material to zero after it has been magnetized to saturation. On the hysteresis curve, it's represented by the intercept on the H-axis (x-axis). There are actually two types of coercivity: the field required to reduce the magnetic flux density (B) to zero is called the B-coercivity, while the field required to reduce the magnetization (M) to zero is the H-coercivity. For most materials, these values are similar, but they can differ significantly in some cases.

34. How does the hysteresis curve change for nanoscale magnetic materials?

Nanoscale magnetic materials often exhibit significantly different hysteresis behavior compared to their bulk counterparts. As particle size decreases, the hysteresis loop typically becomes narrower, with reduced coercivity and remanence. This is partly due to the increased importance of surface effects and the reduction in the number of magnetic domains. Below a critical size (which depends on the material), particles can become superparamagnetic, showing no hysteresis at room temperature. Understanding these size-dependent effects is crucial in applications like magnetic nanoparticles for medical imaging and therapy.

35. What is the significance of the saturation magnetization in the hysteresis curve?

Saturation magnetization is the maximum induced magnetic moment that can be obtained in a magnetic field. On the hysteresis curve, it's represented by the flat upper and lower portions of the loop, where increasing the applied field no longer increases the magnetization. The saturation magnetization is an intrinsic property of the material and is important in determining the maximum energy product in permanent magnets. It also influences the shape of the entire hysteresis loop and is crucial in applications