Intrinsic Semiconductors - Undoped Semiconductors, Definition, Working Mechanism, FAQs

Edited By Vishal kumar | Updated on Jul 02, 2025 05:07 PM IST

The intrinsic semiconductors are the semiconductors that have no impurity in them. They are the purest form of semiconductors. They have no other element, such as doping, in them. There are the two types of semiconductors. In this article, we will discuss what intrinsic semiconductors are, the intrinsic semiconductor diagram for energy bands, the working mechanism of intrinsic semiconductors, examples of intrinsic semiconductors, the Fermi energy level and carrier concentration formula of intrinsic semiconductors, and intrinsic semiconductor current.

This Story also Contains

What are intrinsic semiconductors?
Example of Intrinsic Semiconductor
Working Mechanism of Intrinsic Semiconductors
Fermi Energy Level Of Intrinsic Semiconductor
Energy Band diagram for Intrinsic Semiconductor
Intrinsic Carrier Concentration
Intrinsic Semiconductor Current

Intrinsic Semiconductors - Undoped Semiconductors, Definition, Working Mechanism, FAQs

What are intrinsic semiconductors?

Intrinsic semiconductors are chemically pure semiconductors that are free of impurities. The intrinsic semiconductor behaves as an insulator at absolute zero temperature because all electrons are participating in covalent bonding. So, there are no free electrons. When temperature is provided to the material, the covalent bonds break down and a pair of electrons and holes are generated. These free electrons and holes lead the material to behave as a semiconductor. In an intrinsic semiconductor, the number of free electrons is equal to the number of holes, i.e., $n_e=n_h=n_i$. Another name for intrinsic semiconductors is undoped semiconductors or i-type semiconductors. So, we can say that a semiconductor in its purest form is called an intrinsic semiconductor.

Example of Intrinsic Semiconductor

Silicon: It is widely used in the production of electronics like diodes, transistors, and solar cells. Its band gap energy is 1.1 eV.
Germanium: It is used in high-speed transistors and infrared detectors. Germanium is sensitive to temperature variations, as the band gap energy is only 0.66 eV.

Working Mechanism of Intrinsic Semiconductors

Take, for example, a Si intrinsic semiconductor or Ge intrinsic semiconductor

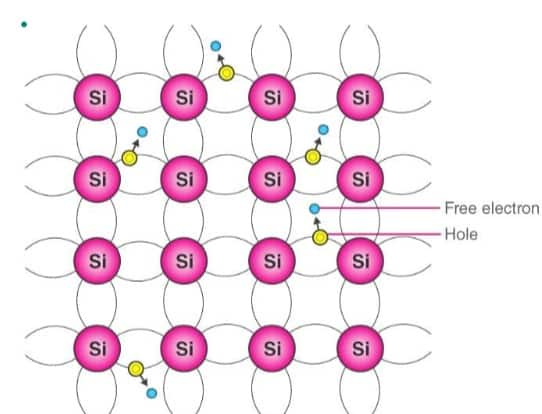
Both elements have four electrons in their outermost shell, or valence shell, as seen in their electron configurations. The electrons gather more thermal energy and consequently break away from their shell as the temperature of the semiconductor rises. The atoms in the crystal lattice are ionized, which causes a vacancy in the link between them. There is a hole in the position where the electron is dislodged, which is comparable to an effective positive charge. The hole is subsequently filled by a free electron, turning the previous vacant position into a hole and the former unoccupied position into a neutral position. The hole, or effective positive charge, is transferred from one place to another in this manner.

The number of free electrons in an intrinsic semiconductor is equal to the number of holes. So, $n_e=n_h=n_i$
The number of total intrinsic carrier concentration, which is equivalent to the total number of holes or electrons, is given by $n_i$.

When an intrinsic semiconductor's temperature is T=0 K, it behaves like an insulator. The electrons become excited and travel from the valence band to the conduction band when the temperature rises ($\mathrm{T}>0$).These electrons partially fill the conduction band, leaving an equivalent number of holes in the valence band.

Fermi Energy Level Of Intrinsic Semiconductor

The Fermi level is that energy level where the probability of finding an electron is 0.5 (50%) at absolute zero temperature, i.e., at T = 0 K (-273 ${ }^{\circ} \mathrm{C}$). The Fermi level is considered the highest energy state that can be occupied. The number of holes in the valence band in an intrinsic semiconductor is equal to the number of electrons in the conduction band. As a result, the probability of occupying energy levels in the valence and conduction bands is the same. So the middle of the forbidden energy band is the Fermi level in an intrinsic semiconductor.

Energy Band diagram for Intrinsic Semiconductor

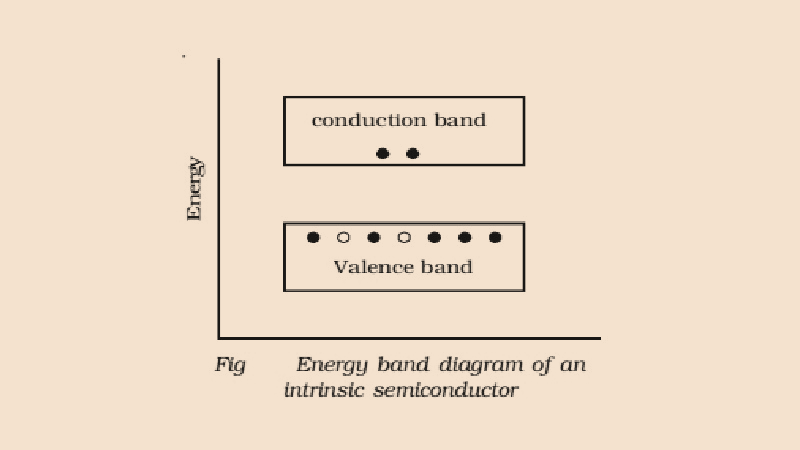
Intrinsic semiconductor energy band diagram

First, the conduction band was empty in the above energy band diagram, whereas the valence band was filled. Some heat energy can be delivered to it once the temperature has been raised. As a result of exiting the valence band, electrons from the valence band are supplied to the conduction band. The flow of electrons will be random as they move from the valence to the conduction band. The crystal's holes can also flow freely in any direction.

As a result, the TCR (temperature coefficient of resistance) of this semiconductor will be negative. The TCR indicates that when the temperature rises, the material's resistance decreases, and the conductivity of the intrinsic semiconductor rises. This shows the effect of temperature on the conductivity of intrinsic semiconductors.

Related Topics,

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Intrinsic Carrier Concentration

Two types of charge carriers are formed in intrinsic semiconductors when the valence electrons break the covalent bond and leap into the conduction band. Free electrons and holes are what they are. Carrier concentration in intrinsic semiconductors refers to the number of electrons per unit volume in the conduction band or the number of holes per unit volume in the valence band.

Electron-carrier concentration refers to the number of electrons per unit volume in the conduction band, while hole-carrier concentration refers to the number of holes per unit volume in the valence band. The number of electrons created in the conduction band in an intrinsic semiconductor is equal to the number of holes generated in the valence band.

As a result, the concentration of electron carriers is equal to the concentration of hole carriers. It can be written as,

$$
n=p=n_i
$$

Where,

n = electron-carrier concentration
P = hole-carrier concentration
$n_i$= intrinsic carrier concentration

Intrinsic Carrier Concentration Formula

In the valence band, hole concentration is expressed as

1642753309418 $$
\mathbf{p}=\mathbf{N}_{\mathrm{v}} \ \mathrm{e}^{\frac{-\left(\mathbf{E}_{\mathrm{f}}-\mathbf{E}_{\mathrm{v}}\right)}{\mathrm{K}_{\mathrm{b}} \mathbf{T}}}
$$

In the conduction band, electron concentration is expressed as

$$
\mathbf{n}=N_c \ e^{\frac{-\left(E_c-E_f\right)}{K_b T}}
$$

where, $K_B$ is the Boltzmann constant

$T$ = Absolute temperature of a pure semiconductor

$\mathrm{N}_{\mathrm{c}}$ = effective density of states in conduction band

$\mathrm{N}_{\mathrm{v}}$ = effective density of states in valence band

Intrinsic Semiconductor Current

Electric current flows due to both electron and hole movements in intrinsic semiconductors, i.e., electrons in the conduction band that have been released from their lattice locations can travel through the material. Other electrons can also jump between lattice positions to fill the voids created by the released electrons. The holes seem to migrate in the opposite direction of the free electrons across the material; this extra mechanism is known as hole conduction. The density of energy levels determines the electron density in the conduction band, which affects current flow in an intrinsic semiconductor. This current is extremely temperature-sensitive.

Condition of Intrinsic Semiconductor at Room Temperature

At room temperature, an intrinsic semiconductor has a few free electrons and holes. So, there is a flow of current, but this current is low. While an intrinsic or pure semiconductor behaves like an insulator at absolute zero temperature because all electrons are participating in covalent bonding. So, there are no free electrons to participate in charge transfer. When thermal energy is provided to the material, the covalent bonds break down and a pair of electrons and holes is generated. These free electrons and holes lead the material to behave as a semiconductor. The conductivity of an intrinsic semiconductor decreases with a decrease in temperature, so it behaves as an insulator at absolute zero temperature (0 Kelvin).

Doping

The addition of impurities to a semiconductor is known as doping. During the preparation of an extrinsic semiconductor, the amount of impurity injected into the material must be controlled. A semiconductor can have one impurity atom added to every 108 atoms. The number of holes or electrons can be increased by introducing the impurity to improve its conductivity. If a pentavalent impurity with 5 valence electrons is added to a pure semiconductor, then it will be a p-type extrinsic semiconductor, while if a trivalent impurity is added to a pure semiconductor, then it will be an n-type semiconductor. On this basis, extrinsic semiconductors are categorized into two types: n-type and p-type semiconductors.

Also read:

Frequently Asked Questions (FAQs)

1. What are intrinsic semiconductor or intrinsic semiconductor definition?

Intrinsic semiconductors are made of the purest semiconductor material.

2. What is the difference between an intrinsic and an extrinsic semiconductor?

The intrinsic type of semiconductor is pure, whereas the extrinsic type is one that can have impurities introduced to make it conductive.

3. What are some intrinsic type examples?

Silicon and germanium are the two elements.

4. How does intrinsic conductivity work?

The intrinsic conductivity of a semiconductor is defined as the concentration of impurities and structural flaws in the semiconductor.

5. At normal temperature, what do intrinsic semiconductors employ for conduction?

Electrons and holes are employed in this experiment.

6. What are limitations of Intrinsic semiconductors?

Intrinsic semiconductors exhibit low conductivity at room temperature, as there are no impurities in these semiconductors.

7. What is energy band gap?

The energy difference between the topmost of the valence band and the lowest of the conduction band is known as the energy band gap for any semiconductor.

8. What are the applications of Intrinsic semiconductors?

The intrinsic semiconductors are used in making transistors.

9. What does a hole represent in an Intrinsic semiconductor?

A hole represents the absence of an electron in any semiconductor.

10. Which part of electron-hole pair is responsible for conduction in Forward bias or reverse bias?

The electron is responsible for the flow of current during the forward bias, while the hole is responsible for the flow of current during the reverse bias process.

11. What is an intrinsic semiconductor?

An intrinsic semiconductor is a pure semiconductor material that has not been doped with impurities. It contains an equal number of electrons in the conduction band and holes in the valence band at room temperature. Silicon and germanium are common examples of intrinsic semiconductors.

12. How does the band structure of an intrinsic semiconductor differ from that of an insulator?

In an intrinsic semiconductor, the band gap (energy difference between the valence band and conduction band) is smaller than in an insulator. This allows some electrons to be thermally excited from the valence band to the conduction band at room temperature, creating electron-hole pairs. In insulators, the band gap is much larger, making it difficult for electrons to cross.

13. Why are intrinsic semiconductors called "undoped" semiconductors?

Intrinsic semiconductors are called "undoped" because they are pure materials without intentionally added impurities. Their electrical properties are determined solely by the inherent characteristics of the semiconductor material itself, rather than by introduced dopants.

14. What is the Fermi level in an intrinsic semiconductor?

In an intrinsic semiconductor, the Fermi level is located approximately halfway between the valence band and the conduction band. This position represents the energy level at which the probability of finding an electron is 0.5 at thermal equilibrium.

15. How does temperature affect the conductivity of an intrinsic semiconductor?

As temperature increases, the conductivity of an intrinsic semiconductor increases. This is because higher temperatures provide more thermal energy, allowing more electrons to be excited from the valence band to the conduction band, creating more charge carriers (electrons and holes).

16. What is the primary charge transport mechanism in intrinsic semiconductors?

In intrinsic semiconductors, charge transport occurs through both electrons in the conduction band and holes in the valence band. Electrons move through the conduction band, while holes (which represent the absence of electrons) effectively move through the valence band in the opposite direction.

17. How does the energy band gap affect the properties of an intrinsic semiconductor?

The energy band gap determines many properties of an intrinsic semiconductor. A smaller band gap allows for easier electron excitation, resulting in higher conductivity at room temperature. It also affects the semiconductor's optical properties, determining the energy of photons that can be absorbed or emitted.

18. What is electron-hole pair generation in intrinsic semiconductors?

Electron-hole pair generation is the process where an electron is excited from the valence band to the conduction band, leaving behind a hole in the valence band. This can occur due to thermal energy or absorption of a photon with energy equal to or greater than the band gap.

19. How does the concept of effective mass apply to charge carriers in intrinsic semiconductors?

Effective mass is a concept used to describe how electrons and holes move within the crystal lattice of a semiconductor. It accounts for the interaction between the charge carriers and the periodic potential of the crystal. The effective mass can be different from the actual mass of an electron and affects the mobility of charge carriers.

20. What is the significance of the intrinsic carrier concentration in semiconductors?

The intrinsic carrier concentration (ni) represents the number of electrons in the conduction band (or holes in the valence band) per unit volume in an intrinsic semiconductor at a given temperature. It's a crucial parameter that determines the electrical properties of the semiconductor and varies with temperature and band gap energy.

21. How does the intrinsic carrier concentration change with temperature?

The intrinsic carrier concentration increases exponentially with temperature. This is because higher temperatures provide more thermal energy for electrons to be excited across the band gap, creating more electron-hole pairs.

22. What is meant by "intrinsic region" in a semiconductor device?

The intrinsic region in a semiconductor device refers to an undoped or lightly doped area of semiconductor material. This region is often used in devices like PIN diodes or certain types of solar cells to create a depletion region with specific electrical characteristics.

23. How does the resistivity of an intrinsic semiconductor compare to that of metals and insulators?

The resistivity of an intrinsic semiconductor is typically between that of metals and insulators. It's higher than metals due to fewer free charge carriers, but lower than insulators because some charge carriers can be thermally excited across the smaller band gap.

24. What role does crystal structure play in the properties of intrinsic semiconductors?

The crystal structure of intrinsic semiconductors, typically a diamond cubic lattice for silicon and germanium, determines the arrangement of atoms and the nature of chemical bonds. This structure influences the energy band formation, electron mobility, and other electrical and optical properties of the semiconductor.

25. How does quantum mechanics explain the behavior of electrons in intrinsic semiconductors?

Quantum mechanics describes electrons in semiconductors as wave-like entities occupying discrete energy states. It explains phenomena like the formation of energy bands, the probabilistic nature of electron excitation across the band gap, and quantum tunneling effects in certain semiconductor devices.

26. What is the difference between direct and indirect band gap in intrinsic semiconductors?

In direct band gap semiconductors, the minimum of the conduction band aligns with the maximum of the valence band in momentum space, allowing direct electron transitions. In indirect band gap semiconductors, these points don't align, requiring phonon assistance for transitions. This affects optical and electrical properties, particularly in light emission and absorption processes.

27. How does carrier mobility differ between electrons and holes in intrinsic semiconductors?

In most intrinsic semiconductors, electron mobility is higher than hole mobility. This is because electrons in the conduction band typically have a smaller effective mass compared to holes in the valence band, allowing them to move more freely through the crystal lattice under an applied electric field.

28. What is the significance of the intrinsic Fermi level in semiconductor physics?

The intrinsic Fermi level represents the energy at which the probability of electron occupancy is exactly 0.5 in an intrinsic semiconductor. It's crucial for understanding the energy distribution of electrons and holes, and it plays a key role in determining the electrical behavior of semiconductor devices.

29. How does the concept of drift current apply to intrinsic semiconductors?

Drift current in intrinsic semiconductors refers to the movement of charge carriers (both electrons and holes) under the influence of an applied electric field. The magnitude of this current depends on the carrier concentration, mobility, and the strength of the electric field.

30. What is the role of phonons in intrinsic semiconductor behavior?

Phonons, which are quantized lattice vibrations, play several important roles in intrinsic semiconductors. They assist in indirect band gap transitions, contribute to charge carrier scattering (affecting mobility), and are involved in heat transport within the semiconductor material.

31. How does the law of mass action apply to intrinsic semiconductors?

The law of mass action in intrinsic semiconductors states that the product of electron and hole concentrations is constant at a given temperature. This means that n * p = ni^2, where n is the electron concentration, p is the hole concentration, and ni is the intrinsic carrier concentration.

32. What is the significance of the intrinsic Debye length in semiconductor physics?

The intrinsic Debye length is a characteristic length scale in semiconductors that describes how far the electric field of a charge carrier penetrates into the material. It's important for understanding charge screening effects and the behavior of space charge regions in semiconductor devices.

33. How does band bending occur at the surface of an intrinsic semiconductor?

Band bending at the surface of an intrinsic semiconductor occurs due to the presence of surface states. These states can trap charges, creating a space charge region near the surface. This results in the energy bands curving up or down near the surface, affecting the material's electrical properties in that region.

34. What is the difference between equilibrium and non-equilibrium carrier concentrations in intrinsic semiconductors?

Equilibrium carrier concentrations in intrinsic semiconductors are the electron and hole concentrations present under thermal equilibrium conditions. Non-equilibrium concentrations occur when the semiconductor is disturbed from equilibrium, such as under illumination or applied voltage, resulting in excess carriers.

35. How does the concept of recombination lifetime apply to intrinsic semiconductors?

Recombination lifetime in intrinsic semiconductors refers to the average time an excess electron-hole pair exists before recombining. It's a crucial parameter that affects the electrical and optical properties of the material, particularly in processes involving light absorption or carrier injection.

36. What is the significance of the intrinsic Fermi velocity in semiconductor physics?

The intrinsic Fermi velocity is the average velocity of electrons at the Fermi level in a semiconductor. It's an important parameter in understanding charge transport phenomena, particularly in high-field conditions or in nanoscale semiconductor devices where ballistic transport may occur.

37. How does quantum confinement affect the properties of intrinsic semiconductors at nanoscale dimensions?

Quantum confinement occurs when the size of a semiconductor structure becomes comparable to the de Broglie wavelength of the charge carriers. This leads to discretization of energy levels, widening of the band gap, and changes in optical and electrical properties, which are not observed in bulk intrinsic semiconductors.

38. What is the role of effective density of states in intrinsic semiconductor behavior?

The effective density of states represents the number of available energy states for electrons in the conduction band or holes in the valence band. It's crucial for calculating carrier concentrations and understanding how charge carriers distribute themselves energetically within the bands.

39. How does the intrinsic carrier concentration affect the operation of semiconductor devices?

The intrinsic carrier concentration influences many aspects of semiconductor device operation, including leakage currents, threshold voltages in transistors, and the sensitivity of devices to temperature changes. Higher intrinsic carrier concentrations generally lead to increased leakage and temperature sensitivity.

40. What is the difference between drift and diffusion currents in intrinsic semiconductors?

Drift current results from the movement of charge carriers under an applied electric field, while diffusion current arises from the movement of carriers due to concentration gradients. Both contribute to the total current in semiconductor devices, with their relative importance depending on the specific device and operating conditions.

41. How does the concept of generation-recombination balance apply to intrinsic semiconductors?

In thermal equilibrium, the rate of electron-hole pair generation in an intrinsic semiconductor exactly balances the rate of recombination. This balance maintains a constant intrinsic carrier concentration. When disturbed from equilibrium, the semiconductor will tend to return to this balanced state through net generation or recombination processes.

42. What is the significance of the intrinsic Debye screening length in semiconductor physics?

The intrinsic Debye screening length is the characteristic distance over which mobile charge carriers screen out electric fields in the semiconductor. It's important for understanding how electric fields penetrate the material and how charge distributions behave, particularly in the context of junctions and interfaces.

43. How does the band structure of an intrinsic semiconductor change under applied stress or strain?

Applied stress or strain can modify the band structure of an intrinsic semiconductor. It can change the band gap, alter the effective masses of carriers, and even transform an indirect band gap semiconductor into a direct one under certain conditions. This phenomenon is the basis for strain engineering in semiconductor devices.

44. What is the role of phonon scattering in determining carrier mobility in intrinsic semiconductors?

Phonon scattering is a primary mechanism limiting carrier mobility in intrinsic semiconductors at room temperature. As charge carriers move through the crystal, they interact with lattice vibrations (phonons), which causes them to change direction and velocity, effectively reducing their mobility.

45. How does the concept of minority and majority carriers apply to intrinsic semiconductors?

In a truly intrinsic semiconductor, the concepts of minority and majority carriers don't apply because the concentrations of electrons and holes are equal. However, even slight unintentional doping or temperature variations can create a small imbalance, leading to one type of carrier becoming the majority.

46. What is the significance of the intrinsic level (Ei) in semiconductor band diagrams?

The intrinsic level (Ei) in semiconductor band diagrams represents the energy level at which the Fermi level would lie in an intrinsic semiconductor. It's a reference point for understanding how doping and other factors affect the position of the Fermi level and, consequently, the electrical properties of the semiconductor.

47. How does the concept of carrier freeze-out apply to intrinsic semiconductors at low temperatures?

Carrier freeze-out occurs at very low temperatures when thermal energy is insufficient to excite electrons across the band gap. In intrinsic semiconductors, this leads to a dramatic decrease in carrier concentration and conductivity as temperature approaches absolute zero.

48. What is the role of the density of states function in describing intrinsic semiconductor properties?

The density of states function describes the number of available energy states per unit energy interval in a semiconductor. It's crucial for calculating carrier concentrations, understanding optical absorption and emission processes, and determining how carriers distribute themselves energetically within the bands.

49. How does the concept of effective mass anisotropy affect charge transport in intrinsic semiconductors?

Effective mass anisotropy means that the effective mass of carriers varies depending on the direction of movement within the crystal. This anisotropy affects charge transport properties, leading to direction-dependent mobility and influencing the design of semiconductor devices where carrier transport direction is important.

50. What is the significance of the intrinsic diffusion length in semiconductor physics?

The intrinsic diffusion length is the average distance that excess carriers (electrons or holes) can diffuse before recombining in an intrinsic semiconductor. It's an important parameter in understanding carrier transport and recombination processes, particularly in devices like solar cells and photodetectors.

51. How does the concept of velocity saturation apply to charge carriers in intrinsic semiconductors?

Velocity saturation occurs when the drift velocity of charge carriers no longer increases linearly with the applied electric field, instead approaching a maximum value. This phenomenon becomes important in high-field conditions and affects the performance of high-speed semiconductor devices.

52. What is the role of trap states in intrinsic semiconductors?

Trap states are energy levels within the band gap that can capture and release charge carriers. In intrinsic semiconductors, these states can arise from crystal defects or impurities. They affect carrier lifetimes, recombination rates, and can influence the electrical and optical properties of the material.

53. How does the concept of ambipolar diffusion apply to intrinsic semiconductors?

Ambipolar diffusion occurs when electrons and holes diffuse together in a semiconductor to maintain charge neutrality. In intrinsic semiconductors, where electron and hole concentrations are equal, this process ensures that both types of carriers move at the same effective rate under concentration gradients.

54. What is the significance of the intrinsic carrier lifetime in semiconductor devices?

The intrinsic carrier lifetime is the average time an excess electron-hole pair exists before recombining in an intrinsic semiconductor. It's crucial for understanding and optimizing devices that rely on excess carrier generation, such as solar cells and photodetectors, as it affects the collection efficiency of these carriers.

55. How does the concept of band tailing apply to intrinsic semiconductors?

Band tailing refers to the extension of energy states into the band gap from both the conduction and valence bands. In intrinsic semiconductors, it can arise from disorder in the crystal structure or thermal effects. Band tailing can affect optical absorption properties and carrier transport, especially near the band edges.

56. What is the role of surface states in the behavior of intrinsic semiconductors?

Surface states are energy levels that exist at the surface of a semiconductor due to the abrupt termination of the crystal lattice. In intrinsic semiconductors, these states can trap charges, leading to band bending near the surface and affecting the material's electrical properties in that region.

57. How does the concept of hot carriers apply to intrinsic semiconductors under high electric fields?

Hot carriers are charge carriers with energy significantly above the thermal equilibrium energy. In intrinsic semiconductors under high electric fields, carriers can gain enough energy to overcome the average scattering processes, leading to non-equilibrium transport phenomena and potentially impacting device performance.

58. What is the significance of the intrinsic Fermi-Dirac distribution in semiconductor physics?

The intrinsic Fermi-Dirac distribution describes the probability of electron occupancy at different energy levels in an intrinsic semiconductor at thermal equilibrium. It's fundamental to understanding how carriers distribute themselves energetically and is crucial for calculating carrier concentrations and other electronic properties.

59. How does the concept of impact ionization apply to intrinsic semiconductors?

Impact ionization occurs when a high-energy carrier collides with a lattice atom, creating an electron-hole pair. In intrinsic semiconductors, this process can lead to carrier multiplication under high electric fields, which is important in devices like avalanche photodiodes and certain types of high-power semiconductor devices.

60. What is the role of the intrinsic dielectric constant in semiconductor behavior?

The intrinsic dielectric constant of a semiconductor determines how the material responds to electric fields. It affects the strength of coulomb interactions between charges, influences the behavior of space charge regions, and plays a role in determining capacitance