Isothermal Process - Definition, Example, Formula, FAQs

In this article, we will discuss the Isothermal Process which is a thermodynamic process in which the temperature of a system remains constant throughout the process. In real life, we can observe isothermal processes in refrigeration and air conditioning systems, where gases are compressed and expanded while maintaining a constant temperature to regulate cooling. Let's discuss the concept of the Isothermal process in detail

This Story also Contains

1. What is an Isothermal Process?
2. Isothermal Process Formula
3. Work Done in the Isothermal Process
4. PV Diagram for the Isothermal Process
5. Isothermal Process Examples
6. Solved Examples of Isothermal Process

What is an Isothermal Process?

An isothermal process is a type of thermodynamic process where the temperature of the system remains constant throughout the entire process. In this process, the system exchanges heat with its surroundings to maintain this constant temperature, despite changes in other properties like pressure or volume

What is Isotherm?

If we observe the relation between temperature and any other thermodynamic variable such as pressure, volume, and others and draw a graph on the Cartesian plane then, all the curves which represent two states of a system where the temperature is the same during an isothermal process are called isotherms.

So, Those curves or lines which represent two states of a system at the same temperature in an isothermal process are called an isotherm.

For example, a line drawn as shown in the diagram below has two states A and B and both are at the same temperature during an isothermal process so this line is called an isotherm. We can consider any other thermodynamic variable on the X-axis.

Also read -

• NCERT Solutions for All Subjects
• NCERT Notes For All Subjects
• NCERT Exemplar Solutions for All Subjects

Isothermal Process Formula

The basic formula in thermodynamics which shows that two states are in the isothermal process is simply written as

$P_1 V_1=P_2 V_2$

where,

• P represents the pressure and
• V represents the volume of an isothermal process in two states 1 and 2

Work Done in the Isothermal Process

When a system undergoes an isothermal process, either work is done on it or work is done by it and this work is different for different processes.

In the isothermal process work done by the system is calculated using the formula:

$W=2.303 R T \log _{10}\left(V_2 N_1\right)$

where,

• V represents volume at two different states being at a constant temperature of T and R is the universal gas constant.

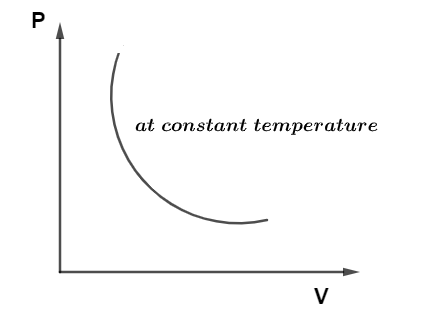
PV Diagram for the Isothermal Process

A diagram representation of the pressure and volume of an isothermal process on a cartesian plane is called a PV diagram for an isothermal process and it is best shown in the diagram given below:

Change in Internal Energy in the Isothermal Process

The internal energy of any thermodynamic system is calculated as

∆U=nCv∆T

where,

• n represents the total number of moles of a gas
• C represents the specific heat of the gas but at constant volume
• T represents temperature

Related Terms

• Adiabatic process
• Second Law Of Thermodynamics
• Isochoric Process
• Specific Heat Of A Gas
• Entropy

In an isothermal process, the change in temperature is zero because of the constant temperature in the isothermal process. So, In an isothermal process, the change in internal energy is zero.

Recommended Topic Video

Isothermal Process Examples

1. When ice melts at a temperature of zero degrees then the whole ice melts but the temperature of the system remains the same over the period of time, hence this is an example of an isothermal process.
2. All the thermodynamic reactions which occur inside the refrigerator are isothermal processes because the temperature of the refrigerator remains the same.
3. and, all such thermodynamic processes which are carried out at constant magnitude of temperature will be considered as isothermal processes.

Solved Examples of Isothermal Process

1- Which of the following statements correctly describes the relationship between the slope of the isothermal curve and the slope of the adiabatic curve for a gas process?
1. Slope of the isothermal curve = Slope of the adiabatic curve
2. Slope of the isothermal curve $=\gamma \times$ Slope of the adiabatic curve
3. Slope of the adiabatic curve $=\gamma \times$ Slope of the isothermal curve
4. Slope of the adiabatic curve $=\frac{1}{2 \gamma} \times$ Slope of the isothermal curve

Solution:

Differentiating $P V=$ constant:

$$
\frac{d P}{d V}=-\frac{P}{V}
$$
Hence, the slope of the isothermal curve is:

$$
\text { Slope of isothermal curve }=-\frac{P}{V} \text {. }
$$
Differentiating $P V^\gamma=$ constant:

$$
\frac{d P}{d V}=-\gamma \frac{P}{V}
$$
Hence, the slope of the adiabatic curve is:

$$
\text { Slope of adiabatic curve }=-\gamma \frac{P}{V} .
$$

From the equations above:

$$
\left(\frac{d P}{d V}\right)_{\text {adiabatic }}=\gamma\left(\frac{d P}{d V}\right)_{\text {isothermal }} .
$$
Hence, the answer is the option 3.

2- 2 moles of an ideal is isothermally expanded to 3 times its original volume at 300 K . Calculate the Work done and heat absorbed by the gas?
Given ( $\mathrm{R}=8.31 \mathrm{~J} / \mathrm{mol}-\mathrm{K}$ and $\log _e 3=.4771$ )
Solution:
Here $\mathrm{n}=3, V_2=3 V_1, \mathrm{~T}=300 \mathrm{~K}$
Now using the above equation

$$
W=n R \operatorname{Tln}\left(\frac{V_2}{V_1}\right)
$$

Substituting the above values, we get

$$
W=5.48 \times 10^3 \mathrm{~J}
$$

Now heat absorbed $=$ Work done $=5.48 \times 10^3 \mathrm{~J}=1.31 \times 10^3 \mathrm{C}$

3. Draw the T-P diagram for the given P-V diagram for an ideal gas.

Solution:
$$
P=\frac{\text { constant }}{V}
$$or$$
P V=\mathrm{constant}
$$

So it means temperature is constant. So here is the TP diagram