Kirchhoff's Second Law

Kirchhoff's Second Law, also known as the Voltage Law or Kirchhoff's Loop Rule, is a fundamental principle in electrical circuits. It states that the sum of all the electric potential differences (voltages) around any closed loop in a circuit is equal to zero. This means that the total energy gained by charges in a loop must equal the total energy lost, ensuring energy conservation in electrical circuits.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. What is Kirchoff's Second Law?
2. Solved Examples Based on Kirchoff's Second Law
3. Summary

In this article, we will discuss the Kirchhoff's second law. It is an important concept of current electricity for those who are preparing for class 12, NEET and JEE MAIN exams. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of eleven questions have been asked on this concept. And for NEET five questions were asked from this concept.

What is Kirchoff's Second Law?

The algebraic sum of all the potential across a closed loop is zero. This law is also known as Kirchhoff's Voltage law (KVL)

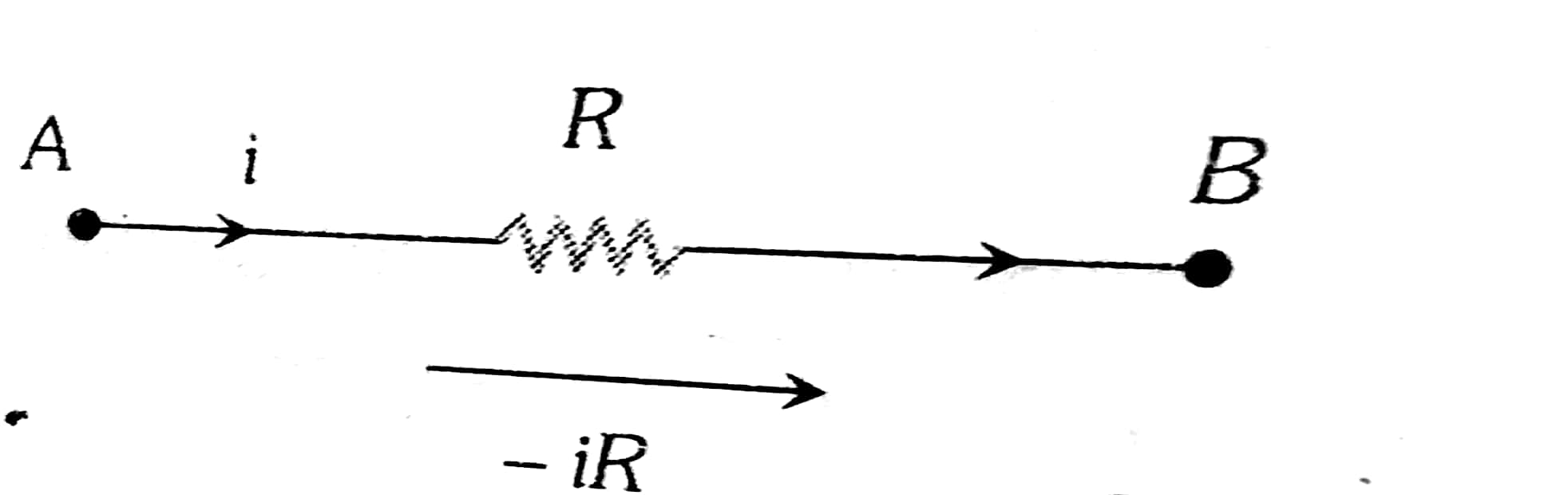
Change in Potential in traversing a resistance is - iR

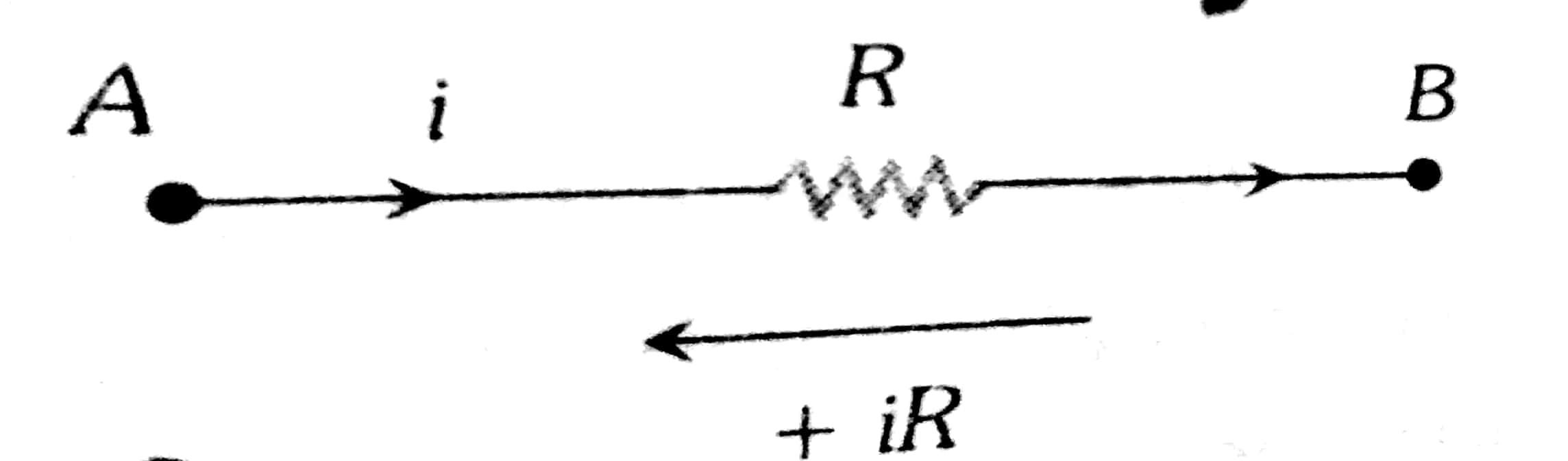
Change in Potential in the opposite direction is - iR

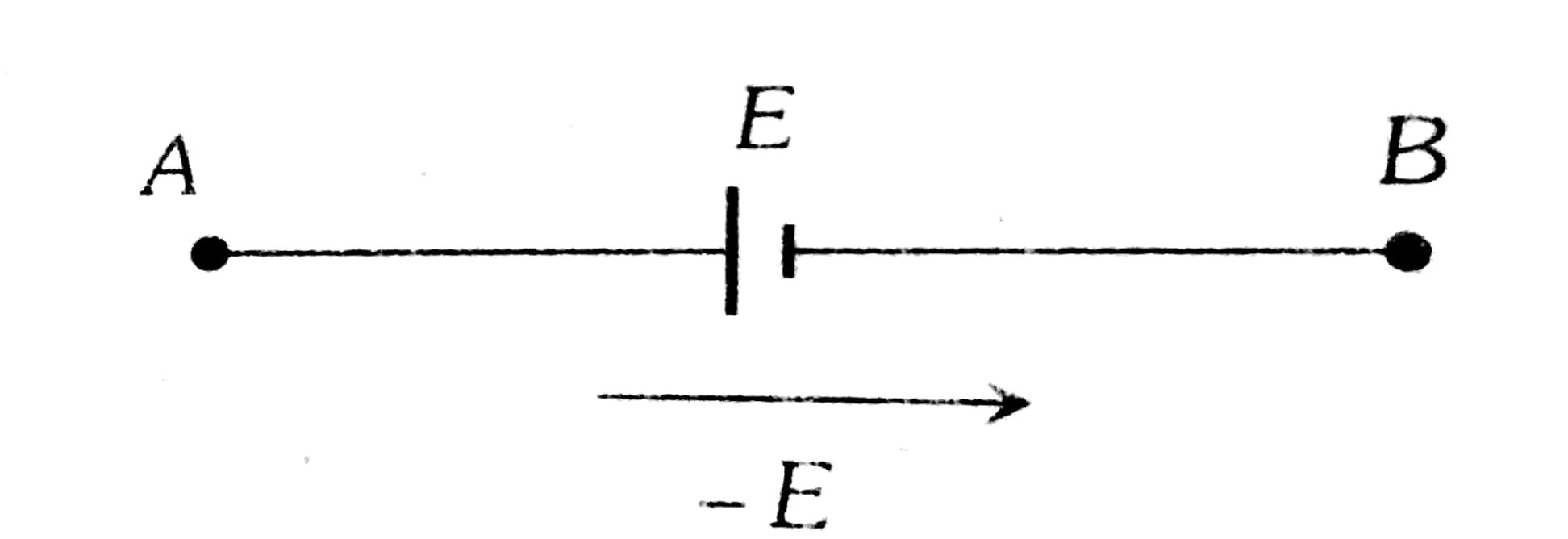
Traversing an e.m.f source from negative to positive terminal is -E

While in the opposite direction is E

Change in Potential in traversing a capacitor from negative to positive qC

While in the opposite direction is −qC

In closed-loop

−i1R1+i2R2−E1−i3R3+E2+E3−i4R4=0

For More Information On Kirchoff's Second Law, Watch The Below Video:

Solved Examples Based on Kirchoff's Second Law

Example 1: potential difference (in V )across 2Ω resistor in the given circuit is:

1) -1

2) -2

3) -3

4) -4

Solution:

Change in Potential in traversing a resistance

-i R

wherein

Apply KVL

4−I∗1+2−3∗I−3−2∗I=0⇒6I=3 or ⇒I=12 P.D. across 2Ω=−IR=−12∗2V=−1V

Hence, the answer is option (1).

Example 2: The potential difference between points a and b is

1) +45V
2) −45 V
3) +35 V
4) −35V

Solution:

Change in Potential in the opposite direction -

+i R

wherein

Apply KVL

15−I∗1−1−2I−6−4I−3I=0 or 8=10I or I=45A∴Va−Vb=+IR=+45V

Hence, the answer is option (1).

Example 3: Figure represents part of a closed circuit. The potential difference VA−VB is gin volts)

1) 1

2) 18

3) 6

4) 24

Solution:

Traversing an e.m.f source from negative to positive terminal

wherein

VA+3−3∗1−3∗6=VB
or VA−VB=18 V

Hence, the answer is option (2).

Example 4: In the given circuit, with a steady current, the potential drop across the capacitor must be

1) V

2) V/2

3) V/3

4) 2V/3

Solution:

Change in Potential in traversing a capacitor from negative to positive

wherein

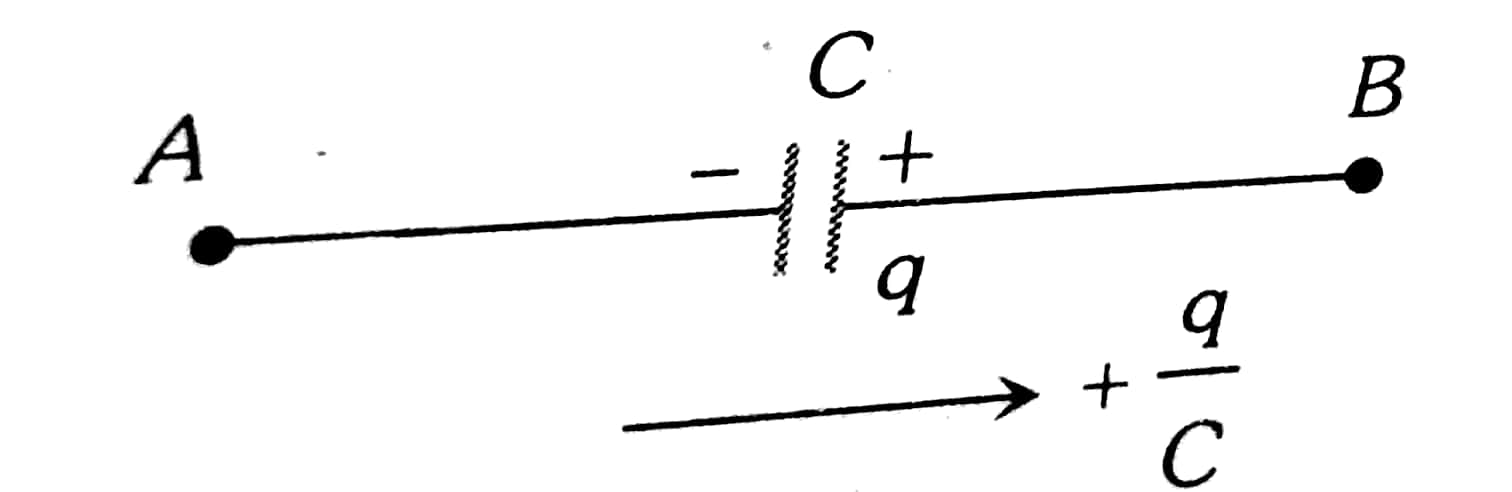
In the steady state conduction, no current will flow through the capacitor C.

I=2V−V2R+R=V3R
P.D between A&B is
VA−V+V+IR=VB or VB−VA=IR=V3

Hence, the answer is option (3).

Example 5: In the given circuit the cells have zero internal resistance. The currents (in Amperes ) Passing through resistance and respectively, are :

1) 1,2

2) 2,2

3) 0.5,0

4) 0, 1

Solution:

Kirchhoff's second law

The algebraic sum of all the potential across a closed loop is zero. This law is also known as Kirchhoff's Voltage law (KVL)

∴i1⇒VB−VAR1⇒1020⇒0.5Amp.∴i2⇒Vc−VAR2=0Amp.
current through R1=I1=0.5 A
current through R2=I2=0 A

Hence, the answer is option (3).

Summary

Kirchhoff's Second Law is essential for analyzing electrical circuits. It is also called the Voltage Law or Kirchhoff's Loop Rule. According to it, the sum of electromotive forces (emf) and potential differences (voltage drops) in a closed loop circuit equals zero. As a result of this law, all energy supplied by sources is equal to that consumed by components in the cycle, hence ensuring that there is no inferiority in terms of power levels around it.