Newton's Laws of Motion - Notes, Topics, Formulas, Books, FAQs
Laws of Motion is an important chapter of the Class 11 Physics syllabus, which concerns the connection between motion and the forces which cause the motion to occur. The chapter describes to students the effect of forces on the motion of the bodies and the interrelation between concepts of inertia, momentum and acceleration. Physics observes motion using the Newton laws of motion, which offer a systematic approach to the behaviour of objects in real-life situations.
This Story also Contains
- Important Topics of Laws of Motion
- Important Formulas of Laws of Motion
- Laws of Motion: Previous Year Questions
- Laws of Motion in Different Exams
- Important Books and Resources for Class 11 Laws of Motion
- NCERT Resources for Laws of Motion
- NCERT Subject-Wise Resources
- Practice Questions based on Laws of Motion
- Conclusion

The laws of motion cannot be studied effectively without the proper definition of a force, mass, acceleration, momentum and time. It is not sufficient to observe motion without determining what causes that motion and measuring it. Likewise, the relationship between bodies cannot be studied without introducing the relations between force and the resulting change in motion. The study of mechanical interactions can be done properly and with uniformity by using standard definitions and well-known laws. Besides this, the chapter also talks of other key concepts like the first, second, and third laws of motion by Newton, friction, and conservation of momentum. It emphasises the way these laws are found to be supported by experimental observations and how they can be applied to a large variety of physical phenomena. Learning the principles of motion makes students understand how to connect theory with the practical world and provides a good basis to further subject matters in mechanics and classical physics.
Important Topics of Laws of Motion
The important topics of the chapter Laws of Motion explain the fundamental principles that govern the motion of objects under the action of forces. In these topics, the concepts of force, inertia, momentum and friction are presented, and they are utilised to learn how and why bodies move or do not move. They provide a logical framework to analyse real-life situations involving motion and interaction between bodies.
1 Newton’s First Law of Motion (Law of Inertia)
According to Newton's First Law, a body that is in motion or at rest stays in its position in a straight line unless an external force unbalanced acts on it. This law gives rise to the concept referred to as inertia, which refers to the reluctance of any body to change its state of motion. The inertia is dependent on the mass of the body--the higher the mass, the higher the inertia. This law clarifies the necessity of seat belts and the reason why passengers are likely to be thrown forward in case a moving car is suddenly stopped.
2. Newton’s Second Law of Motion
According to Newton Second law, the acceleration of the momentum of a body is directly proportional to the force exerted on the body, and it acts in the same direction as the force. It is mathematically given as F=dp/dt.
In the case of constant mass, we have F =ma. This law gives the quantitative definition of force and finds innumerable uses in solving problems of acceleration, tension, friction, and applied forces.
3. Newton’s Third Law of Motion
The Third Law of Newton says that to every action there must be a reaction. These forces always act on different bodies and occur simultaneously. This law accounts for the different phenomena in real life, like walking, swimming, recoil in a gun, and the propulsion of rockets. It also provides the foundation of the conservation of momentum in isolated systems.
4. Linear Momentum
Linear momentum can be defined as the product of the mass of a body and its velocity, which is equal to p=mv. It is a vector quantity and plays a central role in the laws of motion. Momentum is a quantity that is dependent on mass and velocity, and hence it can be utilised in the study of collisions and interactions between bodies. The concept of momentum helps relate force with motion over a period of time.
5. Law of Conservation of Linear Momentum
According to the law of conservation of linear momentum, the total momentum of an isolated system is constant, provided no external force is applied on the system. This law is based on Newton's Third Law, and it is commonly used in collision problems, explosions, and rocket cases. It can be applied especially in cases where the forces during interaction are not known or complicated.
6. Friction
Friction is the tendency or force which resists relative movement or inclination of movement between two surfaces coming into contact. It develops as a result of the interlocking of microscopic irregularities on surfaces. There are other types of friction, such as static friction, kinetic friction and rolling friction. Friction leads to wastage of energy in machines, but it is necessary in walking, writing, and braking.
7. Static and Kinetic Friction
When a body is at rest, the friction is said to be static, and it prevents bodies to start moving, whereas when the body is already moving, the friction is said to be kinetic. The value of maximum friction (static) is proportional to the normal reaction. Kinetic friction tends to be smaller than limiting static friction and is almost constant at the time of movement. These forces are instrumental in the determination of problems of blocks on rough surfaces.
8. Rolling Friction
Rolling friction is experienced when a body slides over a surface, and it is significantly smaller than the sliding friction. That is why cars and machinery use wheels. Rolling friction is based on the deformation of the surfaces and not on the roughness. This is one of the concepts that can be used to explain the efficiency of transportation systems in terms of energy.
9. Free Body Diagram (FBD)
A free body diagram is a diagrammatic illustration of all external forces on a body. The most crucial and first step in the solution of the problems associated with the laws of Newton is to draw an accurate FBD. It assists in establishing the forces of weight, normal, tension, friction and applied forces distinctly. With correct FBDs, correct equations of motion are obtained.
- Gravitational force: The weight of a body acts downwards.
- Normal force: Perpendicular reaction from a surface.
- Friction: Opposes relative motion.
- Tension: Force in strings or ropes.
- Centripetal force: Keeps bodies in circular motion.
10. Equilibrium of Forces
A particle is said to be in equilibrium when it remains at rest or moves with uniform velocity, i.e., there is no acceleration.
Condition for Equilibrium
A particle is in equilibrium if the net force acting on it is zero:
A particle is in equilibrium if the net force acting on it is zero
$
\sum \vec{F}=0
$
In two dimensions, this condition can be written as:
$
\sum F_x=0 \quad \text { and } \quad \sum F_y=0
$
In three dimensions:
$
\sum F_x=0, \quad \sum F_y=0, \quad \sum F_z=0
$
Types of Equilibrium
1. Stable Equilibrium: If displaced, the particle returns to its original position.
Example: A ball at the bottom of a bowl.
2. Unstable Equilibrium: If displaced, the particle moves further away.
Example: A ball on top of a hill.
3. Neutral Equilibrium: If displaced, the particle stays in the new position.
Example: A ball on a flat surface.
11. Inertial and Non-Inertial Frames of Reference
An inertial frame of reference is one in which Newton’s laws are valid, while a non-inertial frame is an accelerating frame where Newton’s laws do not hold unless pseudo-forces are introduced. Understanding these frames helps analyse motion from different perspectives, such as motion inside accelerating vehicles. This topic builds the foundation for advanced mechanics.
Important Formulas of Laws of Motion
The formulas of the chapter Laws of Motion express the fundamental relationships between force, mass, acceleration, momentum, and friction. These equations provide a mathematical framework to analyse the effect of forces on the motion of bodies. Proper understanding and application of these formulas are essential for solving numerical problems accurately. Mastery of these relations helps students connect theoretical laws with real-life mechanical situations and perform well in examinations.
1. Equilibrium of a Particle (First Law):
For a particle in equilibrium:
$
\sum \vec{F}_{\text {net }}=0
$
or, in components:
$
\sum F_x=0, \quad \sum F_y=0, \quad \sum F_z=0
$
2. Lami's Theorem:
For three coplanar, concurrent, non-collinear forces in equilibrium:
$
\frac{F_1}{\sin \alpha}=\frac{F_2}{\sin \beta}=\frac{F_3}{\sin \gamma}
$
3. Force and Momentum:
- Linear momentum:
$
\vec{p}=m \vec{v}
$
- Newton's Second Law:
$
\vec{F}=\frac{d \vec{p}}{d t}
$
- For constant mass:
$
\vec{F}=m \vec{a}
$
4. Impulse:
- Impulse:
$
\vec{J}=\vec{F} \Delta t
$
- Relation with momentum:
$
\vec{J}=\Delta \vec{p}
$
5. Law of Conservation of Linear Momentum:
$\sum \vec{p}_{\text {initial }}=\sum \vec{p}_{\text {final }}$
6. Motion on a Rough Inclined Plane:
- Component of weight along the plane:
$
m g \sin \theta
$
- Normal reaction:
$
N=m g \cos \theta
$
7. Pseudo Force (Non-Inertial Frame):
$\vec{F}_p=-m \vec{a}$
8. Centripetal Force:
$
F_c=m \omega^2 r
$
The force that keeps a body moving in a circular path towards the centre
9. Kinetic Friction Force:
$
f_k=\mu_k R
$
Opposes relative motion between surfaces
10. Limiting (Maximum) Static Friction:
$
f_{\ell}=\mu_s R
$
Maximum static friction before motion begins
Laws of Motion: Previous Year Questions
Previous year questions from the chapter Laws of Motion mainly focus on the application of Newton’s laws, free body diagrams, friction, and conservation of momentum. These questions help students understand the exam pattern and identify frequently tested concepts and formulas. Practising them improves problem-solving skills and confidence in handling numerical problems. This section is highly useful for effective revision and exam-oriented preparation.
Question 1:
A body of mass 10 kg is acted upon by two perpendicular forces, 6 N and 8 N. The resultant acceleration of the body is
(a) $1 \mathrm{~ms}^{-2}$ at an angle of $\tan ^{-1}\left(\frac{4}{3}\right)$ w.r.t. 6 N force.
(b) $0.2 \mathrm{~m}_{\mathrm{s}^{-2}}$ at an angle of $\tan ^{-1}\left(\frac{4}{3}\right)$ w.r.t. 6 N force.
(c) $1 \mathrm{~m}_{s^{-2}}$ at an angle of $\tan ^{-1}\left(\frac{3}{4}\right)$ w.r.t. 8 N force.
(d) $0.2 \mathrm{~m}_{s^{-2}}$ at an angle of $\tan ^{-1}\left(\frac{3}{4}\right)$ w.r.t. 8 N force.
Solution:
Here we know that,
$
\mathrm{m}=10 \mathrm{~kg}, \mathrm{~F}_2=8 \mathrm{~N} \& \mathrm{~F}_1=6 \mathrm{~N}
$
$
R=\sqrt{8^2+6^2}
$
$
R=\sqrt{64+36}
$
$
R=\sqrt{100}
$
Thus, $\mathrm{R}=10 \mathrm{~N}$
$
F=m a \rightarrow a=\frac{F}{m}=\frac{R}{m}=\frac{10}{10}=1 \mathrm{~ms}^{-2}
$
$\tan \theta_1=\frac{8}{6}=\frac{4}{3}=\theta_1=\tan ^{-1}\left(\frac{4}{3}\right)$ $\qquad$
$\tan \theta_2=\frac{6}{8}=\frac{3}{4}=\theta_2=\tan ^{-1}\left(\frac{3}{4}\right)$
Hence, statement (a) is verified from (i) and (ii), whereas statement (c) is verified from (i) and (iii).
Since, acceleration is not equal to $0.2 \mathrm{~ms}^{-2}$, statements (b) & (d) are rejected.
Question 2:
Two billiard balls $A$ and $B$, each of mass 50 g and moving in opposite directions with a speed of 5 m s-1 each, collide and rebound with the same speed. If the collision lasts for $10^{-3} s$, which of the following statements are true?
(a) The impulse imparted to each ball is $0.25 \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1}$ and the force on each ball is 250 N.
(b) The impulse imparted to each ball is $0.25 \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1}$ and the force exerted on each ball is $25 \times 10^{-5} \mathrm{~N}$.
(c) The impulse imparted to each ball is 0.5 Ns.
(d) The impulse and the force on each ball are equal in magnitude and opposite in direction.
Solution:
(c) The impulse imparted to each ball is 0.5 Ns.
(d) The impulse and force on each ball are equal in magnitude and opposite in direction.
Let m be the mass of each ball, $\mathrm{m}=0.05 \mathrm{~kg}$
Let $v$ be the speed of each ball, $v=5 \mathrm{~m} / \mathrm{s}$
We know that the initial momentum of each ball will be
$
\begin{aligned}
& \overrightarrow{p_i}=m \vec{v} \\
& \overrightarrow{p_i}=(0.05)(5)=0.25 \mathrm{kgms}^{-1} \\
& =0.25 \mathrm{~N}-\mathrm{s}
\end{aligned}
$
After the collision, on rebounding, the direction of the velocity of each ball is reversed; hence, the final momentum of each ball will be
$
\begin{aligned}
& \vec{p}=m(-\vec{v}) \\
& =-0.25 \mathrm{~N}-\mathrm{s} .
\end{aligned}
$
Hence, statement (d) is verified.
Thus, it is clear that the impulse imparted to each ball is equal to the change in momentum of each ball
$
\begin{aligned}
& =p_f-p_i \\
& =-0.25-(0.25) \\
& =-0.50 \mathrm{~kg} \mathrm{~ms}^{-1} \\
& =-0.50 \mathrm{~N}-\mathrm{s}
\end{aligned}
$
Here, statement (c) is also verified.
Question 3:
In the figure, the coefficient of friction between the floor and the body B is 0.1. The coefficient of friction between the bodies $B$ and $A$ is 0.2. A force $F$ is applied as shown on $B$. The mass of $A$ is $\frac{m}{2}$ and of $B$ is $m$. Which of the following statements are true?
(a) The bodies will move together if F = 0.25 mg.
(b) The body A will slip with respect to B if F = 0.5 mg.
(c) The bodies will move together if F = 0.5 mg.
(d) The bodies will be at rest if F = 0.1 mg.
(e) The maximum value of F for which the two bodies will move together is 0.45 mg.
Solution:
Consider the adjacent diagram. The frictional force on $B\left(f_1\right)$ and the frictional force on $A\left(f_2\right)$ will be as shown.
Lat A and B are moving together $a_{\text {common }}=\frac{F-t_1}{m_A+m_B}$
$
\begin{aligned}
& =\frac{F-f_1}{\left(\frac{m}{2}\right)+m} \\
& =\frac{2\left(F-f_1\right)}{3 m}
\end{aligned}
$
Pseudo force on $A=\left(m_A\right) \times a_{\text {common }}$
$
\begin{aligned}
& =m_A \times \frac{2\left(F-f_1\right)}{3 m} \\
& =\frac{m}{2} \times \frac{2\left(F-f_1\right)}{3 m} \\
& =\left(F-f_1\right) \frac{)}{3}
\end{aligned}
$
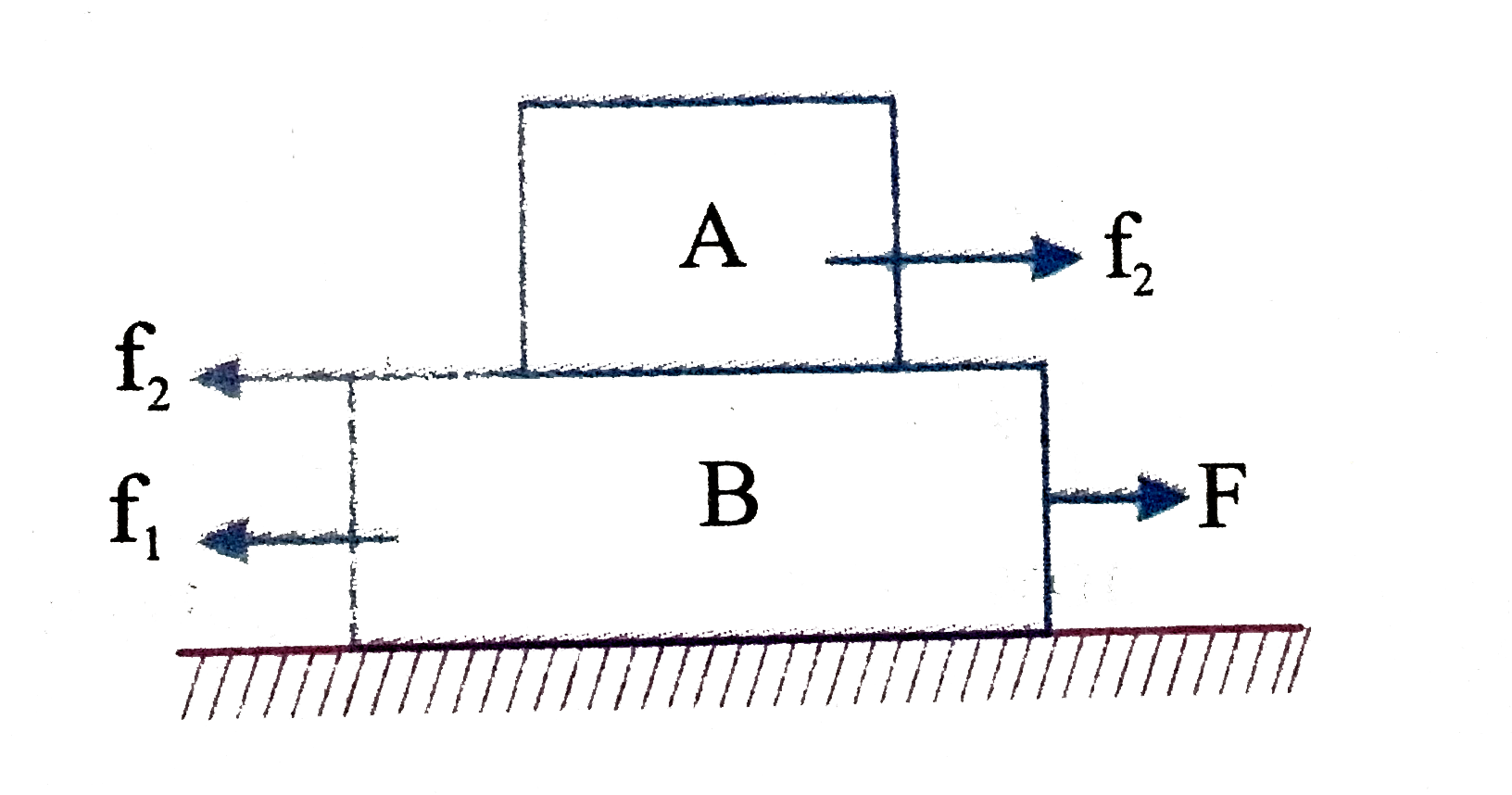
The force $(\mathrm{F})$ will be maximum when
Pseudo force on $\mathrm{A}=$ Frictional force on A
$
\begin{aligned}
& \Rightarrow \frac{F_{\max }-f_1}{3}=\mu m_A g \\
& =0.2 \times \frac{m}{2} \times g \\
& =0.1 \mathrm{mg} \\
& \Rightarrow F_{\max }=0.3 m g+f_1 \\
& =0.3 m g+(0.1) \frac{3}{2} m g \\
& =0.45 \mathrm{mg}
\end{aligned}
$
⇒ Hence, the maximum force up to which bodies are together is $F_{\max }=0.45 m g$
a. Hence, for $\mathrm{F}=0.25 \mathrm{mg}<\mathrm{F}_{\max }$ bodies will move together.
b. For $\mathrm{F}=0.5 \mathrm{mg}>\mathrm{F}_{\max }$, body A will slip with respect to B .
c. For $\mathrm{F}=0.5 \mathrm{mg}>\mathrm{F}_{\max }$, bodies slip.
$
\begin{aligned}
& \left(f_1\right)_{\max }=\mu m_B g=(0.1) \times \frac{3}{2} m \times g=0.15 \mathrm{mg} \\
& \left(f_2\right)_{\max }=\mu m_A g=(0.2)\left(\frac{m}{g}\right) g=0.1 \mathrm{mg}
\end{aligned}
$
Hence, the minimum force required for the moment of the system ( $\mathrm{A}+\mathrm{B}$ )
$
\begin{aligned}
& F_{\min }=\left(f_1\right)_{\max }+\left(f_2\right)_{\max } \\
& =0.15 \mathrm{mg}+0.1 \mathrm{mg} \\
& =0.25 \mathrm{mg}
\end{aligned}
$
d. Given, force $\mathrm{F}=0.1 \mathrm{mg}<\mathrm{F}_{\min }$.
Hence, the bodies will be at rest.
e. Maximum force for combined movement $\mathrm{F}_{\max }=0.45 \mathrm{mg}$.
Laws of Motion in Different Exams
The chapter Laws of Motion is an important and high-weightage topic across various examinations due to its fundamental role in mechanics and problem-solving. This chapter is evaluated by the various exams with conceptual questions, numerical questions, and application-based questions that involve forces and motion. The clarity in terms of Newton's laws, free body diagrams, friction and momentum enables the students to tackle the questions of different degrees of difficulty. This topic is applicable in school tests and in competitive tests, hence a good grounding in mechanics is necessary.
| Exam | Focus Areas | Common Questions Asked | Marks / Questions Weightage | Preparation Tips |
|---|---|---|---|---|
| JEE Main | Newton’s laws, friction, and momentum | Numerical MCQs, FBD-based problems | 1–2 questions (4–8 marks) | Strong grip on formulas, practice numericals |
| JEE Advanced | Multi-body systems, friction, momentum conservation | Conceptual + multi-step numerical problems | 1 question (variable marks) | Focus on concepts, not rote learning |
| NEET | Newton’s laws, friction, and basic momentum | Direct formula-based MCQs | 1–2 questions (4–8 marks) | Memorise formulas and NCERT examples |
| UPSC CDS / NDA | Basics of force and motion | One-liners, simple numericals | 1 question (2–4 marks) | Revise definitions and standard results |
| State-Level Exams (WBJEE, MHT-CET, etc.) | Friction, Newton’s laws, FBDs | Conceptual + numerical MCQs | 1–2 questions (4–8 marks) | Practice PYQs and speed-based questions |
| GATE | Fundamentals of Newtonian mechanics | Conceptual questions (limited) | Low/rare | Focus on core principles |
| School-Level (CBSE, ICSE, State Boards) | Entire chapter | Numericals, derivations, FBDs | 6–8 marks | Master the NCERT theory and diagrams |
| CUET | Conceptual understanding | MCQs, assertion–reason | 1–2 questions (4–6 marks) | Focus on basic laws and applications |
| SSC & Banking Exams | Basic mechanics facts | One-liners, matching type | 1 question (1–2 marks) | Revise key definitions and applications |
Important Books and Resources for Class 11 Laws of Motion
The best way to study the chapter Laws of Motion is to consult good textbooks, reference books and problem-solving books, which demonstrate the fundamentals and problem-solving procedures that involve the forces, motion, friction, and momentum. These books assist in developing a great level of conceptual clarity and mathematical abilities that are required in board exams and competitive exams such as JEE Main, JEE Advanced and NEET.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Class 11 Physics (Part I) | NCERT | The official textbook covers all foundational topics such as Newton’s laws, inertia, friction, momentum, and equilibrium with clear explanations and examples. |
| NCERT Exemplar Physics (Class 11) | NCERT | Offers higher-order and application-based questions on Newton’s laws, friction, and momentum for deeper conceptual practice. |
| Concepts of Physics – Volume 1 | H.C. Verma | Excellent for strengthening fundamentals and solving challenging problems related to forces, motion, and dynamics. |
| Understanding Physics: Mechanics | D.C. Pandey (Arihant) | Detailed topic-wise explanations, solved examples, and practice questions focused on laws of motion, friction, and momentum. |
| Physics for Class 11 | R.D. Sharma | Step-by-step theory with a wide variety of solved and unsolved problems on Newton’s laws and related applications. |
| Arihant All-In-One Physics (Class 11) | Arihant | Comprehensive guide with concise theory summaries, solved examples, and practice questions, including past exam problems on laws of motion. |
| MTG Chapter-wise Previous Year Questions – Physics | MTG | Helps students practice and analyse past questions specifically from the Laws of Motion chapter across board and competitive exams. |
NCERT Resources for Laws of Motion
NCERT resources for the chapter Laws of Motion provide a clear and structured explanation of force, motion, and their interrelationships. The textbook has the laws of Newton, friction, momentum, and equilibrium expressed in a straightforward language, diagrams, and illustrations. The exercises of NCERT, examples, and solved problems contribute to students having a good conceptual clarity and numerical-solving abilities. These are the resources on which the board exam preparation and competitive examinations are based.
NCERT Subject-Wise Resources
NCERT subject-wise materials are organised and syllabus-based learning content on various subjects, which assists students in developing a good conceptual basis. They consist of textbooks, exemplar problems, and solutions and can thus be very helpful in the preparation for the board exams and even competitive exams such as JEE and NEET.
Practice Questions based on Laws of Motion
Practice questions from the chapter Laws of Motion help students strengthen their understanding of the relationship between force and motion. These questions revolve around the use of Newton laws, free body diagrams, friction as well as conservation of momentum. The practice enhances the speed, accuracy, and confidence towards the numerical calculations. Such questions are also important in solving tests that are required when doing well in school examinations and also in competitive exams.
Conclusion
The chapter Laws of Motion gives a good conceptual basis to the relationship between force and motion in mechanics. Students can acquire good analysis and problem-solving skills by consistently updating the laws of Newton, the use of free body diagrams, the use of important formulas and concepts of friction and momentum. The methodical and consistent approach to practice can contribute to the development of confidence and precision in calculating problems. It is a very successful preparation for taking exams in Class 11 and also competitive exams like JEE Main and NEET.
Frequently Asked Questions (FAQs)
It is known as the Law of Inertia.
It simply states that for every action there is an equal and opposite reaction.
Firing a bullet
Rocket Propulsion
Rowing a boat
Recall of a gun
Pushing a wall
Newton (N) is the unit of force. It is the force needed to accelerate 1kg of mass at the rate of one metre per second squared.
The newton’s second law of motion is called the real law because both the first and third laws of motion can be derived using the second law.
