Lens Displacement Method

The lens displacement method is a practical technique used to determine the focal length and optical properties of lenses by analyzing how the position of an image changes when the lens is displaced. This method involves measuring the displacement of the lens and the resulting shift in the image position to calculate key optical parameters. In real life, the lens displacement method is crucial in the design and calibration of optical instruments such as cameras, microscopes, and telescopes, where precise lens placement and focusing are essential. For example, in camera systems, understanding lens displacement helps in adjusting focus and achieving sharp images. This technique is also employed in quality control and testing of lenses in various optical devices, ensuring optimal performance and accurate image formation. In this article, we will explore the principles of the lens displacement method, its formulas, and practical examples to illustrate its applications and significance.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

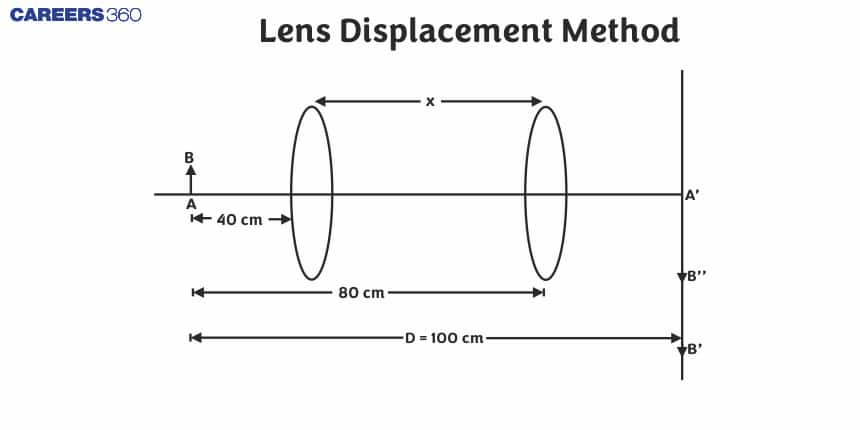
Displacement Method

The displacement method is an optical technique used to determine the focal length of a lens by measuring how the image position shifts as the lens is displaced. This method is based on the principle that the change in the image position is related to the displacement of the lens and the lens’s focal length. This method helps us to find the other position of the object which causes the sharp image on the screen.

For this let us consider a convex lens L placed between an object O and a screen S. If the distance between the object and the screen is D and the positions of the object and the screen are held fixed. The lens is allowed to move along the axis of the system and at a position 'I' a sharp image will be formed on the screen. Interestingly, there is another position on the same axis where a sharp image will once again be obtained on the screen. See in the figure given below that the second position is 'II'

In the figure, let the distance of position I from the object be x1. Then, the distance of the screen from the lens is D−x1. Therefore, u=−x1 and v=+(D−x1)

Substituting in the lens equation

1v−1u=1f⇒1D−x1+1x1=1f…

At position II, let the distance of the lens from the screen be x2. Then, the distance of the lens from the object is D−x2. Therefore, u=−x2 and v=+(D−x2).

Now substituting in lens formula

1D−x2+1x2=1f…(2)

Comparing (1) and (2), we get
1. x1=x2; or
2. D−x1=x2 and D−x2=x1

The first solution is trivial. Therefore, if the first position of the lens, for a sharp image, is x1 from the object, the second position is at D−x1 from the object. Let the distance between the two positions I and If be d. From the diagram, it is clear that

D=x1+x2 and d=x2−x1

Solving the two equations in (iii), we obtain
x1=D−d2 and D−x1=D+d2…(iv)$

Substituting Eq. (iv) in Eq. (i), we get
1f=2D−d+2D+df=D2−d24D…(v)

Also, d=D2−4Df=D(D−4f).

We notice from Eq. (v) that a solution for d is possible only when D≥4f.
When D<4f, there is no position for which a sharp image can be formed.
When D=2f, there is only one position where a sharp image is formed.
When D>2f, there are two positions where a sharp image is formed.

Note - This method is applicable to convex lens, not for concave lens

Solved Examples Based on Lens Displacement Method

Example 1: A screen is kept at a distance of 1 m from the object. A converging lens between the object and screen when placed at any positions which are 60cm apart forms a sharp image of the object on the screen, The focal length of the lens is:

1) 8cm

2) 12cm

3) 14cm

4) 16cm

Solution:

d= Distance between two positions of a convex lens.
D= Distance between object and screen
$$
f=\frac{D^2-d^2}{4 D}
whereDisthedistancebetweentheobjectandthescreenandd$ is the distance between the two positions of lenses for which sharp images of the given object are obtained on the screen.

Here D=1 m=100 cm d=60 cm
f=1002−6024×100=16 cm

Hence, the answer is the option (4).

Example 2: The minimum distance between the object and the screen to form a real image by a converging lens is:

1) f

2) 2f

3) 3f

4) 4f

Solution:

Condition of formation of the real image
D≥4f
wherein
Distance between object \& screen should be greater than or equal to 4f focal length
d=D(D−4f)
for d to be real, D−4f⩾0
D>4f

Hence, the answer is the option (4)

Summary

The lens displacement method is a technique for determining the focal length of a lens by measuring the shift in image position when the lens is displaced. This method is valuable in calibrating optical instruments like cameras, microscopes, and telescopes, ensuring precise focusing and image clarity. By analyzing how the image position changes with lens displacement, the focal length can be accurately calculated, which is crucial for achieving optimal performance in various optical applications.