Magnetic Force - Definition, Formula, Magnetic Force on a Current-Carrying Conductor, FAQs

Edited By Vishal kumar | Updated on Nov 25, 2024 05:07 PM IST

The magnetic force is an outcome of the electromagnetic force. This magnetic force is caused by the movement of charged particles. The magnetic force is a force that is produced by magnetic field interactions. In this article, we will discuss what is magnetic force, the magnetic force formula, features of interaction between electric field and magnetic field, right hand thumb rule, Coulomb's law for magnetic force, magnetic force on a current-carrying conductor class 12, magnetic force examples, and moving charges and magnetism formulas.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

What is Magnetic Force
Magnetic Force Formula
Features of Interaction Between Electric Field and Magnetic Field
Coulomb's Law for Magnetic Force
Magnetic Force on a Current-Carrying Conductor Class 12
Magnetic Force Examples
Moving Charges and Magnetism Formulas

Magnetic Force - Definition, Formula, Magnetic Force on a Current-Carrying Conductor, FAQs

What is Magnetic Force

Consider a point charge ‘$q$’ placed in both magnetic and electric fields. The magnitude of the magnetic field is given by $B$ and the magnitude of the electric field is given by $4E$. The total force on the charge $q$ is given as the summation of both electric and magnetic force that acts on the charge i.e. $F_E+F_M$, where $F_E$ is the electric force and $F_M$ is the magnetic force.

The definition of magnetic force can be written as:

The magnetic force is the force of attraction or repulsion that acts between two accelerated charged particles which are exerted on one charge by the magnetic field produced by the other charged particle.

Magnetic Force Formula

The value of the magnitude of the magnetic force relies on the amount of charge that is in motion and the distance between them. The mathematical expression of the magnetic force can be written as,

$$\mathbf{F}=q[\mathbf{E}(\mathbf{r})+\mathbf{v} \times \mathbf{B}(\mathbf{r})]$$

where,

$F$ is the total force acting on the charged particle
$q$ charge of the particle
$E(r)$ is the electric field vector at position r
$v$ is the velocity vector of the particle
$B(r)$ is the magnetic field vector at position r

This magnetic force is known as the ‘Lorentz Force’. It describes the force which is known as the combined electric and magnetic force of a point charge q which is caused due to EM fields.

Features of Interaction Between Electric Field and Magnetic Field

The features of the interaction of Electric and Magnetic fields are discussed below:

The magnetic force is a dependent quantity. It depends on the charge q of the accelerated particle, velocity v of the particle, and magnetic field B.
The magnetic force direction is opposite to the direction of the positive charge i.e. in the direction of the negative charge.
The cross product or vector representation of the velocity v of the particle and the magnetic field B gives the magnitude of the magnetic force in the vector form. Also, the cross product can be replaced with $\sin \theta$and the expression is written as $\mathrm{F}=\mathrm{qvB} \sin \theta$, where $\theta$ denotes the angle between the velocity component and the magnetic field component. And this $\theta$ is found to be less than 180 degrees.
The resultant force stands normal to the velocity and magnetic field direction. The direction of the magnetic field is calculated by the right-hand thumbs rule or right-hand slap rule.
The total magnetic force becomes zero for static charges, that is, the magnetic force is found only in moving charges. Also, the magnetic force of the charged particle moving in a parallel direction to the magnetic field is zero.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Right-Hand Thumb Rule

If the current-flowing conductor is held by the right hand, the direction facing the thumb gives the direction of the flow of electric current and the direction of other curled fingers gives the direction of the magnetic field carried by the current-carrying conductor.

Related Topics,

Coulomb's Law for Magnetic Force

Coulomb's law for magnetic force tells that the magnetic force between any two poles in a magnetic medium should have direct proportionality with their pole strength and inversely proportional to the absolute permeability and the square of the distance between the two poles. The mathematical expression for this law is given as

$$
\begin{gathered}
F \propto \frac{m_1 m_2}{\mu_0 r^2} \\
F=k \frac{m_1 m_2}{\mu_0 r^2}
\end{gathered}
$$

Where

$m_1$ and $m_2$ stands for their pole strength
$r$ is the distance between the poles,
$\mu_0$ is the absolute permeability
$k$ is the constant proportionality.

Magnetic Force on a Current-Carrying Conductor Class 12

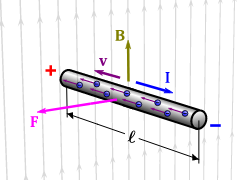
The resultant force stands normal to the velocity and magnetic field direction. The direction of the magnetic field is calculated by the right hand thumbs rule.

The magnetic force will be produced by the magnetic field in a straight long current-carrying conductor. Consider the length of the conductor to be l and the area of the cross-section to be A. Let the n number density of the electrons. When the conductor is placed in some external magnetic field B,

Magnetic force on a moving charge:

$
\mathbf{F}=q \mathbf{v} \times \mathbf{B}
$

The current in the conductor will be given as

$
I=n q v_d A
$

Where

$n$ is charge carrier density
$q$ is the charge
$v_d$ is the drift velocity
$A$ is the cross-sectional area

The force for a small length $d \mathbf{l}$ of the conductor is

$$
d \mathbf{F}=q\left(\mathbf{v}_d \times \mathbf{B}\right) \cdot n A d \mathbf{l}
$$

The magnitude of the magnetic force due to a current-carrying conductor is

$$
F=I L B \sin \theta
$$

Magnetic Force Examples

Aurora Borealis, the northern lights is an example of magnetic force in moving charges.
Magnetic levitation trains are an example of magnetic force on a current-carrying conductor.
The compass needle is an example of magnetic force on magnetic materials.
Magnetic force is used in Cyclotron and mass spectrometers.
Loudspeakers and electric bells are the everyday applications of magnetic forces.

Moving Charges and Magnetism Formulas

The important topics and their formulas related to the concept of moving charges and magnetism are given in the table below:

Concept	Formula
Lorentz Force	$\mathbf{F}=q(\mathbf{E}+\mathbf{v} \times \mathbf{B})$
Magnetic Force on a Moving Charge	$\mathbf{F}=q(\mathbf{v} \times \mathbf{B})$
Magnetic Force on a Current-Carrying Conductor	$\mathbf{F}=I \mathbf{L} \times \mathbf{B}$
Magnitude of Magnetic Force	$F=q v B \sin \theta$
Magnetic Field of a Long Straight Current-Carrying Wire	$B=\frac{\mu_0 I}{2 \pi r}$
Magnetic Field at the Center of a Circular Loop	$B=\frac{\mu_0 I}{2 R}$
Ampere’s Circuital Law	$\oint \mathbf{B} \cdot d \mathbf{l}=\mu_0 I_{\mathrm{enc}}$
Biot-Savart Law	$d \mathbf{B}=\frac{\mu_0}{4 \pi} \frac{I d \mathbf{l} \times \hat{r}}{r^2}$
Force Between Two Parallel Current-Carrying Wires	$F=\frac{\mu_0 I_1 I_2 L}{2 \pi r}$
Cyclotron Radius	$r=\frac{m v}{q B}$
Cyclotron Time Period	$T=\frac{2 \pi m}{q B}$
Magnetic Moment of a Current Loop	$M=I A$
Torque on a Current Loop	$\tau=\mathbf{M} \times \mathbf{B}$
Potential Energy of a Magnetic Dipole	$U=-\mathbf{M} \cdot \mathbf{B}$

Also read:

Frequently Asked Questions (FAQs)

1. What is a magnetic force or give the magnetic force definition:

2. Give some magnetic force examples:

Some of the components that work with the help of the magnetic force are a compass, MRI scanner, speaker, electric motor, computer and so on.

3. What is the magnetic force formula or write down the mathematical expression for magnetic force:

The cross product or vector representation of the velocity v of the particle and the magnetic field B gives the magnitude of the magnetic force is given in the vector form and the relation is F=q[v✖B]. Also, the cross product can be replaced with sinθ and the expression is written as F=qvBsinθ, where θ denotes the angle between the velocity component and the magnetic field component. And this θ is found to be less than 180 degrees.

4. Is the magnetic field a scalar quantity?

The magnetic field is not a scalar quantity. As it contains both magnitude and direction of its own, the magnetic field is defined to be a vector quantity.

5. What is the law of magnetic force?