Malus's Law

Malus's Law describes the intensity of polarized light transmitted through an analyzer as a function of the angle between the light's initial polarization direction and the analyzer's axis. This fundamental principle in optics helps us understand how light behaves when it passes through polarizing filters. In real life, Malus's Law is applied in various technologies, such as polarized sunglasses, which reduce glare by blocking certain light waves, and in liquid crystal displays (LCDs) used in screens, where controlled polarization is key to image clarity. By grasping Malus's Law, we can appreciate the behaviour of polarized light and its practical applications in improving visual comfort and display technology. In this article, we will discuss the concept of Malus' Law and provide examples for better clarity.

This Story also Contains

1. Malus' Law
2. Solved Examples Based on Malus' Law
3. Summary

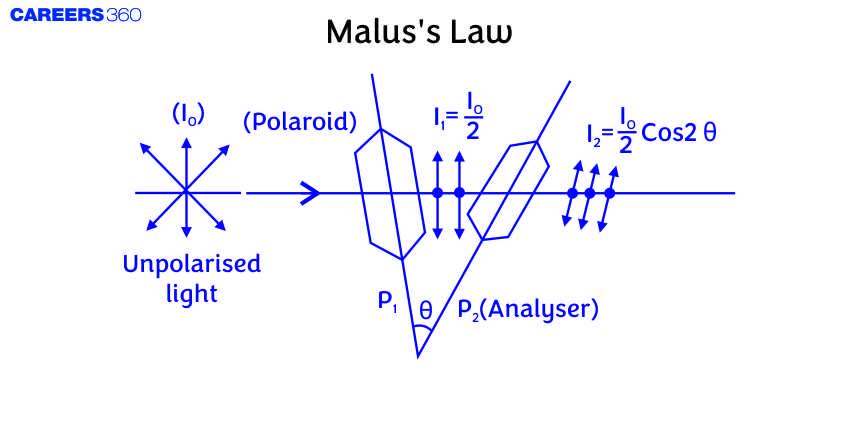
Malus' Law

Malus' Law describes the intensity of polarized light passing through a polarizing filter as a function of the angle between the light's initial polarization direction and the axis of the filter. Formulated by Étienne-Louis Malus in 1809, the law states that the transmitted light intensity is proportional to the square of the cosine of the angle between the initial polarization direction and the filter's axis. This principle is fundamental in optics, helping to explain and predict the behaviour of polarized light in various scenarios.

This law states that the intensity of the polarized light transmitted through the analyzer varies as the square of the cosine of the angle between the plane of transmission of the analyzer and the plane of the polarizer.

As,

$
I=I_0 \cos ^2 \theta \text { and } A^2=A_0^2 \cos ^2 \theta \Rightarrow A=A_0 \cos \theta
$

If $\theta=0^{\circ}, I=I_0, A=A_0$, and if $\theta=90^{\circ}, I=0, A=0$

If I_i = Intensity of unpolarised light. So

$I_0=\frac{I_i}{2}$

i.e. if an unpolarized light is converted into plane polarised light (say by passing it through a Polaroid or a Nicol-prism), its intensity becomes half and

$I=\frac{I_i}{2} \cos ^2 \theta$

Recommended Topic Video

Solved Examples Based on Malus' Law

Example 1: Unpolarized light of intensity I pass through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be I/2. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be I/8. The angle between polarizers A and C is :

1) 60^o

2) 0^o

3) 30^o

4) 45^o

Solution:

Malus Law

$
I=I_0 \cdot \cos ^2 \theta
$
$\theta=$ angle made by E vector with transmission axis.
wherein
$I=$ Intensity of transmitted light after polarisation.
$I_0=$ intensity of incident light.

$\begin{aligned} & \because \frac{I}{2} \cos ^4 \theta=\frac{I}{8} \\ & \text { or } \cos ^4 \theta=\frac{1}{4} \\ & \therefore \cos \theta=\frac{1}{\sqrt{2}} \\ & \text { or } \theta=45^{\circ}\end{aligned}$

Hence the answer is the option (4).

Example 2: A system of three polarizers $P_1, P_2, P_3$ is set up such that the pass axis of $P_3$ is crossed with respect to that of $P_1$. The pass axis of $P_2$ is inclined at $60^{\circ}$ to the pass axis of $P_{3 .}$. When a beam of unpolarized light of intensity $I_o$ is incident on $P_1$, the intensity of light transmitted by the three polarizers is I. The ratio $\left(I_o / I\right)$ equal (nearly):

1) 5.33

2) 16.00

3) 10.67

4) 1.80

Solution:

$
I=I_0 \cdot \cos ^2 \theta
$
$\theta=$ angle made by an E vector with a transmission axis.
wherein I the Intensity of transmitted light after polarization.
$I_0=$ Intensity of incident light.
the intensity of light transmitted from
$
P_1=\frac{I_o}{2}
$
the intensity of light transmitted from
$
P_2=\frac{I_o}{2} \cos ^2 30=\frac{3 I_o}{8}
$

The intensity of light transmitted from $P_3$
$
\begin{aligned}
& I=\frac{3 I_o \cos ^2 60}{8}=\frac{3 I_o}{32} \\
& \frac{I_o}{I}=\frac{32}{3}=10.67
\end{aligned}
$

Hence the answer is the option (3).

Example 3: A polarizer-analyzer set is adjusted such that the intensity of light coming out of the analyzer is just 10% of the original intensity. Assuming that the polarizer-analyzer set does not absorb any light, the angle by which the analyzer needs to be rotated further to reduce the output intensity to be zero is:

1) 71.6^o

2) 90^o

3) 18.4^o

4) 45^o

Solution:

Malus's Law states that the intensity of the polarized light transmitted through the analyzer varies as the square of the cosine of the angle between the plane of transmission of the analyzer and the plane of the polarizer.

As,

$
I=I_0 \cos ^2 \theta
$
output intensity is given by $I=I_0 \operatorname{Cos}^2(\theta)$
Initial output intensity $=10 \%$ of $\mathrm{I}_0$
$
\text { I.e } \frac{10 I_0}{100}=I_0 \operatorname{Cos}^2(\theta) \Rightarrow \theta=71.57
$

Final output intensity $=\mathrm{O}$
means a new angle is $90^{\circ}$
the angle by which the analyser needs to be rotated further is $90^{\circ}-\theta=18.4^{\circ}$

Hence the answer is the option (3).

Example 4: A beam of plane polarised light of a large cross-sectional area of the uniform intensity of 3.3 Wm^-2 falls normally on a polariser (cross-sectional area ) which rotates about its axis with an angular speed of 31.4 rad/s. The energy of light passing through the polariser per revolution is close to:

1) $1.1 \times 10^{-5} \mathrm{~J}$
2) $1.0 \times 10^{-4} \mathrm{~J}$
3) $1.5 \times 10^{-4} \mathrm{~J}$
4) $5.0 \times 10^{-4} \mathrm{~J}$

Solution:

Given
$
\begin{aligned}
& \text { Intensity, } I=3.3 \mathrm{Wm}^{-2} \\
& \text { Area }=A=3 \times 10^{-4} \mathrm{~m}^2 \\
& \text { Angular speed }=\omega=31.4 \mathrm{rad} / \mathrm{s}
\end{aligned}
$

Intensity, $I=3.3 \mathrm{Wm}^{-2}$
Area $=A=3 \times 10^{-4} \mathrm{~m}^2$
Angular speed $=\omega=31.4 \mathrm{rad} / \mathrm{s}$
now as we know $<\cos ^2 \theta>=\frac{1}{2}$, in one time period
$
\therefore \text { Average energy }=\mathrm{I}_0 \mathrm{~A} \times \frac{1}{2}=\frac{(3.3)\left(3 \times 10^{-4}\right)}{2} \simeq 5 \times 10^{-4} \mathrm{~J}
$

Hence the answer is the option (4).

Example 5: An unpolarized light beam is incident on the polarizer of the polarization experiment and the intensity of the light beam emerging from the analyser is measured as 100 Lumens. Now, if the analyzer is rotated around the horizontal axis (direction of light) the intensity of emerging light will be ________ Lumens.

1) 75

2) 50

3) 25

4) 15

Solution:

Assuming the initial axis of the Polarizer and Analyzer are parallel

Now emerging intensity $=\frac{\mathrm{I}_0}{2} \cos ^2 30^{\circ}=100\left(\frac{\sqrt{3}}{2}\right)^2=100 \times \frac{3}{4}=75$

Summary

Malus's Law explains how the intensity of polarized light varies when passing through an analyzer, depending on the angle between the light's polarization direction and the analyzer's axis. This principle is fundamental in understanding the behaviour of polarized light, with applications in technologies like polarized sunglasses and LCD screens. By studying examples and solving problems based on Malus's Law, one gains a deeper appreciation for its significance in practical optics and its role in enhancing visual clarity and comfort in everyday devices.