Mayer's Formula

Mayer's Formula

Edited By Vishal kumar | Updated on Nov 17, 2024 10:20 AM IST

Mayer's formula explains the relationship between the specific heat of gas at constant pressure and constant volume, which is one of the most essential equations in thermodynamics. According to it, gas constant (R) is the difference between specific heat at constant pressure (Cp) and specific heat at constant volume (Cv). Thus, this makes it possible to understand better how energy flows take place in gases and how their heat capacity changes depending on the circumstances.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

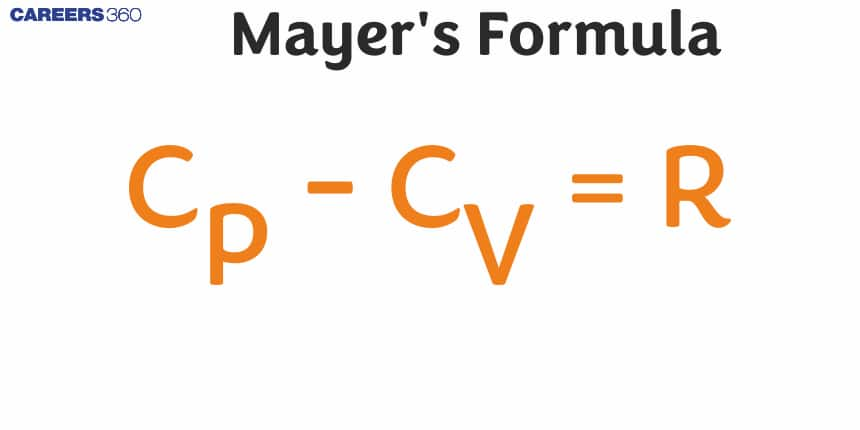
Mayer's Formula

In this article, we will cover the concept of the 'Mayer's Formula’. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), seventeen questions have been asked on this concept. And for NEET two questions were asked from this concept.

Let's read this entire article to gain an in-depth understanding of Mayer's Formula.

Molar Specific heat of the gas at constant volume $= C_{v}$
and Molar-specific heat capacity at constant pressure $C_{p}$
Mayer's formula gives the relation between $C_{p}$ and $C_{v}$ as $C_{p} = C_{v} + R$

or we can say that molar Mayer’s formula shows that specific heat at constant pressure is greater than that at constant volume.

Specific Heat in Terms of Degree of Freedom

1. Molar Specific heat of the gas at constant volume ( $C_v$ )

For a gas at temperature T, the internal energy

$U = \frac{f}{2} n R T \Rightarrow Change in energy Δ U = \frac{f}{2} n R Δ T \dots$

Also, as we know any gas heat supplied at a constant volume

$(Δ Q)_{V} = n C_{V} Δ T = Δ U \dots \dots (ii)$

From the equation (i) and (ii)

$C_{v} = \frac{f R}{2}$

where

f = degree of freedom

R= Universal gas constant

Molar Specific heat of the gas at constant pressure ( $C_p$ )

From Mayer's formula, we know that $C_{p} = C_{v} + R$
$\Rightarrow C_{P} = C_{V} + R = \frac{f}{2} R + R = (\frac{f}{2} + 1) R$

Atomicity or adiabatic coefficient ( $\gamma$ )

It is the ratio of $C_{p}$ to $C_{v}$
$γ = \frac{C_{p}}{C_{v}} = 1 + \frac{2}{f}$

$Value of γ is always more than 1$

$for Monoatomic gas γ = \frac{5}{3}$

for Diatomic gas $γ = \frac{7}{5}$

for Triatomic gas $γ = \frac{4}{3}$

What is a Gaseous Mixture?

If two non-reactive gases $A$ and $B$ are enclosed in a vessel of volume $V$ .
In the mixture $n_{1}$ mole of Gas $A$ (having Specific capacities as $C_{p 1}$ and $C_{v 1}$ , Degree of freedom $f_{1}$ and Molar mass as $M_{1}$ ) is mixed with
$n_{2}$ mole of Gas B (having Specific capacities as $C_{p 2}$ and $C_{v 2}$ ,Degree of freedom $f_{2}$ and Molar mass as $M_{2)}$

Then Specific heat of the mixture at constant volume will be

$C_{v_{mix}} = \frac{n_{1} C_{v_{1}} + n_{2} C_{v_{2}}}{n_{1} + n_{2}}$

Similarly, the Specific heat of the mixture at constant pressure will be

$C_{p_{mix}} = \frac{n_{1} C_{p_{1}} + n_{2} C_{p_{2}}}{n_{1} + n_{2}}$

And adiabatic coefficient ( $\gamma$ ) of the mixture is given by

$γ_{mixure} = \frac{C_{p_{mix}}}{C_{v_{m \in}}} = \frac{\frac{(n_{1} C_{p_{1}} + n_{2} C_{p_{2}})}{n_{1} + n_{2}}}{\frac{(n_{1} C_{v_{1}} + n_{2} C_{v_{2}})}{n_{1} + n_{2}}} = \frac{(n_{1} C_{p_{1}} + n_{2} C_{p_{2}})}{(n_{1} C_{v_{1}} + n_{2} C_{v_{2}})}$

Also

$\frac{1}{γ_{mix} - 1} = \frac{\frac{n_{1}}{γ_{1} - 1} + \frac{n_{2}}{γ_{2} - 1}}{n_{1} + n_{2}}$

Similarly, the Degree of freedom of mixture is given as
$f_{mix} = \frac{n_{1} f_{1} + n_{2} f_{2}}{n_{1} + n_{2}}$

Similarly, the molar mass of the mixture
$M_{m i x} = \frac{n_{1} M_{1} + n_{2} M_{2}}{n_{1} + n_{2}}$

Learn Mayer's Formula With a Video Lecture

Solved Examples Based on Mayer's Formula

Example 1: The specific heats $C_{p} and C_{v}$ of a gas of diatomic molecules A are given ( in units of $J\:mol^{-1}$ ) by 29 and 22 respectively. Another gas of diatomic molecule B has the corresponding values of 30 and 21 respectively. If they are treated as ideal gases then :

1) A is rigid but B has a vibrational mode.

2) A has a vibrational mode but B has none.

3) A has one vibrational mode and B has two.

4) Both A and B have a vibrational mode each.

Solution:

Specific heat capacity at constant pressure -

$\begin{aligned} C_{p} = C_{v} + R \\ = (\frac{f}{2} + 1) R \end{aligned}$
wherein
$f =$ degree of freedom
$R =$ Universal gas constant
$\frac{C_{p}}{C_{v}} = 1 + \frac{2}{f}$

For gas A,
$\begin{aligned} \frac{29}{22} = 1 + \frac{2}{f} \Rightarrow \frac{2}{f} = \frac{7}{22} \\ \Rightarrow f = \frac{44}{7} ≃ 6 \end{aligned}$

3 translations, 2 rotations, Remaining vibrational mode

For gas B,

$\begin{aligned} \frac{C_{p}}{C_{v}} = \frac{30}{21} = 1 + \frac{2}{f} \Rightarrow \frac{2}{f} = \frac{9}{21} \\ \Rightarrow f = \frac{42}{9} ≃ 5 \end{aligned}$

3 translations, 2 rotations, no vibrational mode

Hence, the answer is the option (2).

Example 2: Two moles of helium are mixed with n moles of hydrogen.

If $\frac{C_{p}}{C_{v}} = 3 / 2$ for the mixture, then the value of n is :

1) 1

2) 3

3) 2

4) 1.5

Solution:

As we have learned

Atomicity or adiabatic coefficient (gamma) -

$\begin{aligned} γ = \frac{C_{p}}{C_{v}} \\ = 1 + \frac{2}{f} \end{aligned}$
wherein
for Monoatomic gas
$γ = \frac{5}{3}$
for Diatomic gas
$γ = \frac{7}{5}$
for Triatomic gas
$γ = \frac{4}{3}$
$\begin{aligned} c_{p}^{mix} = \frac{n_{1} c p_{1} + n_{2} c p_{2}}{n_{1} + n_{2}} = \frac{2 * 5 R / 2 + n (7 R / 2)}{2 + n} = \frac{10 + 7 n}{2 + n} R \\ c_{v}^{mix} = \frac{n_{1} c v_{1} + n_{2} c v_{2}}{n_{1} + n_{2}} = \frac{2 * 3 R / 2 + n (5 R / 2)}{2 + n} = \frac{6 + 5 n}{2 + n} R \end{aligned}$

$r^{mix} = \frac{3}{2} = \frac{c_{p}^{mix}}{c_{v}^{mix}} = \frac{10 + 7 n}{6 + 5 n} \Rightarrow 18 + 15 n = 20 + 14 n$

or n=2

Hence, the answer is option (3).

Example 3: Consider a mixture of n moles of helium gas and 2n moles of oxygen gas (molecules taken to be rigid) as an ideal gas. Its C_p/C_v value will be :

1) 40/27

2) 23/15

3) 19/13

4) 67/45

Solution:

For monoatomic gas (He)

$c_{v} = \frac{3 R}{2}, c_{p} = \frac{5 R}{2}$

For diatomic gas $(O_{2})$
$\begin{aligned} c_{v} = \frac{5 R}{2}, c_{p} = \frac{7 R}{2} \\ γ_{mixure} = \frac{C_{p_{mix}}}{C_{v_{m x}}} = \frac{(n_{1} C_{p_{1}} + n_{2} C_{p_{2}})}{(n_{1} C_{v_{1}} + n_{2} C_{v_{2}})} \\ = \frac{n \frac{5}{2} R + 2 n \frac{7}{2} R}{n \frac{3}{2} R + 2 n \frac{5}{2} R} = \frac{19}{13} \end{aligned}$

Hence, the answer is the option (3).

Example 4: Two moles of an ideal gas with $\frac{C_{p}}{C_{v}} = \frac{5}{3}$ are mixed 3 moles of another ideal gas with $\frac{C_{p}}{C_{v}} = \frac{4}{3}$ . The value of $\frac{C_{p}}{C_{v}}$ for the mixture is:-

1) 1.50
2) 1.45
3) 1.47
4) 1.42

Solution:

For ideal gas:- $C_{p} - C_{v} = R$
For first case:-
$\begin{aligned} \frac{C_{p 1}}{C_{v 1}} = \frac{5}{3} and C_{p 1} - C_{v 1} = R \\ C_{p 1} = \frac{5}{3} C_{v 1} and \frac{5}{3} C_{v 1} - C_{v 1} = R \Rightarrow \frac{2}{3} C_{v 1} = R \Rightarrow C_{v 1} = \frac{3}{2} R \end{aligned}$

So, $C_{p 1} = \frac{5}{2} R$
For second case:-
$\begin{aligned} \frac{C_{p 2}}{C_{v 2}} = \frac{4}{3} and C_{p 2} - C_{v 2} = R \\ C_{p 2} = \frac{4}{3} C_{v 2} and \frac{4}{3} C_{v 2} - C_{v 2} = R \Rightarrow C_{v 2} = 3 R and C_{p 2} = 4 R \\ Y_{m i x} = \frac{n_{1} C_{p 1} + n_{2} C_{p 2}}{n_{1} C_{v 1} + n_{2} C_{v 2}} = \frac{2 \times \frac{5}{2} R + 3 \times 4 R}{2 \times \frac{3}{2} R + 3 \times 3 R} = 1.417 = 1.42 \end{aligned}$

Hence, the answer is the option (4).

Example 5: Two moles of helium gas are mixed with three moles of hydrogen molecules (taken to be rigid). What is the molar specific heat (in J/mol K) of the mixture at constant volume? (R=8.3 J/mol K)

1) 15.7

2) 17.4

3) 19.7

4) 21.6

Solution:

$\begin{aligned} C_{v mix} = \frac{n_{1} C_{v_{1}} + n_{2} C_{v_{2}}}{n_{1} + n_{2}} \\ = \frac{2 \times \frac{3}{2} R + 3 \times \frac{5}{2} R}{2 + 3} \\ = \frac{3 R + 15 \frac{R}{2}}{5} \\ = (\frac{21}{10}) R = \frac{21}{10} \times 8.314 \\ = 17.4 J / molK \end{aligned}$

Hence the answer is the option (2).

Summary

Mayer’s Law is a basic equation in thermodynamics relating the specific heat capacities of a gas at constant pressure denoted by Cp and at a constant volume Cv. His law states that the difference between the specific heat capacity at constant pressure Cp and the specific heat capacity at constant volume is equal to the gas constant R. With this principle, we can be able to know how gases take in heat and release it under varying circumstances.