Minimum Mass Hung from the String to Just Start the Motion

Suppose that you try to drag a heavy book along a desk by attaching a string and then pulling on the string with a small weight. You find that as long as the weight is less than a certain amount, the book does not budge, but if the weight exceeds this amount, the book just begins to slide along the table. This is a very important concept in physics, namely, the minimum force needed to overcome static friction and start something moving.

In this article, we are going to find out what minimum mass has to be hung from a string just to start the motion of an object. This misdemeanour concept helps us get familiar with the forces involved in statics. In this problem two types of forces participate, one is static friction and the other is tension. This article shows how to calculate the minimum mass, overcome static friction, to start to move. This concept falls under the broader category of law of motion which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. in the last decade of JEE Main, no direct question was asked but in NEET one questions were asked from this concept.

Minimum Mass Hung from the String to Just Start the Motion

We mainly experience two types of scenarios: one in which the mass is placed on a rough horizontal plane, and the other in which the mass is kept on an inclined plane.

When a Mass m₁ is Placed On a Rough Horizontal Plane

The tension in the string will try to move block m₁. As the Tension increases the friction will also increase till it reaches its maximum value (limiting friction). The given situation can result in two cases-

(a) Both blocks are at rest

From the FBD:

For block m₂-

$
\mathrm{T}=\mathrm{m}_2 \mathrm{~g} \ldots
$

For block $\mathrm{m}_1$.
$
\mathrm{R}=\mathrm{m}_1 \mathrm{~g}
$

Limiting friction-
$
\begin{aligned}
& \mathrm{fl}=\mu \mathrm{R}=\mu \mathrm{m}_1 \mathrm{~g} \\
& \mathrm{f}=\mathrm{T} \ldots(2)
\end{aligned}
$

From equation (1) and (2)

$
\begin{aligned}
& \mathrm{f}=\mathrm{m}_2 \mathrm{~g} \\
& \mathrm{f} \leq \mathrm{fl} \\
& \mathrm{m}_{2 \mathrm{~g}} \leq \mu \mathrm{m}_{1 \mathrm{~g}} \\
& \Rightarrow \mathrm{m}_2 \leq \mu \mathrm{m}_1
\end{aligned}
$

For Limiting cases-

$\Rightarrow \mathrm{m}_2=\mu \mathrm{m}_1$

(b) When both blocks are accelerated

$\mathrm{m}_1 \leq \mu \mathrm{m}_2$

When a Mass m₁ is Placed on a Rough Inclined Plane

When a mass ${m}_1$ placed on a rough inclined plane: Another mass $m_2$ hung from the ng connected by the pulley, the tension ( $T$ ) produced in the string will try to start the motion of $\mathrm{ssm} m_1$.

At limiting condition
For $m_2 \quad T=m_2 g .... (i)$ $\qquad$
For $m_1 \quad T=m_1 g \sin \theta+F.... (ii)$

$\Rightarrow T=m_1 g \sin \theta+\mu R$
$
\Rightarrow T=m_1 g \sin \theta+\mu m_1 g \cos \theta
$

From equation (i) and (ii)

$m_2=m_1[\sin \theta+\mu \cos \theta]$
this is the minimum value of $m_2$ to start the motion

And,

$\mu=\left[\frac{m_2}{m_1 \cos \theta}-\tan \theta\right]$

Recommended Topic Video

Solved Example Based On Minimum Mass Hung From the String to Just Start the Motion

Example 1: A block of mass $m_1=10 \mathrm{~kg}$ is placed on a horizontal rough surface $[\mu=0.5]$ is connected by another mass $m_2$ by a massless string as shown in the figure. What should be the minimum value of $m_2$ (in kg) to just start the motion?

1) 5

2) 7

3) 2

4) 10

Solution:

Minimum mass hung to start Motion -

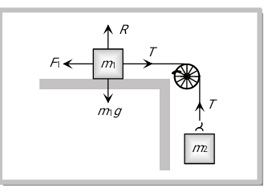
When m₁ is placed on a table (rough)

For liming condition
$
\begin{aligned}
& T=F_l \\
& m_2 g=\mu R \\
& m_2 g=\mu m_1 g \\
& m_2=\mu m_1 \\
& \quad \mu=\frac{m_2}{m_1}
\end{aligned}
$
- wherein
$\mathrm{T}=$ Tension in string
$F_l=$ Limiting friction
$\mu=$ Coefficient of friction

For Limiting Value
$
\begin{aligned}
& T=f_r=\mu N=\mu m_1 g \\
& T_2=m_2 g=\mu m_1 g \\
& m_2=\mu m_1=0.5 * 10=5 k g
\end{aligned}
$

Hence, the answer is option (1).

Example 2: Arrangement is shown in the given figure. If the coefficient of friction between the 2kg block and the table is 0.2. What would be the maximum mass (in kg) value of block B. So that the two blocks do not move. (10=m/s²)

1) 0.4

2) 0.2

3) 4

4) 2

Solution:

Minimum mass hung to start Motion -

When m₁ is placed on a table (rough)

For liming condition
$
\begin{aligned}
& T=F_l \\
& m_2 g=\mu R \\
& m_2 g=\mu m_1 g \\
& m_2=\mu m_1 \\
& \quad \mu=\frac{m_2}{m_1}
\end{aligned}
$- wherein

$\mathrm{T}=$ Tension in string
$F_l=$ Limiting friction
$\mu=$ Coefficient of friction

$
T=\mu m_A g
$

For block B
$
T=m_B g
$
for equilibrium
$
\begin{aligned}
& T=\mu m_A g=m_B g \\
& m_B=\mu m_A=0.2 * 2=0.4 \mathrm{~kg}
\end{aligned}
$

Hence, the answer is option (1).

Example 3: Two masses m₁= 5 kg and m₂=10 kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of the horizontal surface is 0.15. The minimum weight m (in kg) that should be put on top of m₂ to stop the motion is : (give answer till 2 decimal places)

1) 23.33

2) 18.3

3) 10.3

4) 43.3

Solution:

As we learnt in

Minimum Mass Hung from the String to Just Start the Motion -

Here m₁ is connected to one end of the string and m₂ is connected to another end of the string. And mass m₂ hung from the string connected by the pulley,

Case 1:-

When a mass m₁ is placed on a rough horizontal plane

So the tension (T) produced in the string will try to start the motion of mass m₁:

For liming condition

$
\begin{aligned}
& T=F_l \\
& m_2 g=\mu R \\
& m_2 g=\mu m_1 g
\end{aligned}
$
$m_2=\mu m_{1=\text { minimum value of }} \mathrm{m}_2$ to start the motion
$\mu=\frac{m_2}{m_1}$
where $\mathrm{T}=$ Tension in a string
$F_l=$ Limiting friction
$\mu=$ Coefficient of friction

In equilibrium
$
\begin{aligned}
& m_1 g=\mu\left(m+m_2\right) \\
& \quad m=\frac{m_1}{\mu}-m_2=\frac{5}{0.15}-10 \\
& m=23.33 \mathrm{~kg}
\end{aligned}
$

Hence, the answer is option (1).

Summary

The aim of this article was to describe the minimum mass that is to be hanged to a string Suspended to start its motion. Static frictional force seems to cause the object to start moving. Thus, it concludes the discussion of the minimum force calculation that is required to start motion by calculating the coefficient of static friction and the weight of an object. We also demonstrated that the string tension rises as mass is added on, up to the point at which it equals or exceeds the static friction force.

Additionally, we demonstrated that string tension increases with added mass until it equals or exceeds the static friction force. Understanding the interaction between static friction, tension, and weight allows us to solve the problem of initiating motion.