Moment Of Inertia Of A Rectangular Plate

The moment of inertia of a rigid body about a given axis of rotation is the sum of the products of the masses of the various particles and squares of their perpendicular distance from the axis of rotation. A crucial component of the larger field of rotational dynamics in physics is the moment of inertia of a rectangular plate with respect to its edge and centre.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Moment of Inertia of A Rectangular Plate
2. Solved Examples Based on A Rectangular Plate
3. Summary

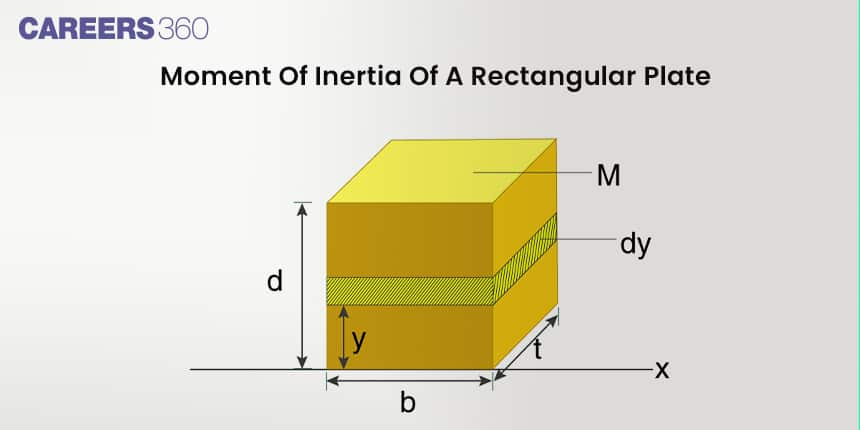
In this article, we will cover the concept of the moment of inertia of a rectangular plate. This topic falls under the broader category of rotational motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), more than four questions have been asked on this concept. It's also an important topic for NEET point of view.

Let's read this entire article to gain an in-depth understanding of the moment of inertia of a rectangular rod.

Moment of Inertia of A Rectangular Plate

$\text { Let } I_{y y}=$ Moment of inertia for uniform rectangular lamina about y-axis passing through its centre.

$\text { To calculate } I_{y y}$

Consider a uniform rectangular lamina of length l, and breadth b and mass M

Mass per unit area of rectangular lamina $=\sigma=\frac{M}{A}=\frac{M}{l \times b}$

Take a small element of mass dm with length dx at a distance x from the y-axis as shown in the figure.

$
\begin{aligned}
& d m=\sigma d A=\sigma(b d x) \\
& \Rightarrow d I=x^2 d m
\end{aligned}
$

Now integrate this dl between the limits $\frac{-l}{2}$ to $\frac{l}{2}$

$I_{y y}=\int d I=\int x^2 d m=\int_{\frac{-1}{2}}^{\frac{1}{2}} \frac{M}{l b} x^2 *(b) d x=\frac{M}{l} \int_{\frac{-1}{2}}^{\frac{1}{2}} x^2 d x=\frac{M l^2}{12}$

Similarly,

Let = Moment of inertia for uniform rectangular lamina about the x-axis passing through its centre.

To calculate

Take a small element of mass dm with length dx at a distance x from the x-axis as shown in the figure.

mass per unit Area of rectangular lamina =

Now integrate this dI between the limits

$I_{x x}=\int d I=\int x^2 d m=\int_{\frac{-b}{2}}^{\frac{b}{2}} \frac{M}{l b} x^2 *(l) d x=\frac{M}{b} \int_{\frac{-b}{2}}^{\frac{b}{2}} x^2 d x=\frac{M b^2}{12}$

Recommended Topic Video

Solved Examples Based on A Rectangular Plate

Example 1: If $I=$ Moment of inertia for uniform rectangular lamina of length $l$, and breadth $b$ and mass $M$ about an axis passing through its centre and perpendicular to its breadth. Then I will be equal to:

1) $\frac{M b^2}{12}$
2) $\frac{M l^2}{12}$
3) $\frac{M l^2}{6}$
4) $\frac{M b^2}{6}$

Solution:

From the figure, we can say that

$I_{x x}=I=\frac{M b^2}{12}$

Hence, the correct option is (1).

Example 2: The moment of inertia for a rectangular lamina about the axis in the plane of lamina passing through the end and parallel to the breadth is:

1) $\frac{m l^2}{12}$
2) $\frac{m l^2}{4}$
3) $\frac{m l^2}{3}$
4) $\frac{m l^2}{2}$

Solution

The axis is in the plane of the lamina passing through the end & parallel to the breadth.

The mass distribution of lamina in the above case is like a rod for which the axis passes through its end hence the moment of inertia for a rectangular lamina about the axis in the plane of lamina passing through the end and parallel to the $\text { breadth is } \frac{M l^2}{3} \text { }$

Hence, the answer is the option (3).

Example 3: From a solid sphere of mass M and radius R a cube of maximum possible volume is cut. The moment of inertia of a cube about an axis passing through its centre and perpendicular to one of its faces is :

1) $\frac{M R^2}{32 \sqrt{2} \pi}$
2) $\frac{M R^2}{16 \sqrt{2} \pi}$
3) $\frac{4 M R^2}{9 \sqrt{3} \pi}$
4) $\frac{4 M R^2}{3 \sqrt{3} \pi}$

Solution:

$\begin{aligned}
& a=\frac{2}{\sqrt{ } 3} R \\
& \frac{M}{M^{\prime}}=\frac{\frac{4}{3} \pi R^3}{a^3}=\frac{\frac{4}{3} \pi R^3}{\left(\frac{2}{\sqrt{3}^3} R\right)^3} \Rightarrow \frac{M}{M^{\prime}}=\frac{\frac{4}{3} \pi R^3}{\frac{8}{3 \sqrt{3}} R^3}=\frac{4 \pi}{3} \times \frac{3 \sqrt{3}}{8} \\
& \frac{M}{M^{\prime}}=\frac{\sqrt{3} \pi}{2} \Rightarrow M^{\prime}=\frac{2 M}{\sqrt{3} \pi}
\end{aligned}$

M.O.I. of the cube about the given axis.

$I=\frac{M^{\prime} a^2}{6}=\frac{\frac{2 M}{\sqrt{3} \pi} \times\left(\frac{2}{\sqrt{3}} R\right)^2}{6}=\frac{4 M R^2}{9 \sqrt{3} \pi}$

Hence, the answer is the option (3).

Example 4: For a uniform rectangular sheet shown in the figure, the ratio of moments of inertia about the axes perpendicular to the sheet and passing through O (the centre of mass) and O' (corner point ) is:

1) $\frac{2}{3}$
2) $\frac{1}{4}$
3) $\frac{1}{8}$
4) $\frac{1}{2}$

Solution:

$\begin{aligned}
& \mathrm{I}_{\mathrm{O}}=\frac{\mathrm{M}}{12}\left[\mathrm{~L}^2+\mathrm{B}^2\right]=\frac{\mathrm{M}}{12}\left[80^2+60^2\right] \\
& \mathrm{I}_{\mathrm{O}^{\prime}}=\mathrm{I}_0+\mathrm{Md}^2\{\text { parallel axis theorem } \\
& =\frac{\mathrm{M}}{12}\left[80^2+60^2\right]+\mathrm{M}[50]^2 \\
& \frac{\mathrm{I}_{\mathrm{O}}}{\mathrm{I}_{\mathrm{O}^{\prime}}}=\frac{\mathrm{M} / 12\left[80^2+60^2\right]}{\frac{\mathrm{M}}{2}\left[80^2+60^2\right]+\mathrm{M}\left[50^2\right.}=\frac{1}{4}
\end{aligned}$

Hence, the answer is the option (4).

Example 5: The moment of inertia of a square plate of side about the axis passing through one of the corners and perpendicular to the plane of the square plate is given by:

1) $\frac{\mathrm{M} l^2}{6}$
2) $\frac{2}{3} \mathrm{M} l^2$
3) $\mathrm{Ml}^2$
4) $\frac{M l^2}{12}$

Solution:

$\begin{aligned}
& I_{c o M}=\frac{M}{12}\left(L^2+L^2\right)=\frac{M L^2}{6} \\
& I_0=I_{C O M}+M d^2 \\
& \quad=\frac{M L^2}{6}+M\left(\frac{L}{\sqrt{2}}\right)^2=\frac{M L^2}{6}+\frac{M L^2}{2} \\
& I_0=\frac{4 M L^2}{6}=\frac{2}{3} M L^2
\end{aligned}$

Summary

The moment of inertia is applied in both linear and angular moments, although it manifests itself in planar and spatial movement in rather different ways. We got you the derivations of how to calculate the moment of inertia of a rectangular plate, along with the derivation of the moment of inertia of a rectangular plate about its centre, and the moment of inertia of a rectangular plate about its edge as well.