Moment Of Inertia Of A Rod

The moment of inertia of a rigid body about a given axis of rotation is the sum of the products of the masses of the various particles and squares of their perpendicular distance from the axis of rotation. When a thin rod's linear mass density, or mass per length, remains constant throughout its length, it is said to be uniform.

This Story also Contains

1. Definition of Moment of Inertia
2. Radius of Gyration (K)
3. Moment of Inertia of a Rod
4. Summary

In this article, we will cover the concept of the moment of inertia of a rod. This topic falls under the broader category of rotational motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), five questions have been asked on this concept. And for NEET one question was asked from this concept.

Let's read this entire article to gain an in-depth understanding of the moment of inertia of a rod.

Definition of Moment of Inertia

The moment of inertia (I) of a body is a measure of its ability to resist change in its rotational state of motion. It plays the same role in rotatory motion as is played by mass in translatory motion.

Formula of Moment of Inertia
Moment of inertia of a particle I=mr2

Where: m is the mass of particle and r is the perpendicular distance of the particle from the rotational axis.

Moment of Inertia For System of Particle
I=m1r12+m2r22+………mnrn2=∑i=1nmiri2

(This is Applied when masses are placed discreetly)

Moment of Inertia For Continuous Body
I=∫r2dm

Where: r is the perpendicular distance of a particle of mass dm of a rigid body from the axis of rotation

- Dimension =[ML2]
- S.I. unit =kg−m2

It depends on mass, distribution of mass and on the position of the axis of rotation.
It does not depend on angular velocity, angular acceleration, torque, angular momentum and rotational kinetic energy.
It is a tensor quantity.

Radius of Gyration (K)

Radius of Gyration of a body about an axis is the effective distance from the axis where the whole mass can be assumed to be concentrated so that the moment of inertia remains the same.

Formula- K=IM
or, I=MK2

• It does not depend on the mass of the body
• It depends on the shape and size of the body, distribution of mass of the body w.r.t. the axis of rotation etc.
• Dimension-
• S.I. unit: Meter.

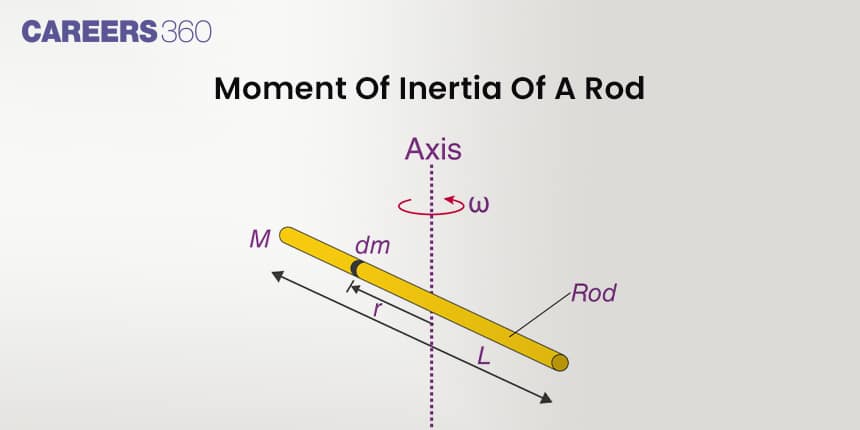
Moment of Inertia of a Rod

Let I=Moment of inertia of a ROD about an axis through its centre and perpendicular to it, to calculate I (Moment of inertia of rod).

Consider a uniform straight rod of length L, mass M and having centre C.

mass per unit length of the rod:
λ=ML

Take a small element of mass dm with length dx at a distance x from point C.

dm=λ⋅dx=ML⋅dx⇒dI=x2dm

Now integrate this dl between the limits x=−L2 to L2

I=∫dI=∫x2dm=∫−L2L2MLx2∗dx=ML∫−L2L2x2dx=ML212

Recommended Topic Video

Solved Examples Based on Moment of Inertia of a Rod

Example 1: The moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is I. What is the ratio lR such that the moment of inertia is minimum?

1) 32
2) 32
3) 1
4) 32

Solution:

The length of the Cylinder =l
Radius of cylinder =R
Moment of inertia =l
Moment of inertia of uniform rod of length(I) -
I=Ml212

wherein

About axis passing through its centre & perpendicular to its length.

We know that a solid cylinder is about an axis that is perpendicular bisector.

I=mR24+ml212=m4[R2+l23]I=m4[πlR2πl+l23]=m4[vπl+l23] putting πlR2=vdIdl=0⇒m4[−vπl2+2l3]=0⇒−vπl2+2l3=0vπl2=2l3⇒v=2πl33πR2l=2πl33⇒R2=2l23l2R2=32lR=32

Hence, the answer is the option (1).

Example 2: A thin uniform bar of length L and mass 8 m lies on a smooth horizontal table. Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively. The masses stick to the bar after collision at a distance L/3 and L/6 respectively from the centre of the bar. If the bar starts rotating about its centre of mass as a result of the collision, the angular speed of the bar will be :

1) v5L
2) 6v5L
3) 3v5L
4) v6L

Solution:

Moment of inertia of uniform rod of length (l) -
I=Ml212

About axis passing through its centre \& perpendicular to its length.
Law of conservation of angular moment -
τ→=dL→dt

If net torque is zero
i.e. dL→dt=0
L→= constant

angular momentum is conserved only when external torque is zero.

The centre of mass of the system from o
=8m×0+m(L/3)−2m(L/6)8m+m+2m=0

So, the centre of mass is at "O".
From the conservation of angular momentum;
Li=LfLi=m⋅(2v)∗(L/3)+2mv∗(L/6)=mvLLf=[(8m)⋅L212+m⋅(L/3)2+2m⋅(L/6)2]ω

=[23mL2+mL29+mL218]ω=(12+2+118)mL2ω=56mL2ω56mL2ω=mvL∴ω=6v5L

Example 3: A uniform thin rod of length 4l, mass 4m is bent at the points as shown in the figure. What is the moment of inertia of the rod about the axis passing through point O & perpendicular to the plane of the paper?

1) ml23
2) 10ml23
3) ml212
4) ml224

Solution:

Moment of inertia of uniform rod of length (l)
I=Ml212

About axis passing through its centre \& perpendicular to its length.
The given structure can be broken into 4 parts
For AB:I=ICM+m×d2=ml212+5m4l2;IAB=43ml2

For BO: I=ml23
For composite frame : (by symmetry)
I=2[IAB+IOB]=2[4ml23+ml23]=103ml2.

Example 4: Three identical rods, each of length l are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is:

1) l
2) l/2
3) l/2
4) l/3

Solution:

Radius of gyration (K)

The radius of Gyration of a body about an axis is the effective distance from the axis where the whole mass can be assumed to be concentrated so that the moment of inertia remains the same.

wherein

I=MK2K=IM

MI of system w.r.t an axis perpendicular to the plane and passing through one centre

=ml23+ml23+[ml212+m[3l2]2]=2ml23+10ml212=1812ml2NOW3mk2=32ml2k=l/2

Example 5: A uniform straight rod of length L, mass M has Moment of inertia about an axis through its centre and perpendicular to it as I. If we take the new rod of length 2L, and mass (0.5M), Then the Moment of inertia of the new rod about an axis through its centre and perpendicular to it will be:

1) I

2) 2I

3) 3I

4) 4I

Solution:

The moment of inertia of a Rod is given as I=ML212 Now take M′=0.5M and L′=2L
so, I′=M′L′212=12M×4L212=2I

Hence, the answer is the option 2.

Summary

The moment of inertia for a rigid body is a physical quantity that combines mass and shape in Newton's equations of motion, momentum, and kinetic energy. The moment of inertia is applied in both linear and angular moments, although it manifests itself in planar and spatial movement in rather different ways. One scalar quantity defines the moment of inertia in planar motion.