Moment Of Inertia Of The Solid Cylinder

The inability of a body to change its state of rest or of uniform linear motion by itself is known as inertia. A body rotating about an axis is unable to produce a change in its rotational motion by itself and this inertness in the case of rotational motion is known as rotational inertia.

In this article, we will cover the concept of the moment of inertia of a solid cylinder. This topic falls under the broader category of rotational motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), almost three questions have been asked on this concept. But no direct question was asked in the NEET Exam.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Moment of Inertia of the Solid Cylinder
2. Solved Example Based on the Moment of Inertia of the Solid Cylinder
3. Summary

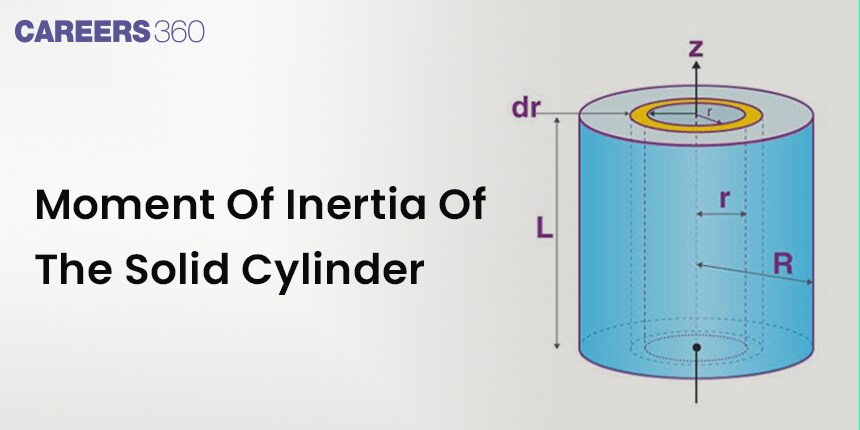
Moment of Inertia of the Solid Cylinder

Let I= Moment of inertia of the cylinder about an axis through its centre

To calculate I

Consider a cylinder of mass M, radius R and length L.

mass per unit volume of the cylinder $\rho=\frac{M}{V}=\frac{M}{\pi R^2 L}$

Imagine that the cylinder is made of a large number of coaxial cylindrical shells

Take a small elemental cylindrical shell of mass dm having internal radius x and external radius (x + dx).

So for that elemental cylindrical shell $d V=(2 \pi x d x) L$

And
$
dm=\rho d V=\frac{M}{\pi R^2 L}(2 \pi x d x) L
$

Now integrate this dI between the limits x=0 to x=R

$\begin{aligned}
& I=\int d I=\int x^2 * \rho d v \\
& =\int_0^R \frac{M}{\pi R^2 L}\left(2 \pi * L x^3 d x\right) \\
& =\frac{2 M}{R^2} \int_0^R x^3 d x=\frac{M R^2}{2}
\end{aligned}$

Recommended Topic Video

Solved Example Based on the Moment of Inertia of the Solid Cylinder

Example 1: The moment of inertia of solid cylinder mass M, length L and radius R about its own axis is:

1) $M R^2$
2) $M L^2$
3) $\frac{M R^2}{2}$
4) $\frac{M L^2}{12}$

Solution:

Moment of inertia for solid cylinder -

$
I=\frac{1}{2} M R^2
$
wherein
About the axis passing through a central line.
The moment of inertia about its own axis is $\frac{M R^2}{2}$

Hence, the answer is option (3).

Example 2: Two solid cylinders are connected by a massless rod as shown in the figure. The distance b/w centre line of both cylinders is 3R. What is the moment (in terms of MR²) of inertia of the system about the axis shown in the below diagram?

1) 5.55

2) 6.25

3) 1.85

4) 1.6

Solution:

Moment of inertia for solid cylinder About axis passing through central line is given by:
$
I_c=\frac{1}{2} M R^2
$

For the figure

For cylinder 1

$\begin{gathered}
I_1=I_c+M d^2 \\
I_1=\frac{1}{2} M R^2+M\left[R+\frac{R}{3}\right]^2 \\
\frac{1}{2} M R^2+M\left[\frac{4 R}{3}\right]^2=\frac{41}{18} M R^2
\end{gathered}$

For cylinder 2

$\begin{aligned}
& I_2=I_c+M d^2 \\
I_2= & \frac{1}{2} M R^2+M\left[R+\frac{2 R}{3}\right]^2 \\
I_2= & \frac{59}{18} M R^2
\end{aligned}$

So,

$I=I_1+I_2=\frac{41}{18} M R^2+\frac{59}{18} M R^2=\frac{100}{18} M R^2=\frac{50}{9} M R^2$

Hence, the answer is option (1).

Example 3: The moment of inertia of a cylinder of mass $M$ and length $L$ and radius $\mathrm{R}$ about an axis passing through its centre and perpendicular to the axis of the cylinder is $I=M\left(\frac{R^2}{4}+\frac{L^2}{12}\right)$ If such a cylinder is to $\frac{L}{R}$ for it to have the be made for a given mass of a material, the ratio $\bar{R}$ for it to have the minimum possible I is:

1) $\frac{2}{3}$
2) $\frac{3}{2}$
3) $\sqrt{\frac{2}{3}}$
4) $\sqrt{\frac{3}{2}}$

Solution:

$
I=m\left[\frac{R^2}{4}+\frac{L^2}{12}\right]
$

Given,
$
M=\rho\left(\pi R^2 L\right)
$

So,
$
I=M\left[\frac{R^2}{4}+\frac{M^2}{\left.12\left(\rho \pi R^2\right)^2\right)}\right]
$

$
\begin{aligned}
& \frac{d I}{d R}=0 \\
\Rightarrow & M\left[\frac{2 R}{4}+\frac{-4 M^2}{12 \rho^2 \pi^2 R^5}\right]=0 \\
R= & (2 / 3)^{1 / 6} \times\left(\frac{M}{\rho \pi}\right)^{1 / 3} \ldots( 1)\\
L= & \frac{M}{\rho \pi\left(\frac{2}{3}\right)^{1 / 3}\left(\frac{M}{\rho \pi}\right)^{2 / 3}} \ldots(2)
\end{aligned}
$

So, (2) divided by (1) will give
$
\frac{L}{R}=\sqrt{\frac{3}{2}}
$

Hence, the answer is the option (4).

Example 4: The solid cylinder of length 80 cm and mass M has a radius of 20 cm. Calculate the density of the material used if the moment of inertia of the cylinder about an axis CD parallel to AB as shown in the figure is 2.7 kg m².

1) $1.49 \times 10^2 \frac{\mathrm{kg}}{\mathrm{m}^3}$
2) $7.5 \times 10^1 \frac{\mathrm{kg}}{\mathrm{m}^3}$
3) $14 \cdot 9 \frac{\mathrm{kg}}{\mathrm{m}^3}$
4) $7.5 \times 10^2 \frac{\mathrm{kg}}{\mathrm{m}^3}$

Solution:

$\begin{aligned}
& I_{C D}=I_{A B}+M d^2 \\
& \quad=\left(\frac{M R^2}{2}\right)+M\left(\frac{L}{2}\right)^2 \\
& 2 \cdot 7=\left(\frac{M \times 0 \cdot 04}{2}\right)+\left(\frac{M \times 0 \cdot 64}{4}\right) \\
& 10 \cdot 8=0 \cdot 08 \mathrm{M}+0 \cdot 64 \mathrm{M} \\
& 10 \cdot 8=0 \cdot 72 \mathrm{M} \\
& M=\frac{10 \cdot 8}{0 \cdot 72}=15 \mathrm{~kg} \\
& M=\rho \times\left(\pi r^2 \mathrm{~L}\right) \\
& s=\frac{15}{\frac{22}{7} \times 0 \cdot 04 \times 0 \cdot 8} \\
& s=\frac{105}{22 \times 0 \cdot 04 \times 0 \cdot 8}=\frac{105 \times 10^{+3}}{22 \times 32} \\
& =0 \cdot 149 \times 10^3 \\
& s=1 \cdot 49 \times 10^2 \frac{\mathrm{kg}}{\mathrm{m}^3}
\end{aligned}$
Hence, the answer is option (1)

Example 5: A uniform solid cylinder with radius $\mathrm{R}$ and length $\mathrm{L}$ has a moment of inertia $\mathrm{I}_1$, about the axis of the cylinder. A concentric solid cylinder of radius $\mathrm{R}^{\prime}=\frac{\mathrm{R}}{2}$ and length $\mathrm{L}^{\prime}=\frac{\mathrm{L}}{2}$ is carved out of the original cylinder. If $\mathrm{I}_2$ is the moment of inertia of the carved-out portion of the cylinder then $\frac{\mathrm{I}_1}{\mathrm{I}_2}=$ $\qquad$ (Both $\mathrm{I}_1$ and $\mathrm{I}_2$ are about the axis of the cylinder)

1) 32

2) 34

3) 36

4) 38

Solution:

$\begin{aligned}
& \mathrm{I}_1=\frac{\mathrm{MR}^2}{2} \\
& \text { mass }=\rho \pi \frac{\mathrm{R}^2}{4} \cdot \frac{\mathrm{L}}{2} \\
& \mathrm{~m}_2=\frac{\mathrm{M}}{8} \\
& \mathrm{I}_2=\frac{\mathrm{m}_2 \mathrm{R}_2^2}{2}=\frac{\mathrm{MR}^2}{8 \times 4 \times 2} \\
& \frac{\mathrm{I}_1}{\mathrm{I}_2}=32
\end{aligned}$

Hence, the answer is option (1).

Summary

A moment of inertia is a revolving object; for this reason, a moment of inertia is also known as angular momentum or acceleration. But as the name implies, moment of inertia is for angular or rotational motion, whereas inertia is for linear motion. This makes it very distinct from linear inertia. The size and shape of the object's cross-section, such as its I, circular, or rectangular cross-section, among others, are some of the factors that determine the moment of inertia. Another factor is the object's density, and the distribution of particles and objects about the rotational axis is the last and most important factor.