Moment of inertia

The moment of inertia of a rigid body about a given axis of rotation is the sum of the products of the masses of the various particles and squares of their perpendicular distance from the axis of rotation.

In this article, we will cover the concept of moment of inertia. This topic falls under the broader category of rotational motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Generally, this concept is used to solve various questions in exams.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Definition of Moment of Inertia
2. Radius of Gyration (K)
3. Solved Examples Based On Moment Of Inertia
4. Summary

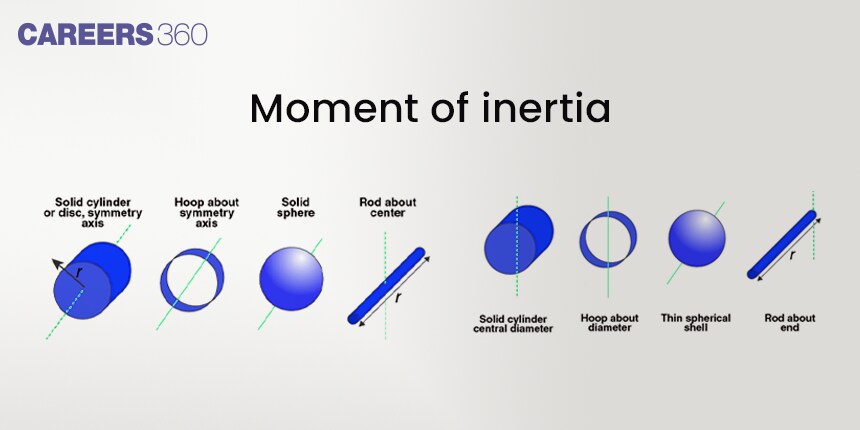
Let's read this entire article to gain an in-depth understanding of the moment of inertia.

Definition of Moment of Inertia

Moment of inertia (I) of a body is a measure of its ability to resist change in its rotational state of motion. It play the same role in rotatory motion as is played by mass in translatory motion.

Formula

$\text { Moment of inertia of a particle } I=m r^2$

Where: m is the mass of the particle and r is the perpendicular distance of the particle from the rotational axis.

Moment of Inertia For System of Particle

$\begin{aligned}
& I=m_1 r_1^2+m_2 r_2^2+\ldots \ldots \ldots m_n r_n^2 \\
= & \sum_{i=1}^n m_i r_i^2
\end{aligned}$

(This is Applied when masses are placed discreetly)

Moment of Inertia For Continuous Body

$I=\int r^2 d m$

Where: r is the perpendicular distance of a particle of mass dm of a rigid body from the axis of rotation

- Dimension $=\left[M L^2\right]$
- S.I. unit $=k g-m^2$

• It depends on mass, distribution of mass and on the position of the axis of rotation.
• It does not depend on angular velocity, angular acceleration, torque, angular momentum and rotational kinetic energy.
• It is a tensor quantity.

Radius of Gyration (K)

Radius of Gyration of a body about an axis is the effective distance from the axis where the whole mass can be assumed to be concentrated so that the moment of inertia remains the same.

• Formula- $K=\sqrt{\frac{I}{M}}$
  or, $I=M K^2$

• It does not depend on the mass of the body

• It depends on the shape and size of the body, distribution of mass of the body w.r.t. the axis of rotation etc.

• Dimension- $M^o L^1 T^o$

• S.I. unit: Meter.

Recommended Topic Video

Moment of Inertia of Two Point Masses About Their Centre of Mass

Let two masses m₁ and m₂ at a distance r and from their centre of mass they are at a distance r₁ and r₂ respectively.

Then,

$
\begin{aligned}
& r_1+r_2=r_1 \\
& m_1 r_1=m_2 r_2
\end{aligned}
$

From equation (1) and (2)
$
r_1=\frac{m_2}{m_1+m_2} * r
$

And,
$
r_2=\frac{m_1}{m_1+m_2} * r
$
$
\begin{aligned}
& I=I_1+I_2=m_1 r_1^2+m_2 r_2^2 \\
& I=\frac{m_1 m_2}{m_1+m_2} * r^2 \\
& I_1=m_2 I, \text { and } I_2=m_1 I
\end{aligned}
$

Recommended Topic Video

Solved Examples Based On Moment Of Inertia

Example 1: Four point masses (each of mass m) are arranged in the x-y plane. The moment inertia of masses about the y-axis is :

1) $6 m a^2$
2) $4 m a^2$
3) $2 m a^2$
4) $m a^2$

Solution:

Moment of inertia for the system of particle

$\begin{aligned}
& I=m_1 r_1^2+m_2 r_2^2+\ldots \ldots \ldots m_n r_n^2 \\
& =\sum_{i=1}^n m_i r_i^2
\end{aligned}$

So, Moment of inertia of masses= $m(0)^2+m(2 a)^2+m(a)^2+m(a)^2=6 m a^2$

Example 2: A massless equilateral triangle $E F G$ of side ' $a$ ' (As shown in the figure) has three particles of mass $m$ situated at its vertices. The moment of inertia of the system about the line $E X$ perpendicular to $E G$ in the plane of $E F G$ is $\frac{N}{20} m a^2$ where $N$ is an integer. The value of $N$ is:

1) 5

2) 10

3) 20

4) 25

Solution:

The moment of inertia of the system about the line passing through EX is
$
I=I_E+I_F+I_G
$

As we know for point mass $m$ at separation $\mathrm{r}$ from the axis of rotation is
$
I=m r^2
$

Point masses separation from the axis of rotation at positions $\mathrm{E}, \mathrm{F} \& \mathrm{G}$ are 0 , $a / 2$, a respectively
$
I=m(0)^2+m(a / 2)^2+m(a)^2=\frac{5 m a^2}{4}=\frac{25 m a^2}{20}
$
comparing with, $\frac{N}{20} m a^2$

N=25

Hence, the answer is option (4).

Example 3: A wheel of mass 10kg has a moment of inertia of 90 kg-m² about its own axis, the radius of the gyration will be:

1) 1

2) 2

3) 3

4) 4

Solution

$\begin{aligned}
& I=m K^2 \\
& 90=10\left(K^2\right) \\
& K=3
\end{aligned}$

Hence, the answer is the option (3).

Example 4: Let the moment of inertia of a hollow cylinder of length 30 cm (inner radius 10 cm and outer radius 20 cm ), about its axis be I. The radius (in cm) of a thin cylinder of the same mass such that its moment of inertia about its axis is also I, is :

1) 16

2) 18

3) 14

4) 12

Solution

Radius of gyration (K)

The radius of Gyration of a body about an axis is the effective distance from the axis where the whole mass can be assumed to be concentrated so that the moment of inertia remains the same.

wherein

$\begin{aligned}
& I=M K^2 \\
& K=\sqrt{\frac{I}{M}}
\end{aligned}$

$
I=\frac{m\left(20^2+10^2\right)}{2}
$
now let the moment of inertia of a thin cylinder
$
\begin{aligned}
& I=m k^2 \\
& I=m k^2=m \frac{20^2+10^2}{2} \\
& k=\sqrt{\frac{400+100}{2}}=5 \sqrt{10} \mathrm{~cm} \\
& k \approx 16 \mathrm{~cm}
\end{aligned}
$

Hence, the answer is option (1).

Summary

The moment of inertia for a rigid body is a physical quantity that combines mass and shape in Newton's equations of motion, momentum, and kinetic energy.
The moment of inertia is applied in both linear and angular moments, although it manifests itself in planar and spatial movement in rather different ways. One scalar quantity defines the moment of inertia in planar motion.