Motion Of A Charged Particle In Uniform Magnnetic Field

When a charged particle moves through a uniform magnetic field, its trajectory is significantly influenced by the Lorentz force, which acts perpendicular to both the magnetic field and the particle's velocity. This interaction causes the particle to follow a curved path, often resulting in circular or helical motion depending on its initial conditions. In everyday life, this principle is at work in devices like cyclotrons used in medical treatments and particle accelerators for research. The motion of charged particles in the Earth's magnetic field is also responsible for natural phenomena like the auroras, where charged particles from the solar wind are directed towards the poles, creating stunning displays of light. In this article, we will discuss the concept of motion of a charged particle in a uniform magnetic field and solve examples for concept clarity.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

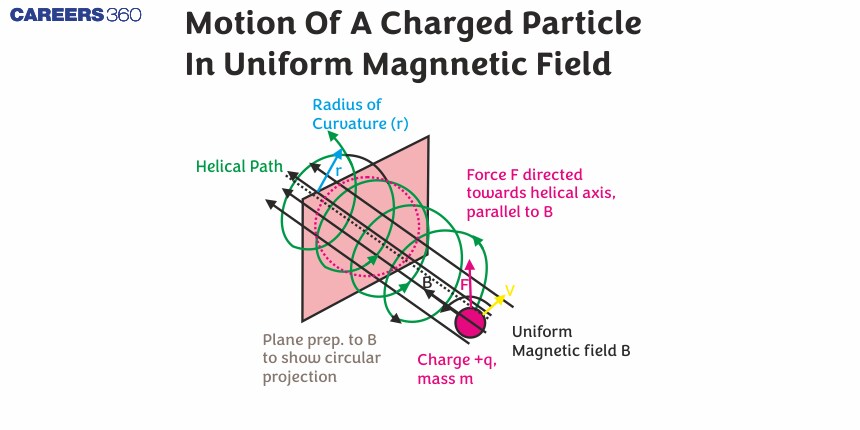
The Motion of a Charged Particle in a Uniform Magnetic Field

In the figure a negatively charged particle moves in the plane of the paper in a region where the magnetic field is perpendicular to the paper. The magnetic force is perpendicular to the velocity, so velocity changes in direction but not magnitude. The result is uniform circular motion. Note that because the charge is negative, the force is opposite in direction to the prediction of the right-hand rule.

In this situation, the magnetic force supplies the centripetal force $F_c=\frac{m v^2}{r}$. Noting that the velocity is perpendicular to the magnetic field, the magnitude of the magnetic force is reduced to $F=q v B$.. Because the magnetic force F supplies the centripetal force $F_c$ we have,

$q v B=\frac{m v^2}{r}$

Solving for r gives

$r=\frac{m v}{q B}$

Here, r is the radius of curvature of the path of a charged particle with mass m and charge q, moving at a speed v that is perpendicular to a magnetic field of strength B. The time for the charged particle to go around the circular path is defined as the period, which is the same as the distance travelled (the circumference) divided by the speed. Based on this and the Equation, we can derive the period of motion as:

$T=\frac{2 \pi r}{v}=\frac{2 \pi}{v} \frac{m v}{q B}=\frac{2 \pi m}{q B}$

Therefore frequency of revolution is

$\frac{1}{T}=\frac{q B}{2 \pi m}$

This frequency is called the cyclotron frequency.

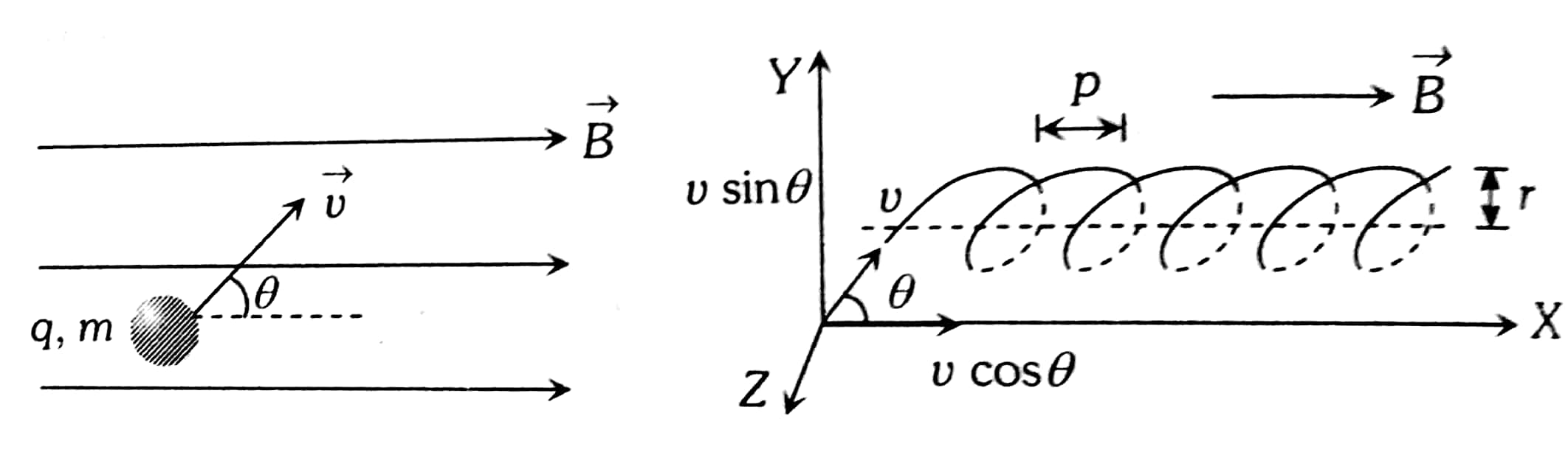
If the velocity is not perpendicular to the magnetic field, then we can compare each component of the velocity separately with the magnetic field. The component of the velocity perpendicular to the magnetic field produces a magnetic force perpendicular to both this velocity and the field.

The component parallel to the magnetic field creates constant motion along the same direction as the magnetic field, also shown in Equation. The parallel motion determines the pitch p of the helix, which is the distance between adjacent turns. This distance equals the parallel component of the velocity times the period:

$p=v_{\text {para }} T$

This results in a helical motion, as shown in the following figure:

While the charged particle travels in a helical path, it may enter a region where the magnetic field is not uniform. In particular, suppose a particle travels from a region of strong magnetic field to a region of a weaker field, and then back to a region of a stronger field. The particle may reflect back before entering the stronger magnetic field region. This is similar to a wave on a string travelling from a very light, thin string to a hard wall and reflecting backwards. If the reflection happens at both ends, the particle is trapped in a so-called magnetic bottle.

The radius of the helical path

$r=\frac{m(v \sin \theta)}{q B}$

Time period of the helical path

$T=\frac{2 \pi m}{q B}$

Frequency of helical path

$F=\frac{1}{T}=\frac{q B}{2 \pi m}$

Pitch: The pitch is the horizontal distance between two consecutive circles.

$P=(V \cos \theta) T=\frac{2 \pi m}{q B}(V \cos \theta)$

Solved Examples Based on Motion of a Charged Particle In Uniform Magnetic Field

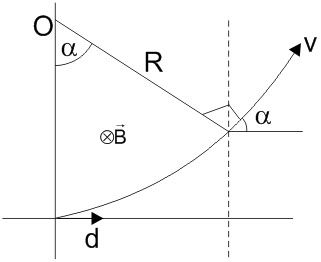
Example 1: A proton (mass m) accelerated by a potential difference V flies through a uniform transverse magnetic field B. The field occupies a region of space by width d. If the angle of deviation of the proton from the initial direction of motion (see figure), the value will be :

1) $\frac{B}{2} \sqrt{\frac{q d}{m V}}$
2) $\frac{B}{d} \sqrt{\frac{q}{2 m V}}$
3) $B d \sqrt{\frac{q}{2 m V}}$
4) $q V \sqrt{\frac{B d}{2 m}}$

Solution:

The radius of the charged particle

$r=\frac{m v}{q B}=\frac{P}{q B}=\frac{\sqrt{ } 2 m k}{q B}=\frac{1}{B} \sqrt{ } \frac{2 m V}{q}$

Energy of Proton $=\frac{1}{2} m v^2=q V$
$v=\sqrt{\frac{2 q V}{m}}$

Magnetic force
$q v B \sin 90^{\circ}=\frac{m v^2}{R}$
$
R=\frac{m v}{q B}
$

From the figure
$
\begin{aligned}
& \sin \alpha=\frac{d}{R}=\frac{q d B}{m v}=\frac{q d B}{m} \sqrt{\frac{m}{2 q V}} \\
& \therefore \sin \alpha=B d \sqrt{\frac{q}{2 m V}}
\end{aligned}
$

Hence, the answer is the option (3).

Example 2: An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii r_e, r_p, r_a respectively in a uniform magnetic field B. The relation between r_e, r_p, r_a is :

1)r_e < r_a < r_p

2) r_e > r_p = r_a

3) r_e < r_p = r_a

4)r_e < r_p < r_a

Solution:

The radius of the charged particle

$\begin{aligned} & r=\frac{m v}{q B}=\frac{P}{q B}=\frac{\sqrt{ } 2 m k}{q B}=\frac{1}{B} \sqrt{ } \frac{2 m V}{q} \\ & r=\frac{m v}{q B}=\frac{\sqrt{2 m E}}{q B} \\ & \frac{\sqrt{m_{\prec}}}{q_{\prec}}=\frac{\sqrt{m_p}}{q_p}>\frac{\sqrt{m_e}}{q_e} \\ & \therefore r_{\prec}=r_p>r_e\end{aligned}$

Hence, the answer is the option (3).

Example 3: The region between y = 0 and y = d contains a magnetic field $\vec{B}=B \hat{z}$ . A particle of mass m and charge q enters the region with a velocity $\vec{v}=v \hat{i}. if \quad d=\frac{m v}{2 q B}$,. , the acceleration of the charged particle at the point of its emergence at the other side is:

$
\begin{aligned}
& \text { 1) } \frac{q v B}{m}\left(-\frac{\sqrt{3}}{2} \widehat{i}+\frac{1}{2} \widehat{j}\right) \\
& \text { 2) } \frac{q v B}{m}\left(\frac{-\widehat{j}+\widehat{i}}{\sqrt{2}}\right) \\
& \text { 3) } \frac{q v B}{m}\left(\frac{\widehat{i}+\widehat{j}}{\sqrt{2}}\right)
\end{aligned}
$
4)None of these

Solution:

$\begin{aligned} & \sin \theta=\frac{d}{2 d} \Rightarrow \sin \theta=\frac{1}{2} \Rightarrow \theta=\frac{\pi}{6} \\ & \vec{a}=\frac{|q| \omega b}{m}(\cos \theta(-\hat{i})+\sin \theta \hat{j}) \\ & \vec{a}=\frac{|q| \omega b}{m}\left(-\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}\right)\end{aligned}$

Hence, the answer is the option (3).

Example 4: A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be

1)A straight line

2)A circle

3) A helix with a uniform pitch

4)A helix with a non-uniform pitch

Solution:

Helical path

When the charged particle is moving at an angle to the field particle describe a path called helix.

wherein

When a particle enters at angles other than $0^{\circ}$ or $90^{\circ}$ or $180^{\circ}$ path followed is a helix.

Hence, the answer is the option (3).

Example 5: A charged particle of mass m and charge q describes the helical motion of radius r in a uniform magnetic field of strength B. The time of revolution is

1) $\frac{B q}{2 \pi m}$
2) $\frac{B q}{2 \pi r m}$
3) $\frac{2 \pi m}{B q}$
4) $\frac{B m}{2 \pi q}$

Solution:

Helical path

When the charged particle is moving at an angle to the field particle describe a path called helix.

wherein

The time period of the helical path

$T=\frac{2 \pi m}{q B}$

Hence, the answer is the option (3).

Summary

The motion of a charged particle in a uniform magnetic field results in a curved trajectory due to the Lorentz force, producing circular or helical paths. This motion underpins technologies like cyclotrons and particle accelerators and natural phenomena such as auroras. The derived equations for the radius, period, and frequency of this motion are essential for solving practical problems in physics.