Motion Of Blocks When Connected With String

When the motion of one is directly related to the motion of the other, these bodies are said to be in connected motion One end of a string that is wound around a solid body is connected to a point mass. When released, the mass descends vertically, and the solid body spins, unwinding the string.

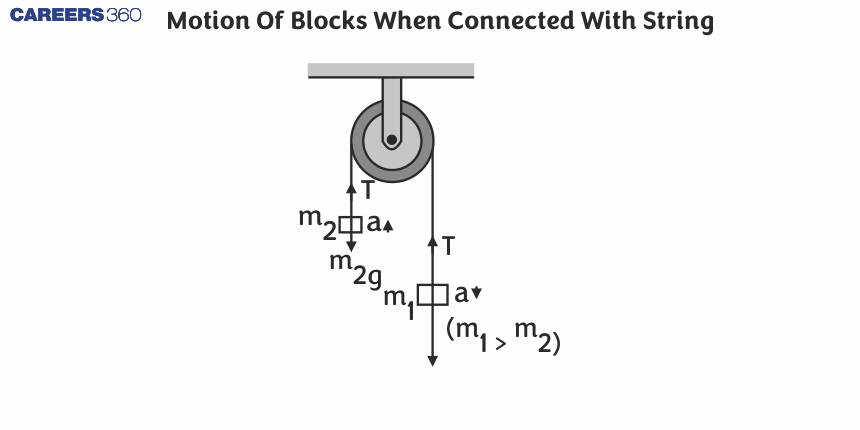
In this article, we will cover the concept of motion of blocks when connected with string. This topic falls under the broader category of laws of motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. It's an important topic for the JEE Main exam as well as the NEET exam.

Let's read this entire article to gain an in-depth understanding of the Motion of blocks when connected with string.

Two Blocks Connected With a String on a Smooth Horizontal Surface

Let acceleration of the blocks be 'a', and Tension in the string be T.

F.B.D of both blocks combined

From FBD,Fnet =MsysaF=(m1+m2)a⇒a=Fm1+m2…

F.B.D of a block of mass m₁

From Fnet =Msys aT=m1a From equation (1) ⇒T=m1Fm1+m2… (2)

Three Blocks Connected With a String on a Smooth Horizontal Surface

Let acceleration of the blocks be 'a', tension in the string between m₁ and m₂ be T₁, and tension between m₂ and m₃ be T₂.

F.B.D of all the blocks combined

From FBD, Fnet =Msys aF=(m1+m2+m3)a⇒a=Fm1+m2+m3…

F.B.D of block m₁

_{From Fnet =Msys a
T1=m1a}

_{From equation (1) -
⇒T1=m1Fm1+m2+m3…}

F.B.D of m₃

From Fnet =Msys aF−T2=m3a⇒T2=(m1+m2)Fm1+m2+m3…

Recommended Topic Video

Solved Examples Based on the Motion of Blocks When Connected With String

Example 1: Two blocks kept on the smooth horizontal surfaces of masses 7kg and 3kg connected with a light string are pulled by applying a horizontal force of 40N as shown in the figure. The tension force (in N) in the string is-

1) 28N

2) 12N

3) 21N

4) None of the above

Solution :

Given :
m1=7kg,m2=3kg,F=40N

Let acceleration of the blocks be 'a', and Tension in the string be T. F.B.D of both blocks combined-

F=(m1+m2)a⇒a=Fm1+m2a=4010=4 m/s2

F.B.D of block of mass m1

T=m1aT=7×4=28N

Hence, the answer is option (1).

Example 2: Three blocks of masses 6kg, 4kg, and 2kg kept on a smooth surface connected together with light strings are pulled applying 24N horizontal force as shown in the figure. The tension T₁ in the string is- (in N)

1) 22

2) 12

3) 10

4) 30

Solution :

Given :
m1=6kg,m2=4kg,m3=2kg,F=24 N

Let accelereration of the blocks be 'a'.
And tension in the string between m1 and m2 be T1, and tension between m2 and m3 be T2.

F.B.D of all the blocks combined-

F=(m1+m2+m3)a⇒a=Fm1+m2+m3∴a=246+4+2=2412=2 m/s2

F.B.D of block m1 :

From Newton second law of motion,
T1=m1a=6×2=12 N

Hence, the answer is option (2).

Example 3: A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force F is applied at the free end of the rope, the force exerted by the rope on the block is:

1) PmM+m
2) FM+m
3) p
4) FMM+m

Solution :

Acceleration, (a)=Fnet Total mass a=F(M+m)

FBD of Mkg block :

From Newton's 2nd laws of motion
F=Ma=M(FM+m)∴T=MFM+m

Hence, the answer is option (4).

Example 4: Three identical blocks of masses 2kg each, are kept on the smooth surface. The system is drawn by applying forces of 15N and 3N as shown in the figure. Determine the Tension T₁ (in N) in one string as shown in the figure.

1) 9

2) 8

3) 7

4) 10

Solution :

Given :
m1=m2=m3=2Kg,F1=15N,F2=3N

Let the acceleration of the combined system be 'a'.
a=Fnet Total Mass a=15−32+2+2=126=2 m/s2
F.B.D of leftmost block-

From Newton's 2nd law of motion
T1−3=2a∴T1=2×2+3=7N

Hence, the answer is option (2).

Summary

When a force F is applied vertically or horizontally to two objects connected by a string, the resultant tension in the string causes some acceleration. This phenomenon is known as connected motion. Another way to describe it is as items that move at the same speed and are connected by certain links. Attached to one end of a string that is wound around a solid body is a point mass. Unwinding the string, the solid body spins and the bulk falls vertically downward upon release.