Motion Of Bodies In Contact

The motion of bodies in contact is a fundamental concept in physics, describing how objects interact when they come into contact with one another. Whether it's a car tire gripping the road, a book sliding across a table, or two gears meshing in a machine, the principles governing these interactions are crucial in understanding the forces at play. In everyday life, these interactions determine how effectively we can walk without slipping, how vehicles maintain control on different surfaces, and even how machinery operates efficiently. By studying the motion of bodies in contact, we gain insights into friction, normal forces, and the principles that keep everything from slipping and sliding, ensuring stability and control in our daily experiences. This understanding is not just theoretical but directly applicable to engineering, safety, and technology design.

This Story also Contains

1. 1. When 2 Blocks are in Contact
2. 2. When 3 Blocks are in Contact
3. Solved Examples Based on Motion of Bodies In Contact
4. Summary

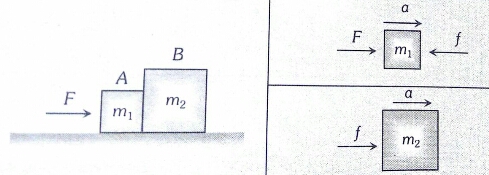
1. When 2 Blocks are in Contact

When two blocks are in contact, their motion is influenced by the forces they exert on each other. This situation is common in various mechanical systems and everyday scenarios, such as when you push a stack of books or when one block rests on another on an inclined plane. The interaction between the blocks is governed by Newton's laws of motion, particularly the third law, which states that for every action, there is an equal and opposite reaction. This means that when one block applies a force on the other, the second block applies an equal force in the opposite direction. Additionally, friction plays a significant role in determining whether the blocks will move together or slide relative to each other.

$\begin{aligned} & F-f=m_1 a \\ & f=m_2 a \\ & a=\frac{F}{m_1+m_2} \\ & f=\frac{m_2 F}{m_1+m_2}\end{aligned}$

2. When 3 Blocks are in Contact

When three blocks are in contact with one another, they form a system where the motion of each block is influenced by the forces exerted by the others. In such a scenario, the force applied to one block is transmitted through the contact points to the other blocks, creating a chain reaction of forces and motions. Understanding this system requires analyzing the forces at each contact point, such as friction, normal forces, and any external forces acting on the blocks. This analysis helps in determining the acceleration of each block, its relative motion, and the overall behaviour of the system.

$\begin{aligned} & \text { Use } F_{\text {net }}=m a \\ & a=\frac{F}{m_1+m_2+m_3} \\ & f_1=\frac{\left(m_2+m_3\right) F}{m_1+m_2+m_3} \\ & f_2=\frac{m_3 F}{m_1+m_2+m_3}\end{aligned}$

Recommended Topic Video

Solved Examples Based on Motion of Bodies In Contact

Example 1: Two blocks of masses m₁ = 5kg and m₂ = 10kg are placed in contact on the horizontal smooth surface as shown in the figure. A constant force of 150N is applied horizontally on the block m, and then the acceleration (in m/s²) of the system is :

1) 10

2) 15

3) 30

4) 35

Solution :

Given :

$
\begin{aligned}
& m_1=5 \mathrm{~kg} \\
& m_2=10 \mathrm{~kg} \\
& F=150 \mathrm{~N}
\end{aligned}
$

Let acceleration of both the blocks be 'a'

F.B.D of both blocks combined

From Newton's 2nd law of motion,

$
\begin{aligned}
& F=\left(m_1+m_2\right) a \\
& \therefore a=\frac{F}{m_1+m_2}=\frac{150}{15}=10 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$

Hence the answer is the option (1).

Example 2: Three blocks m₁= 1kg, m₂ = 1.5kg and m₃ = 2kg are in contact with each other on a frictionless surface as shown in the figure. What will be the contact force between m₂ and m₃ if the value of F is 18N?

1) 10N

2) 8N

3) 6N

4) 12N

Solution :

Given :

$
\begin{aligned}
& m_1=1 \mathrm{~kg} \\
& m_2=1.5 \mathrm{~kg} \\
& m_3=2 \mathrm{~kg} \\
& F=18 \mathrm{~N}
\end{aligned}
$
Let the common acceleration of all the blocks be 'a'

F.B.D of all the blocks combined

From Newton's 2nd law-

$
\begin{aligned}
& a=\frac{F}{m_1+m_2+m_3} \\
& \Rightarrow a=\frac{18}{1+1.5+2}=4 \mathrm{~m} / \mathrm{s}^2 \text { Let normal reaction betweeen the blocks of mass } 1.5 \mathrm{~kg} \text { and } 2 \mathrm{~kg} \text { be 'N'. }
\end{aligned}
$

$\begin{aligned} & N=m_3 a=2 \times 4 \\ & \therefore N=8 N\end{aligned}$

Hence the answer is the option (2).

Example 3:

Given in the figure are two blocks A and B of weight 20 N and 100 N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force (in N) applied by the wall on block B is :

1) 120

2) 80

3) 100

4) 150

Solution :

Given :
Weights of blocs $\mathrm{A}=20 \mathrm{~N}$
Weight of block $B=100 \mathrm{~N}$
As the blocks are at rest, both blocks must be in equilibrium.
Let the Friction force between the blocks be $f_1$ and between block B and wall be $f_2$
F.B.D of the blocks :

From F.B.D,

$
\begin{aligned}
& F=N \\
& f_1=20 \\
& f_2=f_1+100 \\
& \Rightarrow f_2=20+100=120 N
\end{aligned}
$

Hence the answer is the option (1).

Example 4: A horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is (in N):

1) 2

2) 50

3) 100

4) 20

Solution :

Given :
Horizontal force $(\mathrm{F})=10 \mathrm{~N}$ coefficient of friction between block and wall, $(\mu)=0.2$

Applying Newton's Second Law

$
\begin{aligned}
& \sum F_x=0 \\
& N-10=0 \\
& \therefore N=10 N
\end{aligned}
$
$
\begin{aligned}
& \text { And, } \sum F_y=0 \\
& f-W=0 \\
& \Rightarrow f=W=\mu N=0.2 \times 10 \\
& \therefore W=2 N
\end{aligned}
$

Hence the answer is the option (1).

Example 5: A block of mass m is connected to another block of mass M by a spring ( massless ) of spring constant K. The blocks are kept on a smooth horizontal plane. Initially, the blocks are at rest and the spring is unstretched Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass m.

1) $\frac{M F}{(m+M)}$
2) $\frac{m F}{M}$
3) $\frac{(M+m) F}{m}$
4) $\frac{m F}{(m+M)}$

Solution:

When 2 Blocks are in Contact

$
\begin{aligned}
& F-f=m_1 a \\
& f=m_2 a
\end{aligned}
$

wherein

$
\begin{aligned}
& a=\frac{F}{m_1+m_2} \\
& f=\frac{m_2 F}{m_1+m_2}
\end{aligned}
$

: Acceleration of the system $a=\frac{F}{m+M}$
Force on block of mass $m=m a=\frac{m F}{m+M}$

Hence the answer is the option (4).

Summary

The motion of bodies in contact involves analyzing the forces and interactions between objects when they touch. Whether dealing with two or three blocks in contact, these interactions are governed by Newton's laws of motion, friction, and normal forces. By solving related problems, one can determine the resulting accelerations, contact forces, and the effects of friction, which are essential for understanding various mechanical systems and real-world applications.