Motion Of Two Bodies One Resting On The Other

To understand the motion of two bodies one resting on the other it as simply as possible, imagine you have put a book on top of a skateboard and given it a little nudge. While that skateboard is moving, the book is moving with the skateboard. These simple physical actions are supposed to involve a very interesting concept of motion and friction, which is quite in use in everyday life. The interaction of the two bodies, one resting on the other, helps us understand the dynamics of how the forces work together to create the motion.

In this article, we shall find out what happens when two bodies interact where one is at rest over the other one. This concept falls under the broader category of Laws of motion which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question has been asked on this concept. And for NEET no direct questions were asked from this concept.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Block on Block Problems
2. When Force F is Applied to the Lower Body
3. Solved Example Based On Motion Of Two Bodies One Resting On The Other
4. Summary

Block on Block Problems

Let us assume two blocks of masses m_1, and m₂ are kept on a smooth horizontal surface as shown in the figure. The coefficient of friction between the blocks is μ. As the block of mass m₁ is being fulled by applying force F the system starts moving.

To solve problems based on block-on-block situations, we must begin by calculating the limiting friction at all the rough surfaces. These values will help us determine the possibilities of relative motion between bodies in contact. As the surface is smooth block m₁ will begin to move for any value of F. However the friction between the blocks will try to stop any relative motion between the blocks. Therefore, the friction force between the blocks will take any suitable direction and magnitude such that both blocks move with the same acceleration (no relative motion). In this case, the friction force between the blocks will be of static type. However, if we increase the value F, the requirement of friction force for no relative motion will also increase. The value of friction force can not be greater than the limiting value of friction.

To solve such problems we will initially assume that friction has successfully ensured that there is no relative motion between the blocks an determine the value of frictional force for such conditions. If this value of frictional force is less than the limiting friction, we can say that our assumption was right and all the results thus determined are the correct results.

But, if the value of frictional force comes to be more than limiting friction assuming no relative motion, then we know our assumption was incorrect as the value of friction force can not be greater than limiting friction. In such a case, since we have established that there is a relative motion between the blocks we must apply kinetic friction in a suitable direction and determine different accelerations of the blocks.

Let us first assume that there is no relative motion between the blocks. Both the blocks are moving with common acceleration a_c and the friction force between the blocks is f.

F.B.D of both blocks m_1, and m₂ together-

F=(m1+m2)acac=Fm1+m2

F.B.D of the block of mass m_2-

N=m2 g

Limiting friction-
fl=μN=μm2 g

From newton's law-
f=m2ac=m2 F m1+m2

Case-1
f≤fl or m2 F m1+m2≤μm2 g

If this is the case then our assumption is correct and the blocks will move together with acceleration a_c and the friction force between them is static and equal to f. Where-

ac=Fm1+m2f=m2 F m1+m2

Case-2
f>fl or m2 F m1+m2>μm2 g

If this is the case, then our assumption is wrong as static friction can not be greater than limiting friction. In this case the the friction force acting between the blocks will be kinetic friction and both blocks will move with different accelerations. Let us assume the accelerations of blocks m₁ , and m₂ be a_1, and a₂ respectively.

Kinetic friction-
fk=μN=μm2 g

Along horizontal direction-
F−fk=m1a1a1=F−μm2 g m1fk=m2a2a2=μg

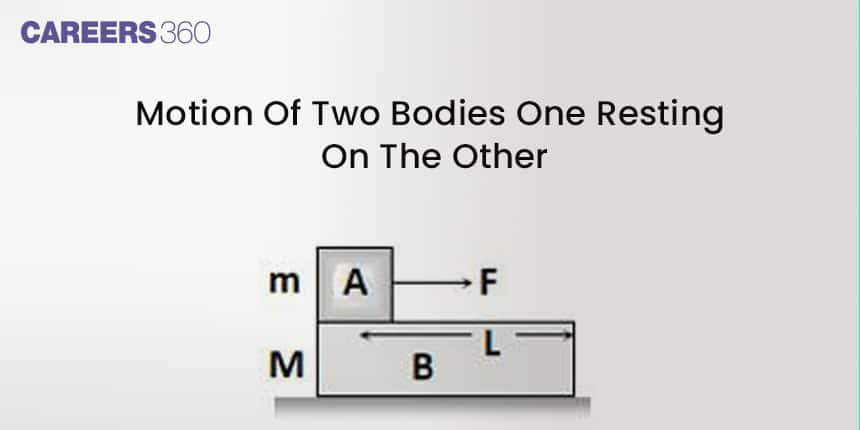
Now, coming to the second part, when force is applied to the lower body.

When Force F is Applied to the Lower Body

Let's discuss possible 4 situations under this case:-

• When there is no friction:-

B will move with acceleration (F/M) while A will remain at rest (relative to ground) as there is no pulling force on A.

aB=FM and aA=0

As relative to B, A will move backwards with acceleration (F/M) and so will fall from it in time t,

t=2La=2MLF

• If friction is present between A and B only and

F' (Pseudo force on body A) < F_l (limiting friction between body A and B):-

Both the bodies will move together with common acceleration, which is given by a=Fm+M

And the value of F' will be

F′=ma=Fm+M=mFm+M and Fl=μsmg as F′<Fl⇒mFm+M<μsmg⇒F<μs(m+M))g

So both bodies will move together with acceleration,

aA=aB=Fm+M if F<μs(m+M))g

• If friction is present between A and B only and F > F'_l(limiting friction between body A and B):-

Fl′=μs(m+M))g

Both the bodies will move with different accelerations. Here force of kinetic friction μkmg will oppose the motion of B while will cause the motion of A.

maA=μkmg i.e aA=ukg

similarly,

F−Fk=MaB i.e. aB=[F−μkmg]M

As both, bodies are moving in the same direction,

Acceleration of body A relative to B will be given by:-

a=a_A-a_B=-\left[\frac{F-\mu_k g(m+M)}{M}\right]

A negative sign implies that relative to B, A will move backwards and will fall it after time,

t=2La=2MLF−μkg(m+M)

• If there is friction between B and floor and F>F_l (limiting friction between body B and surface):-

Here Fl′′=μs(m+M)g

The system will move only if F>F_l then replacing F by

The entire situation (3) will be valid. However if

F<Fl′′,

The system will not move. This means friction between B and the floor will be F while between A and B is zero.

Recommended Topic Video

Solved Example Based On Motion Of Two Bodies One Resting On The Other

Example 1: Find the maximum value of F (in N) such that both blocks move together, given coefficient of friction between two blocks is 0.2 and the lower block is placed on a smooth surface. Take (g=10m/s²)

1)15

2)20

3)30

4)10

Solution:

As we keep on increasing the value of F, the value of friction force between blocks will also increase so as to stop relative motion between the blocks. for a maximum value of F, the friction force will also be maximum (Limiting friction).

let the common acceleration of blocks be a_c, and limiting friction between the blocks be f_l.

F.B.D of both blocks combined-

F=15ac…(1)

F.B.D of 5 kg block:

N=50fll=μN=0.2×50=10 N F−fl=5acF=10+5ac…(2)

From equation (1) and (2)-

F=15 N

Hence, the correct answer is option (1).

Example 2: The arrangement of the block system is shown in the figure. mass of block A is mA=5 kg and mass of B is mB= 10 kg. A constant force F = 100 N is applied on upper block A . Friction between A and B is μ and b/w B and the ground surface is smooth, then find the displacement (in meters) of block B in t = 2 sec if the system starts from rest.

1)5

2)4

3)3

4)8

Solution:

So draw FBD

For block A,N=mg and fK=μN
⇒μmg=μMng=0.5×5×10=25NfK=mBa=μmAg⇒a=μmAmB

For block B,
=0.5×5×1010=2.5 m/s2s=μt+1/2at2⇒s=1/2×2.5×4=5 m

Example 3: A block of mass 5kg and negligible dimensions are kept at the right edge of a plank of length 50cm and mass 10kg, as shown in the figure. The coefficient of friction between the plank and block is 0.5 and the ground is smooth. If the plank is being pulled with a force of 85N, the time taken for the block to fall over the plank is-

(g=10m/s² )

1)1.25 sec

2)0.75 sec

3)1 sec

4)Never

Solution:

Masse of block₌5kg

Mass of the plank=10 kg

Coefficient of friction between blocks, μ=0.5.

Length of Plank l=50 cm=0.5m

Only friction force is responsible for the motion of the block of mass 5 kg.

First, we need to check whether the block and the plank are moving together or separately for the given force of 85 N. For that, we will first assume the block and the plank are moving together with common acceleration a_c. Then, we will determine the maximum possible acceleration a_max of the block (when limiting friction is acting on the block). If a_max is less than a_c, then our assumption is right otherwise block and plank are moving separately.

F.B.D of block and plank combined-

Fnet =msys a85=15acac=5.67 m/s2

F.B.D of the block-

N=50fl=μN=25 Nfl=5amaxamax=5 m/s2

Since, amax<ac

Both block and plank are moving separately. Therefore, Friction acting between the blocks will be kinetic.

Kinetic friction-

fk=μN=25 N

Let the acceleration of the plank be a₁ and, the acceleration of the block be a_2.

F.B.D of the block and the plank-

For, 5 kg block-
fk=5a2a2=5 m/s2

For 10 kg plank-
85−fk=10a1a1=6 m/s2

In the frame of reference of the plank-
Acceleration of block with respect to plank-
a21=a2−a1=−1 m/s2

Displacement of block before jumping off the planks21=−0.5 m

Let the time taken be 't' sec.

From second equation of motion -

s21=u21t+12a12t2−0.5=−0.5t2t=1sec

Hence, the answer is option (3).

amax=μg=37×9.8 F=(M+m)amax=5amax=21 Newton

Summary

In this article, we shall find out what happens when two bodies interact where one is at rest over the other one. We shall first look into how the friction between the two surfaces affects the motion of the two. In addition, we shall discuss the forces acting on both bodies, which include the normal and frictional forces. Further, we look at conditions under which the upper body is bound to slide and the impact of different surfaces and forces in such an instance. At the conclusion of this article, you should clearly understand the governing principles regarding the motion of two bodies in contact.