Mu Naught Value - Definition, Unit, Types, FAQs

Magnetic permeability is a fundamental property of materials that describes how easily they get magnetized when subjected to a magnetic field. To describe the magnetic properties of a given substance, we require some quantities, which include a quantity called magnetic permeability, denoted as $\mu$, which is pronounced as the "mew" symbol or "mu" or "meu" sign. Hence, in magnetism, mu means magnetic permeability. It quantifies the ability of a material to support the formation of the magnetic field within itself. In this article, we will come across three types of magnetic permeability. Also, we will learn about topics like basic principles, mathematical descriptions, and factors affecting magnetic permeability in this article.

This Story also Contains

1. Magnetic Permeability Definition
2. Relation Between $\mu$, B, and H
3. Units and Dimensions of Magnetic Permeability
4. Types of Magnetic Permeability
5. Value of $\mu_r$ (Relative Permeability) for Different Types of Materials
6. Magnetic permeability of some standard materials
7. Relationship Between Magnetic Permeability $\mu_r$ and Magnetic Susceptibility ($\chi_m$)
8. Factors Affecting Magnetic Permeability
9. Applications Of Magnetic Permeability In Technology

Magnetic Permeability Definition

Magnetic permeability ($\mu$) is the ability to measure the degree of penetration of the magnetic field through the medium. It also measures the capacity of the substance to take on magnetism. However, to define magnetic permeability, we must know about magnetic field strength/magnetic induction, denoted by ‘B’, and magnetic field intensity, denoted by ‘H’.

• Magnetic intensity (H) is the degree to which a magnetic field can magnetize a material. S.I. unit of H is Ampere/meter (A/m)
• It can also be measured in oersted. Note: 1 A/m is equal to 0.012566 oersted.
• Magnetic induction (B), also called magnetic flux density, is the force experienced by a unit positive charge moving with a velocity perpendicular to the magnetic field. This definition of B has come from the formula of Lorentz force.
• The S.I. unit of B is Tesla or Weber/$m^{2}$, and the C.G.S. unit is Gauss (G), where 1G=$10^{-4}$ T.

Relation Between $\mu$, B, and H

We know that B∝H

B=$\mu$H, where $\mu$ is the constant of proportionality and stands for magnetic permeability.

Thus, we can define magnetic permeability as the ratio of magnetic field induction (B) to the magnetic intensity (H).

$\mu$=BH

where,

$\mu$ is the permeability

B is the magnetic flux density

H is the magnetic field strength

Units and Dimensions of Magnetic Permeability

• The S.I. unit of $\mu$

The unit for magnetic permeability is Wb$A^{-1}$ $m^{-1}$

Given

B =Wb/$m^{2}$

H = A/m

The unit of magnetic permeability is

$\mu$=B/H

Unit of $\mu$ =Wb/$m^{2}$ .m/A

simplifying

Unit of $\mu$=Wb$A^{-1}$$m^{-1}$

• Another unit is Henry per meter ( H/m ).

B=T (Tesla)

H=A/m (Ampere per meter)

Now, the unit of $\mu$ (magnetic permeability) is

$\mu$=T.m/A

$\mu$=kg⋅ $s^{-2}$⋅$A^{-1}$.m/A
So, the unit of $\mu$ is

$\mu$=H/m

• Another unit of $\mu$ is Newton per ampere square (N⋅$A^{-2}$) or Tesla meter per ampere (T⋅m⋅$^A{-1}$).

B=T (Tesla)

H=A/m (Ampere per meter)

Now the unit of $\mu$ = T⋅m$A^{-1}$

or
Unit of $\mu$=T⋅m$A^{-1}$
Unit of $\mu$= N A⋅ m
Unit of $\mu$= N $A^{-2}$

Dimensional Formula For Magnetic Permeability In Free Space

The magnetic permeability in free space $\mu_0$ = 4π×$10^{-7} $H/m
Dimensional formula:

1 H = 1 kg⋅ $m^{2}$$s^{-2}$⋅ $A^{-2}$
We know that,

$\mu_0$=1H/m

⇒$\mu_0$ = 1 kg⋅ $m^{2}$ $s^{-2}$⋅ $A^{-2}$$m^{-1}$

⇒$\mu_0$ = kg⋅ m⋅ $s^{-2}$⋅ $A^{-2}$

The dimensional formula of magnetic permeability of free space,

Dimensional formula of $\mu_0$ = $\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$

Types of Magnetic Permeability

We will come across three types of magnetic permeability, i.e., magnetic permeability in a vacuum ($\mu_0$) or permeability of free space, the magnetic permeability of a medium ($\mu$), and relative magnetic permeability ($\mu_r$).

• Magnetic permeability of free space ($\mu_0$): It is the ratio of magnetic induction in free space to magnetic intensity,

i.e., $B_o$=$\mu_0$H⇒$\mu_0$=$B_o$H

The value of $\mu_0$ = 4π × $10^{-7}$ Wb $A^{-1}$ $m^{-1}$

• Permeability of medium ($\mu$): It is the ratio of magnetic field induction in the medium to the magnetic intensity.

$\mu$=BH

• Relative permeability ($\mu_r$): It is defined as the ratio of the magnetic permeability of a medium to the magnetic permeability of free space or vacuum.

$\mu_r$=$\mu$/$\mu_0$

Relative permeability of a material can also be defined as the ratio of the number of magnetic field lines per unit area (flux density, i.e., B) in that material to the number of magnetic field lines per unit area that would be present if the material is replaced by a vacuum (flux density in a vacuum, i.e., $B_o$).

As both the quantities involved in the above equations have the same unit, relative permeability has no units and is a dimensionless quantity. It is just a number.

Value of $\mu_r$ (Relative Permeability) for Different Types of Materials

Based on magnetic properties, Faraday classified materials into three categories. These are

1. Diamagnetic materials

2. Paramagnetic materials

3. Ferromagnetic materials

Let us briefly understand each of these based on their $\mu$ values.

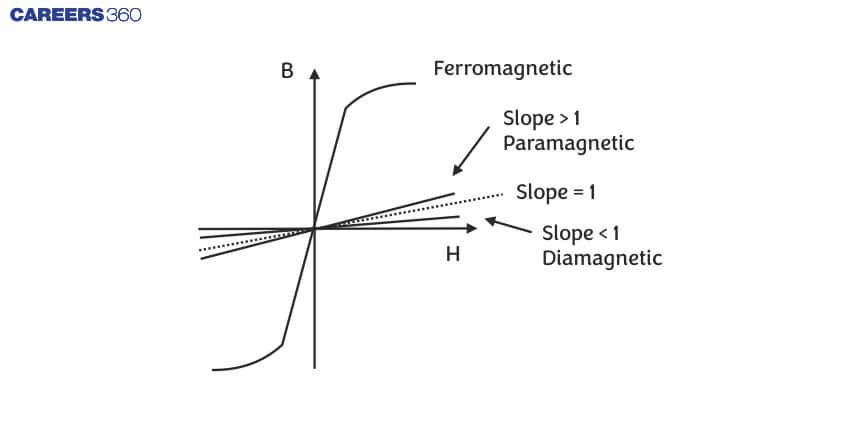
Diamagnetic materials

• These materials have atoms that don’t possess their magnetic moment.
• When these materials are placed in an externally applied field, they get slightly magnetized, and that too in the opposite direction to the applied magnetic field.
• Examples are- diamond, bismuth, gold, silver, copper, water, mercury, alcohol, nitrogen, hydrogen, including all inert gases, etc.

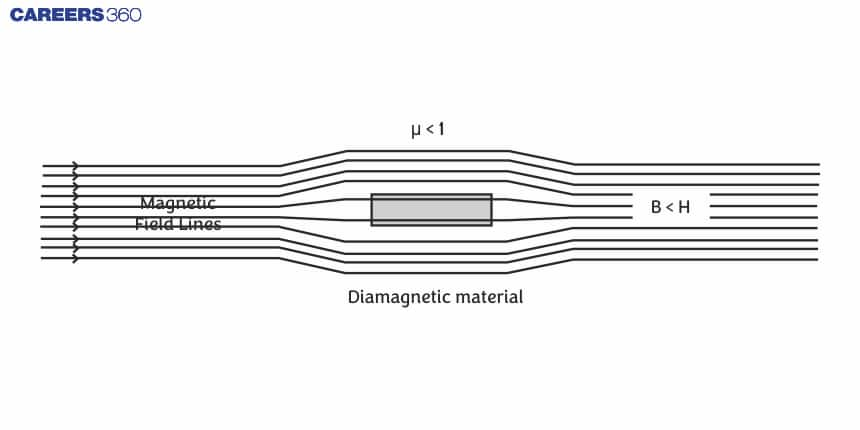
• When we place a diamagnetic specimen in a magnetizing field, the field lines do not prefer to pass through the specimen material.

Hence, $\mu_r$= negative, and it is less than 1.

This is because,

B<$B_o$⇒B/$B_o$<1

$\mu_r$<1 (The relative permeability value for diamagnets is always less than 1.)

Paramagnetic materials

• These materials have non-zero net magnetic moments of their own.
• When they are placed in an externally applied magnetic field, they get magnetized in the same direction as the applied magnetic field.
• In the absence of an external magnetic field, paramagnets do not behave like magnets. The reason behind this is that their net magnetic moment per unit volume becomes equal to zero because of the random arrangement of their magnetic moments of atoms.
• Examples are tungsten, oxygen, sodium, aluminum, chromium, manganese, lithium, magnesium, potassium, platinum, etc.

• In the case of paramagnetic materials, the magnetic field lines prefer to pass through the specimen rather than through the air.

Thus, B>$B_o$⇒B/$B_o$>1

$\mu_r$>1 ( $\mu_r$ values for paramagnetic are always greater than 1).

Ferromagnetic materials

• These materials have their permanent magnetic moment like that of paramagnetic materials.
• When they are placed in an external magnetic field, they get strongly magnetized in the direction of the applied external magnetic field. Hence, they start behaving as magnets even if the external magnetic field is removed or not present.
• Examples are- iron, cobalt, nickel, gadolinium, and other alloys

• Ferromagnetic materials show all the properties of paramagnetic materials, but in a better way and to a much greater degree.

Thus, the $\mu$_r value is very high in these materials, i.e., $\mu_r$=$10^3$ to $10^5$.

Note: there is a B-H graph, or hysterisis curve, for all magnetic materials discussed above, the slope of which gives us the curve’s incremental permeability. Hysteresis loops are also plotted in the B-H graph for ferromagnetic materials. The B-H graph for all three magnetic materials is given below.

Magnetic permeability of some standard materials

Relationship Between Magnetic Permeability $\mu_r$ and Magnetic Susceptibility ($\chi_m$)

• Magnetic susceptibility is a property of a substance that tells us how easily a material can be magnetized when it is placed in an external magnetic field. It is denoted by $\chi_m$ (pronounced as chi).
• It is defined as the ratio of the intensity of magnetization to magnetic intensity

$\chi_m$=IH

• It has no units, as both I and H have the same units.

Now, when a magnetic material is placed in an external magnetic field of magnetic intensity H, it gets magnetized.

Then, the total magnetic field induction is

B=$B_o$+B_m
Therefore,

B=$\mu$₀(H+I)
We know that,

I=$\chi_m$H
Therefore, putting this value in equation (1):

B=$\mu_0$H($\chi_m$+1)
But,

B=$\mu$H

⇒$\mu$H=$\mu_0$H($\chi_m$+1)

⇒$\mu$/$\mu_0$=$\chi_m$+1

⇒$\mu_r$=$\chi_m$+1

Factors Affecting Magnetic Permeability

• Temperature
• Magnetic Field Strength
• Material Composition
• Position in the medium
• Frequency of the Magnetic Field
• Humidity

Applications Of Magnetic Permeability In Technology

• Used in Transformers and Inductors: Materials with high magnetic permeability are used in the cores of transformers and inductors to improve their efficiency.
• Electric Motors and Generators: The materials with high relative magnetic permeability increase magnetic field interaction and energy conversion. Thus, they can be used in the cores of motors and generators.
• Sensors and Instruments: Magnetic field sensors, fluxgate magnetometers, and MRI machines use materials with specific magnetic permeability for better efficiency

Also read:

• NCERT Exemplar Solutions for All Subjects
• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects