Multiplication Of Vectors

Vector multiplication can be divided into two categories. A vector has both a magnitude and a direction, and as a result, the dot product of two vectors and the cross product of two vectors are the two methods of multiplying vectors.

Let us study the two-way multiplication of vectors, including the working rule, properties, applications, and examples of this type of multiplication. which belongs to the chapter Kinematics, which is an important chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), more than ten questions have been asked on this concept. And for NEET one questions were asked from this concept.

Types of Vector

Let's start with the types of vectors.

Unit Vector

A vector having a magnitude of one unit is called a unit vector. It is represented by a cap/hat over the letter.

$\mathrm{Eg}-\hat{R}$ is called a unit vector of $\vec{R}$. Its direction is along the $\vec{R}$ and magnitude is unit.

Unit vector along $\vec{R}$ -
$
\hat{R}=\frac{\vec{R}}{|\vec{R}|}
$

Orthogonal Unit Vectors

It is defined as the unit vectors described under the three-dimensional coordinate system along the x, y, and z-axis. The three unit vectors are denoted by i, j and k respectively.

Any vector (Let us say $\vec{R}$ ) can be written as
$
\vec{R}=x \hat{i}+y \hat{j}+z \hat{k}
$

$\text { Where } \mathrm{x}, \mathrm{y} \text { and } \mathrm{z} \text { are components of } \vec{R} \text { along } \mathrm{x}, \mathrm{y} \text { and } \mathrm{z} \text { direction respectively. }$

$|\vec{R}|=\sqrt{x^2+y^2+z^2}$

Unit vector

$\hat{R}=\frac{x \hat{i}+y \hat{j}+z \hat{k}}{\sqrt{x^2+y^2+z^2}}$

1. If a vector is multiplied by any scalar

$\vec{Z}=n \cdot \vec{Y}$

(n=1,2,3..)

$\text { Vector } \times \text { Scalar }=\text { Vector }$

We get again a vector.

If a vector is multiplied by any real number (eg 2 or -2) then again, we get a vector quantity.

E.g.

• $\text { If } \vec{A}$ is multiplied by 2 then the direction of the resultant vector is the same as that of the given vector.

$\text { Vector }=2 \vec{A}$

• $\text { If } \vec{A}$ is multiplied by (-2), then the direction of the resultant is opposite to that of the given vector.

$\text { Vector }=-2 \vec{A}$

Scalar or Dot or Inner Product

• Scalar product of two vectors $\vec{A} \& \vec{B} \text { written as } \vec{A} \cdot \vec{B}$

• $\vec{A} \cdot \vec{B}$ is a scalar quantity given by the product of the magnitude of $\vec{A} \& \vec{B}$ and the cosine of a smaller angle between them.

$\vec{A} \cdot \vec{B}=A B \cdot \cos \Theta $

Figure showing the representation of scalar products of vectors.

Important results-

$\begin{aligned}
& \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 \\
& \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1 \\
& \vec{A} \cdot \vec{B}=\vec{B} \cdot \vec{A}
\end{aligned}$

Vector or Cross-Product

• Vector or cross product of two vectors $ \vec{A} \& \vec{B} \text { written as } \vec{A} \times \vec{B}$

• $A \times B$ is a single vector whose magnitude is equal to the product of the magnitude of $\vec{A} \& \vec{B}$ and the sine of the smaller angle $\theta$ between them.

• $\vec{A} \times \vec{B}=A B \sin \theta$

The figure shows the representation of the cross-product of vectors.

Important results

$ \begin{aligned}
& \quad \hat{i} \times \hat{j}=\hat{k}, \hat{j} \times \hat{k}=\hat{i}, \hat{k} \times \hat{i}=\hat{j} \\
& \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{0} \\
& \vec{A} \times \vec{B}=-\vec{B} \times \vec{A}
\end{aligned}$

Recommended Topic Video

Solved Example Based on Multiplication of Vector

Example 1: When we multiply a vector $\vec{A}=2 \hat{i}+3 \hat{j}-5 \hat{k}$ with a number -2, we get

1) A scalar with a magnitude same as that of the vector

2) A vector with the same magnitude and opposite direction.

3) A vector with double magnitude and opposite direction.

4) A vector with double magnitude and the same direction

Solution:

$\text { If } \vec{A}$ is multiplied by (-2), then the direction of the resultant is opposite to that of the given vector.

$\begin{aligned}
& \text { Vector }=-2 \vec{A} \\
& \vec{B}=-2 \cdot \vec{A}=2(-\vec{A})
\end{aligned}$

The direction of $\vec{B} \text { is opposite of } \vec{A}$ and

Magnitude of $ |\vec{B}|=2 \times \text { magnitude of }|\vec{A}| $.

Hence, the answer is the option (3).

Example 2: Let $\vec{A}=(\hat{i}+\hat{j})$ and, $\vec{B}=(2 \hat{i}-\hat{j})$ The magnitude of a coplanar vector $\vec{C}$ such that $\vec{A} \cdot \vec{C}=\vec{B} \cdot \vec{C}=\vec{A} \cdot \vec{B}$ is given by:

1) $\sqrt{(10 / 9)}$
2) $\sqrt{5 / 9}$
3) $\sqrt{(20 / 9)}$
4) $\sqrt{(9 / 12)}$

Solution:

$\begin{aligned}
& \text { Let } \vec{c}=x \hat{i}+y \hat{j} \\
& \begin{array}{l}
\vec{A} \cdot \vec{C}=x+y \\
\vec{B} \cdot \vec{C}=2 x-y \\
\vec{A} \cdot \vec{B}=2-1=1 \\
\Rightarrow x+y=1 \\
2 x-y=1
\end{array}
\end{aligned}$

$\begin{aligned}
& 3 x=2 \quad \text { or } \mathrm{x}=2 / 3 \\
& \mathrm{y}=1 / 3 \\
& \therefore \vec{c}=2 / 3 \hat{i}+1 / 3 \hat{j} \\
& \therefore|\vec{c}|=\sqrt{(4 / 9+1 / 9)}=\sqrt{(5 / 9)}
\end{aligned}$

Hence, the answer is the option (2).

$\text { Example 3: The angle between }(\hat{l}+\hat{j}) \text { and }(\hat{l}-\hat{j}) \text { is (in degrees) }$

1) 90

2) 60

3) 45

4) 30

Solution:

As we learned

Scalar, Dot or Inner Product -

The scalar product of two vectors $\vec{A} \& \vec{B}$ written as $\vec{A} \cdot \vec{B}$ is a scalar quantity given by the product of the magnitude of $\vec{A} \& \vec{B}$ and the cosine of the smaller angle between them.

$\vec{A} \cdot \vec{B}=A B \cdot \cos \Theta$

- wherein

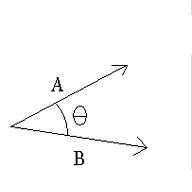
showing a representation of scalar products of vectors.

$\begin{aligned}
& (\hat{l}+\hat{j}) \cdot(\hat{l}-\hat{j})=|\hat{l}+\hat{j}||\hat{l}-\hat{j}| \cdot \cos \theta \\
& U \operatorname{sing} \vec{A} \cdot \vec{B}=A B \cos \theta \\
& \Rightarrow \cos \theta=\frac{(\hat{l}+\hat{j}) \cdot(\hat{l}-\hat{j})}{|\hat{l}+\hat{j}||\hat{l}-\hat{j}|}=\frac{0}{\sqrt{2} \cdot \sqrt{2}}=0 \\
& \therefore \theta=90^{\circ}
\end{aligned}$

Hence, the answer is option (1).

Example 4: A particle is thrown with $10 \mathrm{~m} / \mathrm{s}$ at an angle of $60^{\circ}$ with horizontal the time at which its velocity is perpendicular to the initial velocity is ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}$ )

1) $\sqrt{3} \mathrm{sec}$
2) $2 \sqrt{3} \mathrm{sec}$
3) $\frac{2}{\sqrt{3}} \mathrm{sec}$
4) $\frac{4}{\sqrt{3}} \mathrm{sec}$

Solution:

$\vec{A} \cdot \vec{B}=A B \cdot \cos \Theta$

Showing the representation of scalar products of vectors.

$
\begin{aligned}
& u=10 \cos 60^{\circ} \hat{i}+10 \sin 60^{\circ} \hat{j} \\
& =5(\hat{i}+\sqrt{3} \hat{j}) \\
& V_y=u_y-g t=5 \sqrt{3}-10 t(\text { here use } g=10) \\
& \vec{V}=5 \hat{i}+(5 \sqrt{3}-10 t) \hat{j}
\end{aligned}
$
since $\vec{V}$ is perpendicular to $\vec{u} h$ ence $\vec{u} \cdot \vec{V}=0$
$
\begin{aligned}
& \Rightarrow 5(\hat{i}+\sqrt{3} \hat{j}) \cdot 5(\hat{i}+(\sqrt{3}-2 t) \hat{j})=0 \\
& \Rightarrow 1+\sqrt{3}(\sqrt{3}-2 t)=0
\end{aligned}
$
or $1+3-2 \sqrt{3} t=0$
$
\Rightarrow t=\frac{2}{\sqrt{3}} \sec
$

Hence, the answer is option (3).

Example 5: If $\vec{a}, \vec{b}$ are unit vectors such that the angle between $\vec{a}$ and $\vec{b}$ is -

1) 0
2) $\frac{\pi}{2}$
3) $\pi$
4) Indeterminate

Solution:

$\vec{A} \times \vec{B}=A B \sin \theta$

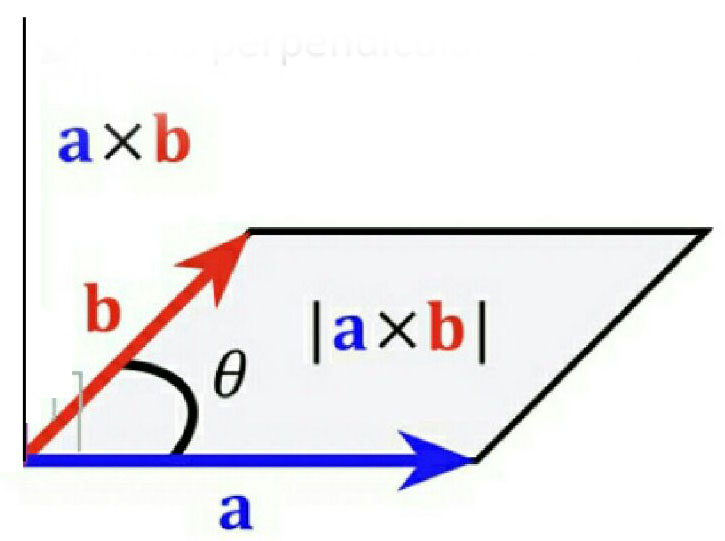
The figure shows the representation of vectors or cross product of vectors.

shows the representation of vector or cross product of vectors

$\begin{aligned}
& 0=(\vec{a}+\vec{b}) \cdot(2 \vec{a}+3 \vec{b}) \times(3 \vec{a}-2 \vec{b})=0 \\
& 0=(\vec{a}+\vec{b}) \cdot(-4 \vec{a} \times \vec{b}-9 \vec{a} \times \vec{b})=-13 \cdot(\vec{a}+\vec{b}) \cdot(\vec{a} \times \vec{b})
\end{aligned}$

which is true for all values of $\vec{a} \text { and } \vec{b}$

Summary

Vector multiplication can be divided into two categories. A vector has both a magnitude and a direction, and as a result, the dot product of two vectors and the cross product of two vectors are the two methods of multiplying vectors. Because the resultant value is a scalar quantity, the dot product of two vectors is often referred to as the scalar product of two vectors. A vector has both a magnitude and a direction associated with it.