Orbital Velocity

Orbital velocity refers to the speed at which an object must travel to remain in a stable orbit around a celestial body, such as Earth. This fundamental concept in physics and space science is crucial for understanding how satellites, space stations, and spacecraft navigate the cosmos. When an object achieves orbital velocity, it counteracts the pull of gravity by continuously falling toward the planet while moving forward, effectively balancing its trajectory. This principle is not only pivotal for launching satellites that provide crucial communication and weather data but also for ambitious space missions exploring our solar system. In everyday life, the technology and principles derived from orbital velocity enhance our global positioning systems, and satellite TV, and even contribute to scientific research that drives advancements in technology and exploration.

What is Orbital Velocity?

Orbital velocity is the speed at which an object must travel to remain in a stable orbit around a celestial body, such as a planet or star. For an object to achieve this velocity, it must balance the gravitational pull of the body it is orbiting with its own forward motion. Essentially, the object is in constant free-fall towards the celestial body but moving forward fast enough that the curvature of its path matches the curvature of the body’s surface.

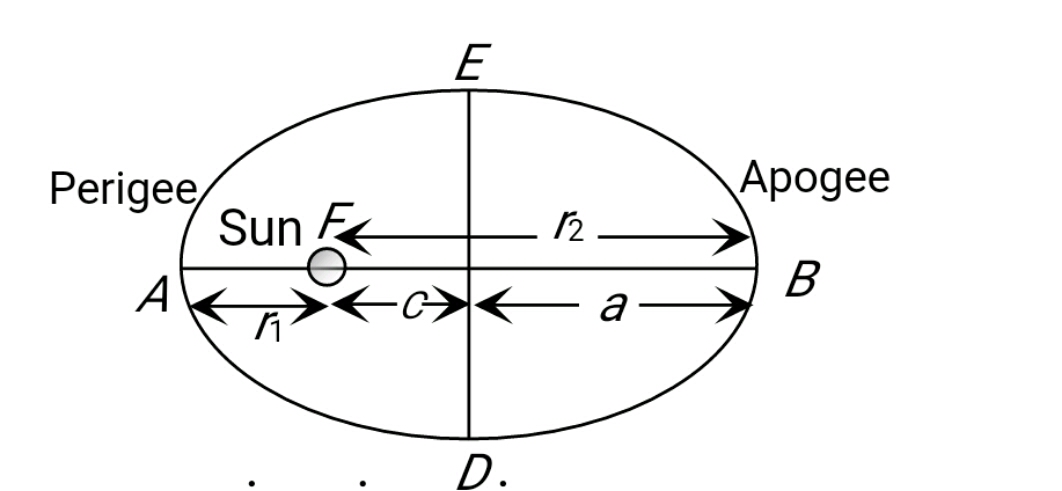
For the figure below

$
\begin{aligned}
& r_1=r_p=a-c \\
& r_2=r_a=a+c
\end{aligned}
$
If Eccentricity is given by

$
\text { (e) }=\frac{c}{a}
$

then The velocity of the planet at Apogee and Perigee in terms of Eccentricity is given by

$
\begin{aligned}
V_a & =\sqrt{\frac{G M}{a}\left(\frac{1-e}{1+e}\right)} \\
V_p & =\sqrt{\frac{G M}{a}\left(\frac{1+e}{1-e}\right)} \\
V_A & =\text { The velocity of the planet at apogee } \\
V_p & =\text { Velocity of perigee }
\end{aligned}
$

Proof

Let the mass of the sun be M and the mass of the planet be m

Applying the law of conservation of angular momentum at perigee and apogee about the sun
$
\begin{aligned}
& m v_p r_p=m v_a r_a \\
\Rightarrow & \frac{v_p}{v_a}=\frac{r_a}{r_p}=\frac{a+c}{a-c}=\frac{1+e}{1-e}
\end{aligned}
$
Applying the conservation of mechanical energy at perigee and apogee

$
\begin{aligned}
& \frac{1}{2} m v_p^2-\frac{G M m}{r_p}=\frac{1}{2} m v_a^2-\frac{G M m}{r_a} \Rightarrow v_p^2-v_a^2=2 G M\left[\frac{1}{r_p}-\frac{1}{r_a}\right] \\
\Rightarrow \quad & v_a^2\left[\frac{r_a^2-r_2^2}{r_p^2}\right]^2=2 G M\left[\frac{r_a-r_p}{r_a r_p}\right] \quad\left[\text { As } v_p=\frac{v_a r_a}{r_p}\right]
\end{aligned}
$

Applying the conservation of mechanical energy at perigee and apogee

$
\begin{aligned}
& \frac{1}{2} m v_p^2-\frac{G M m}{r_p}=\frac{1}{2} m v_a^2-\frac{G M m}{r_a} \Rightarrow v_p^2-v_a^2=2 G M\left[\frac{1}{r_p}-\frac{1}{r_a}\right] \\
\Rightarrow & v_a^2\left[\frac{r_a^2-r_p^2}{r_p^2}\right]^2=2 G M\left[\frac{r_a-r_p}{r_a r_p}\right] \quad\left[\text { As } v_p=\frac{v_a r_a}{r_p}\right] \\
\Rightarrow & v_a^2=\frac{2 G M}{r_a+r_p}\left[\frac{r_p}{r_r}\right] \Rightarrow v_a^2=\frac{2 G M}{2 a}\left(\frac{a-c}{a+c}\right)=\frac{G M}{a}\left(\frac{1-e}{1+e}\right)
\end{aligned}
$
Thus the speeds of the planet at apogee and perigee are

$
v_a=\sqrt{\frac{G M}{a}\left(\frac{1-e}{1+e}\right)}, \quad v_p=\sqrt{\frac{G M}{a}\left(\frac{1+e}{1-e}\right)}
$

Recommended Topic Video

Solved Examples Based on Orbital Velocity

Example 1: The ratio of velocities of a planet at perigee and apogee $\frac{v_p}{v_a}$ is equal to

1) 1
2) $\frac{1-e}{1+e}$
3) $\frac{1+e}{1-e}$
4) $\frac{1+e^2}{1-e^2}$

Solution:

The velocity of the planet in terms of Eccentricity

$\begin{aligned} & V_a=\sqrt{\frac{G M}{a}\left(\frac{1-e}{1+e}\right)} \\ & V_p=\sqrt{\frac{G M}{a}\left(\frac{1+e}{1-e}\right)} \\ & V_A=\text { The velocity of the planet at apogee } \\ & V_p=\text { Velocityo fperigee } \\ & \text { wherein } \\ & \text { Eccentricity (e) }=\frac{c}{a} \\ & r_p=a-c \\ & r_a=a+c\end{aligned}$

By conservation of angular momentum,

$\begin{aligned} & m v_p r_p=m v_a r_a \\ & \Rightarrow \frac{v_p}{v_a}=\frac{r_a}{r_p}=\frac{a+c}{a-c}=\frac{1+e}{1-e}\end{aligned}$

Hence, the answer is the option (3).

Example 2: A satellite is in an all-optical orbit around planet P. It is observed that the velocity of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet. The ratio of distances b/w the satellite and the planet at closest and farthest point is

1)

2)

3)

4)

Solution:

As the angular momentum remains conserved. So,
$
\begin{aligned}
& L_{\text {Nearest }}=L_{\text {Farthest }} \\
& m \times v_n \times r_n=m \times v_f \times r_f
\end{aligned}
$
Also,

$
V_f=\frac{V_n}{6}
$
As,

$
\begin{aligned}
& V_n \times r_n=V_f \times r_f \\
& V_n \times r_n=\frac{V_n}{6} \times r_f
\end{aligned}
$
So,

$
\frac{r_n}{r_f}=\frac{1}{6}
$

Hence, the answer is the option (2).

Summary

Orbital velocity is the speed required for an object to maintain a stable orbit around a celestial body, balancing gravitational pull with forward motion. It is determined using the formula v = $\sqrt{\frac{G M}{r}}$. where G is the gravitational constant, M is the mass of the celestial body, and r is the distance from its centre. For elliptical orbits, the velocities at apogee (farthest point) and perigee (closest point) are given by $V_a=\sqrt{\frac{G M}{a}\left(\frac{1-e}{1+e}\right)}$ and $V_p=\sqrt{\frac{G M}{a}\left(\frac{1+e}{1-e}\right)}$ respectively. Examples illustrate how these velocities relate to orbital parameters and conservation laws.