Parallel Perpendicular Axes Theorem - Statement, Formula, FAQs

Edited By Vishal kumar | Updated on Jul 02, 2025 05:02 PM IST

Theorems on parallel and perpendicular axes are basic theorems used in rotational mechanics to simplify the calculation of moment of inertia. The Theorem of Parallel Axes states how the moment of inertia of the body about an axis can be derived from its moment of inertia about a parallel axis on the other hand, the perpendicular theorem states that the moment of inertia of a body about an axis perpendicular to its plane is equal to the sum of its moments about any two mutually perpendicular axes in its plane which intersect each other at the point where the perpendicular axis pass through it.

This Story also Contains

What is a Moment of Inertia?
What is the Parallel Axis Theorem?
Parallel Axis Theorem Formula
Parallel Axis Theorem Derivation
Perpendicular Axis Theorem
Perpendicular Axis Theorem Formula

Parallel Perpendicular Axes Theorem - Statement, Formula, FAQs

What is a Moment of Inertia?

We know that inertia is a property that a body already has, to resist the change in its linear state of motion or state of rest. This is a property that measures the mass of the body. However, the moment of inertia which is denoted by (I) is the measure of property or ability of a body to resist its state of rotational motion. It plays the same exact role in rotational motion as mass plays in linear motion and hence we can draw an analogy between them.

So, we can define the moment of inertia as the property of a body to oppose any change in its state of uniform motion or its state of rest $\mathrm{I}=\mathrm{Mr}^2$, where r is the perpendicular distance of a particle from the rotational axis and M is the mass of the body in rotational motion.

Also, read

What is the Parallel Axis Theorem?

The moment of inertia of a body about an axis that passes through its centre is equal to the sum of that about an axis which passes through its centre, and the product of the mass of the body and the square of the distance between the two axes.

Parallel Axis Theorem Formula

The parallel axis theorem statement can be expressed as follows:

$$
\mathrm{I}=\mathrm{I}_{\mathrm{C}}+\mathrm{Mh}^2
$$
Where,
I is the moment of inertia of the body
$\mathrm{I}_{\mathrm{C}}$ is the moment of inertia about the center
$M$ is the mass of the body
$\mathrm{h}^2$ is the square of the distance between the two axes

Parallel Axis Theorem Derivation

Let $\mathrm{I}_{\mathrm{C}}$ be the moment of inertia of an axis that is passing through the centre of mass (AB from the figure) and I will be the moment of inertia about the axis $A^{\prime} B^{\prime}$ at a distance of $h$.

Consider a particle of mass $m$ at a distance $r$ from the centre of gravity of the body. Then,
Distance from $A^{\prime} B^{\prime}=r+h$

$$
\begin{aligned}
& I=\sum m(r+h)^2 \\
& I=\sum m\left(r^2+h^2+2 r h\right) \\
& I=\sum m r^2+\sum m h^2+\sum 2 r h \\
& I=I_C+h 2 \sum m+2 h \sum m r \\
& I=I_C+M h^2+0 \\
& I=I_C+M h^2
\end{aligned}
$$

Related Topics

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Perpendicular Axis Theorem

The perpendicular axis theorem states that for any plane body, the moment of inertia about any of its axes which are perpendicular to the plane is equal to the sum of the moment of inertia about any two perpendicular axes in the plane of the body which intersect the first axis in the plane.

Perpendicular Axis Theorem Formula

The perpendicular axis theorem is used when the body is symmetric in shape about two out of the three axes. If the moment of inertia about two of the axes is known the moment of inertia about the third axis can be found using the expression:

perpendicular axis theorem

$$
I_a=I_b+I_c
$$

Frequently Asked Questions (FAQs)

1. Find out the relation between I1 and I2, where I1 and I2 are moments of inertia of a rigid body of mass m as in fig-6.

We use the parallel axis theorem- I1 =Icom+ma2 and I2=Icom+mb2

Therefore, I1 - I2=m(a2-b2)

2. Find the moment of inertia of a disc about an axis through its tangent and perpendicular to the plane. (See figure-7)

First we will find moment of inertia about an axis passing through its center and

perpendicular to the plane i.e. Icom

For this, consider an elementary ring of mass dm and width dr at a distance r from the center of

disc. Then, moment of inertia for the elementary ring is- dI=dm.r2

As, dm=MR2.2πrdr

Then, Icom =dIring=0RMR2.2πrdr.r2=MR2/2

Now, to find moment of inertia about axis through its tangent, we use parallel axis theorem-

I=Icom+ MR2, as h=R here.

I=3MR22

3. Find the moment of inertia of a given sphere (uniform) having a mass m and radius R about any tangent if the sphere is a solid.

We use parallel axis theorem, I=ICOM+Mh2

ICOM=25mR2 , d=R here

Therefore, I=75mR2

4. Find moment of inertia of a disc about an axis parallel to its plane and passing through its center of mass (see figure-8).

We already know that, Icom= MR2/2

By perpendicular axis theorem formula, Iz=Ix+Iy

=> MR2/2= 2ID, as the ring is symmetrical, thus Ix=Iy=ID

=>ID=(14)MR2

5. 5. We are given a symmetric lamina of mass M consisting of a square shape with a semicircular section over each edge of the square as in figure-9. The side of the square is given 2a.The moment of inertia of the lamina about an axis through its center of m

Using perpendicular axis theorem-

Ix=Iy

2Ix= 1.6 Ma2

Ix=0.8Ma2

IAB=Ix+M(2a)2=4.8Ma2

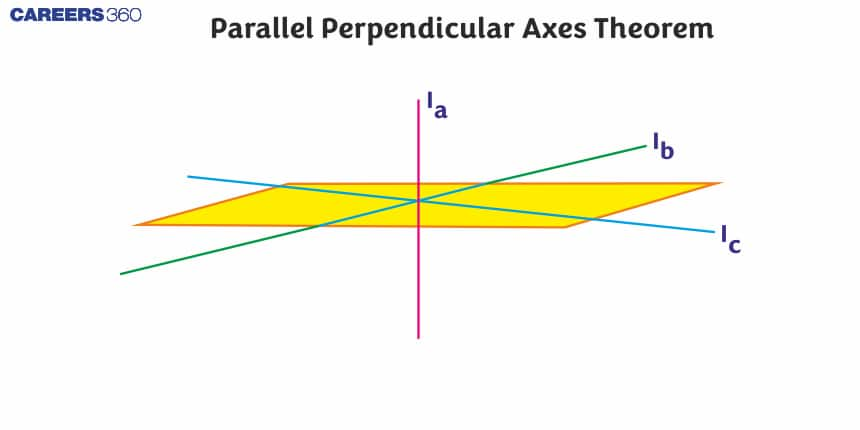
6. What is the formula for the perpendicular axis theorem?

Iz=Ix+Iy , where I’s are the moments of inertia in Z, X and Y axes respectively.

7. What is the formula for the parallel axis theorem?

I=ICOM+Mh2, h is the perpendicular distance between the axis passing through the COM and the axis about which we have to find the moment of inertia. Both of these axes of rotation must be parallel to each other.

8. What happens to the moment of inertia if the axis of rotation passes through the center of mass?

If the axis of rotation passes through the center of mass, the distance d in the Parallel Axes Theorem becomes zero. Therefore, the moment of inertia about this axis is simply I_cm, the moment of inertia about the center of mass.

9. How does the Parallel Axes Theorem affect the moment of inertia as the axis moves away from the center of mass?

As the axis moves farther from the center of mass, the moment of inertia increases. This is because the Md^2 term in the formula becomes larger as the distance d increases, resulting in a greater moment of inertia.

10. How does mass distribution affect the application of these theorems?

Mass distribution is crucial in applying these theorems. For the Parallel Axes Theorem, a more spread-out mass distribution will result in a larger increase in moment of inertia as the axis moves away from the center of mass. For the Perpendicular Axes Theorem, the mass distribution determines the relative magnitudes of the moments of inertia about different axes.

11. Can the Parallel Axes Theorem be applied in reverse to find the center of mass?

While the theorem itself doesn't directly give the center of mass, it can be used in conjunction with experimental measurements to locate the center of mass. By measuring the moment of inertia about multiple parallel axes, one can determine the axis that passes through the center of mass.

12. How do these theorems simplify calculations in physics problems?

These theorems simplify calculations by allowing us to relate moments of inertia about different axes. Instead of calculating the moment of inertia from scratch for each new axis, we can use known values and these theorems to quickly determine new moments of inertia.

13. What is the Perpendicular Axes Theorem?

The Perpendicular Axes Theorem states that for a planar object, the moment of inertia about an axis perpendicular to the plane is equal to the sum of the moments of inertia about any two perpendicular axes in the plane that intersect at the point where the perpendicular axis passes through the plane.

14. How is the Perpendicular Axes Theorem expressed mathematically?

The Perpendicular Axes Theorem is expressed as: I_z = I_x + I_y, where I_z is the moment of inertia about the axis perpendicular to the plane, and I_x and I_y are the moments of inertia about two perpendicular axes in the plane.

15. Why are these theorems important in rotational motion?

These theorems are important because they allow us to calculate the moment of inertia of an object about any axis, given its moment of inertia about a known axis. This simplifies calculations in many rotational motion problems and helps in understanding the distribution of mass in objects.

16. What is the main difference between the Parallel and Perpendicular Axes Theorems?

The main difference is that the Parallel Axes Theorem relates the moments of inertia about parallel axes, while the Perpendicular Axes Theorem relates the moments of inertia about perpendicular axes in a planar object.

17. Why is the Perpendicular Axes Theorem limited to planar objects?

The Perpendicular Axes Theorem is limited to planar objects because it relies on the geometry of two-dimensional shapes. For three-dimensional objects, the distribution of mass in the third dimension affects the moment of inertia in ways not accounted for by this theorem.

18. What is the Parallel Axes Theorem?

The Parallel Axes Theorem states that the moment of inertia of an object about any axis parallel to an axis passing through its center of mass is equal to the moment of inertia about the center of mass axis plus the product of the object's mass and the square of the perpendicular distance between the two axes.

19. How is the Parallel Axes Theorem expressed mathematically?

The Parallel Axes Theorem is expressed as: I = I_cm + Md^2, where I is the moment of inertia about the new axis, I_cm is the moment of inertia about the center of mass axis, M is the mass of the object, and d is the perpendicular distance between the two axes.

20. Can the Parallel Axes Theorem be applied to any shape?

Yes, the Parallel Axes Theorem can be applied to any rigid body, regardless of its shape. It works for both regular and irregular objects, as long as we know the object's mass and the distance between the axes.

21. Can the Parallel Axes Theorem be used to find the moment of inertia about the center of mass?

Yes, if we know the moment of inertia about any parallel axis and the distance between that axis and the center of mass, we can rearrange the formula to solve for I_cm: I_cm = I - Md^2.

22. How does the Parallel Axes Theorem relate to the concept of rotational kinetic energy?

The Parallel Axes Theorem directly affects rotational kinetic energy calculations. Since rotational kinetic energy is given by (1/2)Iω^2, where I is the moment of inertia and ω is the angular velocity, changing the axis of rotation will change the moment of inertia and thus the rotational kinetic energy.

23. How do these theorems relate to the concept of rotational inertia?

These theorems directly deal with rotational inertia, which is another term for moment of inertia. They provide methods to calculate and relate rotational inertia about different axes, helping us understand how objects resist changes to their rotational motion.

24. What role do these theorems play in the study of precession and nutation?

While these theorems don't directly describe precession and nutation, they are fundamental in calculating the moments of inertia necessary to analyze these complex rotational motions. The Perpendicular Axes Theorem is particularly relevant in understanding the different moments of inertia that contribute to these phenomena.

25. How does the application of these theorems differ for solid objects versus hollow objects?

The theorems apply equally to solid and hollow objects, but the results can be quite different. Hollow objects often have a larger moment of inertia about their center of mass compared to solid objects of the same mass and outer dimensions. This difference becomes more pronounced when using the Parallel Axes Theorem to calculate moments of inertia about non-central axes.

26. How do these theorems apply to objects with non-uniform density?

These theorems apply equally to objects with non-uniform density. The non-uniform density is accounted for in the calculation of the moment of inertia about the center of mass (I_cm). Once I_cm is known, the theorems can be applied regardless of the object's internal mass distribution.

27. Can the Parallel Axes Theorem be used to minimize the moment of inertia of a rotating object?

Yes, the Parallel Axes Theorem shows that the moment of inertia is minimized when the axis of rotation passes through the center of mass. This principle is used in designing efficient rotating machinery, where minimizing moment of inertia can reduce energy requirements.

28. Can the Perpendicular Axes Theorem be used for any set of perpendicular axes in a plane?

Yes, as long as the object is planar and the axes are perpendicular to each other and lie in the plane of the object, the theorem can be applied regardless of the specific orientation of the axes within that plane.

29. How does the Perpendicular Axes Theorem help in understanding the behavior of flat rotating objects?

The Perpendicular Axes Theorem helps us understand how the resistance to rotation of a flat object relates to its shape and mass distribution in different directions. It shows that the resistance to rotation about an axis perpendicular to the plane is the sum of the resistances about two perpendicular axes in the plane.

30. What is the significance of the Md^2 term in the Parallel Axes Theorem?

The Md^2 term represents the additional moment of inertia due to the object's mass being offset from the axis of rotation. It accounts for the fact that mass farther from the axis of rotation contributes more to the moment of inertia, following the principle that I = mr^2.

31. How do these theorems relate to the concept of radius of gyration?

The radius of gyration, k, is defined by the equation I = Mk^2. The Parallel Axes Theorem can be expressed in terms of radii of gyration as k^2 = k_cm^2 + d^2, where k_cm is the radius of gyration about the center of mass.

32. Can the Parallel Axes Theorem be used for rotating systems with multiple objects?

Yes, the Parallel Axes Theorem can be applied to systems of multiple objects. The total moment of inertia of the system about any axis is the sum of the moments of inertia of each object about that axis, which can be calculated using the theorem for each object individually.

33. How does the Perpendicular Axes Theorem apply to symmetrical objects?

For symmetrical objects, the Perpendicular Axes Theorem can simplify calculations. For example, in a square or circular plate, the moments of inertia about any two perpendicular axes in the plane are equal due to symmetry, so I_z = 2I_x = 2I_y.

34. What is the relationship between these theorems and conservation of angular momentum?

While these theorems don't directly involve angular momentum, they are crucial in calculating moments of inertia, which are essential in applying conservation of angular momentum. Changes in moment of inertia due to shifts in axis location (as described by these theorems) can lead to changes in angular velocity to conserve angular momentum.

35. How do these theorems apply to real-world rotating objects like wheels or turbines?

These theorems are widely used in engineering to analyze rotating machinery. For instance, the Parallel Axes Theorem is used to calculate the moment of inertia of a wheel about its axle, given its moment of inertia about its center. This is crucial in designing vehicles, turbines, and other rotating systems.

36. Can the Parallel Axes Theorem be applied to objects rotating about an axis that isn't parallel to the center of mass axis?

No, the Parallel Axes Theorem only applies to axes that are parallel to each other. For non-parallel axes, more complex calculations involving the inertia tensor are required.

37. Can these theorems be applied to objects in non-inertial reference frames?

Yes, these theorems can be applied in non-inertial reference frames. However, when dealing with rotating reference frames, additional terms like the Coriolis effect may need to be considered in the overall analysis of the object's motion.

38. How do these theorems relate to the parallel-axis and perpendicular-axis shifts in the inertia tensor?

These theorems are essentially scalar versions of more general tensor transformations. The Parallel Axes Theorem corresponds to a parallel-axis shift of the inertia tensor, while the Perpendicular Axes Theorem relates to specific components of the inertia tensor for planar objects.

39. What is the historical significance of these theorems in the development of classical mechanics?

These theorems, developed in the 18th century, were crucial in advancing the understanding of rotational dynamics. They allowed physicists to solve complex rotational problems and laid the groundwork for more advanced concepts in classical mechanics and later in quantum mechanics.

40. How does the concept of parallel axes relate to the stability of rotating objects?

The Parallel Axes Theorem helps explain why objects are more stable when rotating about an axis through their center of mass. As the axis moves away from the center of mass, the moment of inertia increases, requiring more energy to change the rotational motion and thus increasing stability.

41. What are some common misconceptions about the application of these theorems?

Common misconceptions include thinking that the Parallel Axes Theorem applies to any two axes (not just parallel ones), assuming the Perpendicular Axes Theorem works for all 3D objects, and believing that these theorems directly give the center of mass location.

42. How do these theorems relate to the concept of angular momentum in quantum mechanics?

While these theorems are classical mechanics concepts, they have analogues in quantum mechanics. The idea of moment of inertia and its transformation between different axes is related to the angular momentum operators and their properties in quantum systems.

43. Can the Perpendicular Axes Theorem be extended to non-planar objects in any way?

The Perpendicular Axes Theorem as stated only applies to planar objects. For non-planar objects, more general approaches using the full inertia tensor are necessary. However, the principle behind the theorem can sometimes be applied to specific symmetrical 3D objects on a case-by-case basis.

44. How do these theorems apply to objects that are changing shape, like a gymnast during a routine?

For objects changing shape, these theorems can be applied instantaneously at any given moment. However, as the shape changes, the moment of inertia about the center of mass (I_cm) will change, affecting the calculations. This is why gymnasts can control their rotation speed by changing their body configuration.

45. What is the relationship between these theorems and the concept of principal axes of inertia?

Principal axes of inertia are axes about which the moment of inertia is either a maximum or minimum. While these theorems don't directly determine principal axes, they are often used in conjunction with the concept. The Perpendicular Axes Theorem, in particular, can simplify the process of finding principal axes for planar objects.

46. How do these theorems help in understanding the motion of celestial bodies?

These theorems are crucial in analyzing the rotational behavior of planets, moons, and asteroids. They help in calculating the moments of inertia of these bodies, which is essential for understanding phenomena like precession, tidal locking, and the stability of rotation axes.

47. Can these theorems be applied to fluid dynamics problems?

While these theorems were developed for rigid bodies, they can be applied to fluids in certain cases, particularly for analyzing the rotation of fluid bodies as a whole. However, for detailed fluid dynamics, more complex methods accounting for fluid deformation are usually necessary.

48. How do these theorems relate to the concept of torque?

These theorems don't directly involve torque, but they are crucial in relating torque to rotational motion. The moment of inertia, which these theorems help calculate, determines how an object responds to applied torques through the equation τ = Iα, where τ is torque, I is moment of inertia, and α is angular acceleration.

49. What role do these theorems play in the design of gyroscopes and inertial guidance systems?

These theorems are fundamental in designing gyroscopes and inertial guidance systems. They help engineers calculate and optimize the moments of inertia of rotating components, which is crucial for the precision and stability of these devices.

50. How do these theorems apply to objects with complex geometries?

For objects with complex geometries, these theorems are often applied in combination with integral calculus or numerical methods. The object can be divided into simpler shapes, the moment of inertia calculated for each part, and then the theorems used to combine these into the total moment of inertia.

51. Can the Parallel Axes Theorem be used to analyze the energy of a compound pendulum?

Yes, the Parallel Axes Theorem is crucial in analyzing compound pendulums. It allows the calculation of the moment of inertia about the pivot point, given the moment of inertia about the center of mass, which is essential for determining the pendulum's period and energy.

52. How do these theorems relate to the concept of rotational equilibrium?

While these theorems don't directly determine rotational equilibrium, they are essential in calculating the moments of inertia needed to analyze equilibrium conditions. Understanding how moment of inertia changes with axis position helps in analyzing stability and balance in rotational systems.

53. What is the significance of these theorems in the context of angular momentum conservation?

These theorems help explain how changes in an object's configuration can affect its rotation while conserving angular momentum. For instance, the Parallel Axes Theorem shows why bringing mass closer to the rotation axis (reducing d) decreases the moment of inertia, causing an increase in angular velocity to conserve angular momentum.

54. How do these theorems apply to systems with changing mass, like rockets?

For systems with changing mass, these theorems can be applied at any instant, but the calculations must be updated as the mass changes. In the case of rockets, the changing mass and mass distribution affect the moment of inertia, which these theorems help calculate throughout the rocket's flight.

55. Can these theorems be used in analyzing the motion of articulated bodies, like robotic arms?

Yes, these theorems are valuable in robotics for analyzing articulated bodies. They help in calculating the moments of inertia of individual segments and how they contribute to the overall rotational dynamics of the