Potential Energy Of A Dipole In An Electric Field

The potential energy of a dipole in an electric field is a concept that bridges fundamental physics with real-life applications. Imagine holding a bar magnet near a fridge; the magnet aligns itself due to the fridge’s magnetic field, minimizing its potential energy. Similarly, a dipole—consisting of two equal and opposite charges separated by a distance—experiences forces in an electric field, leading to a change in its orientation and potential energy. This concept is crucial in understanding molecular behaviour, designing electronic devices, and even in medical imaging techniques like MRI, where dipoles in atoms interact with external fields. In this article, we will understand the Potential energy of a dipole in an electric field. it helps explain how systems tend to move towards states of lower energy, a principle observed in many natural and engineered processes.

This Story also Contains

1. Potential Energy of a Dipole in an Electric Field
2. Equilibrium of Dipole
3. Solved Examples Based on Potential Energy of a Dipole In an Electric Field
4. Summary

Potential Energy of a Dipole in an Electric Field

The potential energy of a dipole in an electric field is a fundamental concept in electromagnetism that has wide-ranging implications in both natural phenomena and technological applications. A dipole, which consists of two opposite charges separated by a distance, interacts with an external electric field in a way that causes it to align with the field. This alignment results in a change in the dipole's potential energy, depending on the angle between the dipole moment and the electric field.

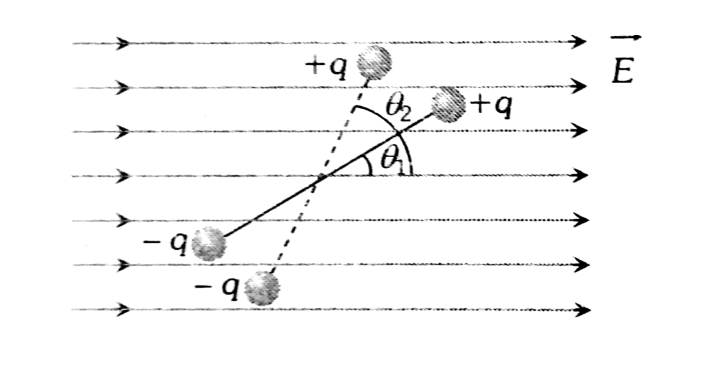
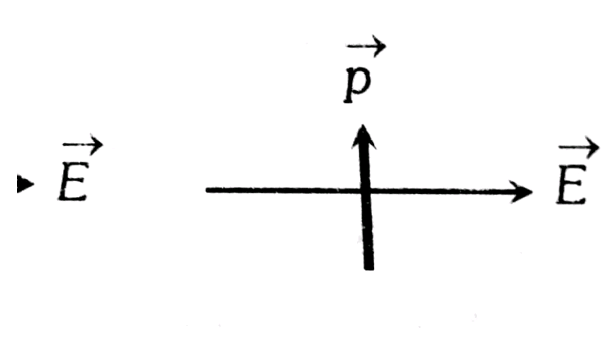
When a dipole is kept in a uniform electric field. The net force experienced by the dipole is zero as shown in the below figure.

I.e $F_{net}=0$

But it will experience torque. The net torque about the centre of the dipole is given as

$\tau =QEd\sin \theta$ or $\tau =PE\sin \theta$ or $\overrightarrow{\tau }=\overrightarrow{P}\times \overrightarrow{E}$

Work Done in Rotation

The concept of work done in rotation is central to understanding how energy is transferred in rotational systems, much like how work is done in linear motion. When a force is applied to an object, causing it to rotate around an axis, work is done to change the object's rotational state. This is similar to pushing a door to open it, where the force applied at the handle causes the door to rotate about its hinges. The amount of work done depends on the magnitude of the force, the distance from the axis of rotation (which is the lever arm), and the angle at which the force is applied.

Then work done by electric force for rotating a dipole through an angle ${\theta }_2$ from the equilibrium position of an angle ${\theta }_1$ (As shown in the above figure) is given as

$\begin{array}{rl}& W_{\text{ele}}=\int \tau d\theta ={\int }_{{\theta }_1}^{{\theta }_2}\tau d\theta \cos \left({180}^0\right)=-{\int }_{{\theta }_1}^{{\theta }_2}\tau d\theta \\ & \Rightarrow W_{\text{ele}}=-{\int }_{{\theta }_1}^{{\theta }_2}(P\times E)d\theta =-{\int }_{{\theta }_1}^{{\theta }_2}(PE\mathrm{Sin}\theta )d\theta =PE(\cos {\theta }_2-\cos {\theta }_1)\end{array}$

And So work done by an external force is $W=PE(\cos {\mathrm{\Theta }}_1-\cos {\mathrm{\Theta }}_2)$

For example

$\begin{array}{rl}& \text{if}{\theta }_1=0^{\circ }\text{and}{\theta }_2=\theta \\ & W=PE(1-\cos \theta )\\ & \text{if}{\theta }_1={90}^{\circ }\text{and}{\theta }_2=\mathrm{\Theta }\\ & W=-PE\cos \theta \end{array}$

Potential Energy of a Dipole Kept in an Electric Field

The potential energy of a dipole in an electric field is a crucial concept that describes how a dipole interacts with an external electric field. A dipole consists of two equal and opposite charges separated by a distance, creating a dipole moment. When this dipole is placed in an electric field, it experiences a torque that tends to align it with the direction of the field.

As $\mathrm{\Delta }U=-W_{\text{ele}}=W$

So change in the Potential Energy of a dipole when it is rotated through an angle ${\theta }_2$ from the equilibrium position of an angle ${\theta }_1$ is given as $\mathrm{\Delta }U=PE(\cos {\theta }_1-\cos {\theta }_2)$

$\begin{array}{rl}& \text{if}{\theta }_1={90}^{\circ }\text{and}{\theta }_2=\theta \\ & \mathrm{\Delta }U=U_{{\theta }_2}-U_{{\theta }_1}=U_{\theta }-U_{90}=-PE\cos \theta \end{array}$

Assuming ${\theta }_1={90}^{\circ }$ and $U_{{90}^{\circ }}=0$
we can write $U=U_{\theta }=-\overrightarrow{P}\cdot \overrightarrow{E}$

Equilibrium of Dipole

The equilibrium of a dipole in an electric field is a condition where the dipole experiences no net torque, resulting in a stable or unstable configuration. A dipole consists of two equal and opposite charges separated by a distance, creating a dipole moment. When placed in an external electric field, the dipole experiences forces that tend to rotate it, aligning the dipole moment with the field.

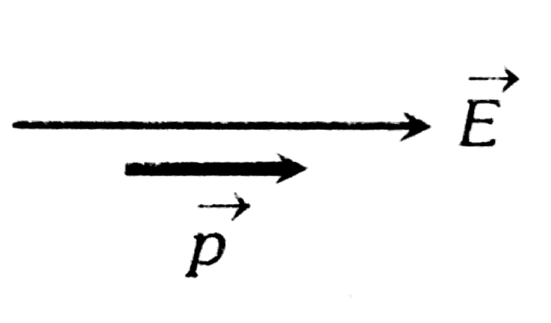
1. Stable Equilibrium

This occurs when the dipole is aligned with the electric field, meaning the dipole moment $\overrightarrow{p}$ is parallel to the field $\overrightarrow{E}$. In this position, the potential energy is minimized, and any small disturbance will result in a restoring torque that brings the dipole back to this position. It’s similar to a pendulum hanging straight down—it will return to the lowest point when disturbed.

$\begin{array}{rl}& \theta =0^{\circ }\\ & \tau =0\\ & U_{min}=-PE\end{array}$

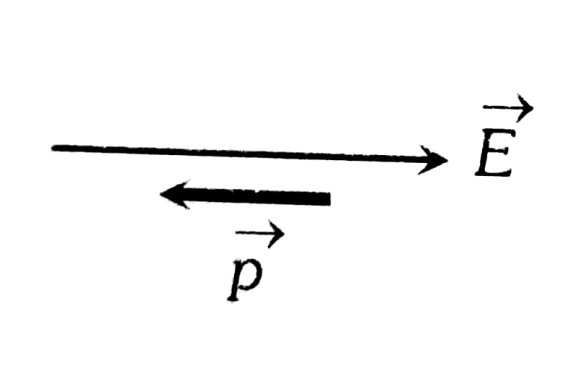
2. Unstable Equilibrium

This occurs when the dipole is aligned opposite to the electric field, meaning the dipole moment $\overrightarrow{p}$ is anti-parallel to the field $\overrightarrow{E}$. In this position, the potential energy is maximized, and any small disturbance will cause the dipole to rotate away from this alignment, rather than returning to it. It’s like trying to balance a pencil on its tip—any small push will cause it to fall over.

$\begin{array}{rl}& \theta ={180}^{\circ }\\ & \tau =0\\ & U_{\text{max}}=PE\end{array}$

Note

When $\theta ={90}^{\circ }$
then ${\tau }_{max}=PE$ and $U=0$

and it is important to note here that the dipole is not in equilibrium since ${\tau }_{max}\ne 0$

Recommended Topic Video

Solved Examples Based on Potential Energy of a Dipole In an Electric Field

Example 1: An electric dipole of moment $\overrightarrow{p}$ placed in a uniform electric field $\overrightarrow{E}$ has minimum potential energy when the angle between $\overrightarrow{p}$ and $\overrightarrow{E}$ is

1) zero
2) $\pi /2$
3) $\pi$
4) $3\pi /2$

Solution:

Work done in rotation

$\begin{array}{rl}& \text{if}{\theta }_1={90}^{\circ }\text{and}{\theta }_2=\theta \\ & W=U=-PE\cos \theta \\ & U=-\overrightarrow{P}\cdot \overrightarrow{E}\\ & U=-pE\cos \theta \text{It has a minimum value when}\theta =0^{\circ }\\ & \text{i.e.}{U}_m\text{in}=-pE\times \cos 0^{\circ }=-pE\end{array}$

Hence, the answer is the option (1).

Example 2: An electric field of 1000 V/m is applied to an electric dipole at an angle of 45^o. The value of the electric dipole moment is 10^-29 C.m. What is the potential energy of the electric dipole?

1)- 20 x 10^-18 J

2)- 10 x 10^-29 J

3) - 7 x 10^-27 J

4)- 9 x 10^-20 J

Solution:

$\begin{array}{rl}& U=-\overrightarrow{p}\cdot \overrightarrow{E}\\ & p={10}^{-29}\\ & \overrightarrow{E}=1000\mathrm{v}/\mathrm{m}\\ & \theta =45\\ & U=-pE\cos \theta \\ & =-({10}^{-29}\times {10}^3\times \frac{1}{\sqrt{2}})\\ & U=-7\times {10}^{-27}J\end{array}$

Hence, the answer is the option (3).

Example 3: Two charges $+3.2\times {10}^{-19}$ and $-3.2\times {10}^{-19}$ kept 2.4 Å apart form a dipole. If it is kept in the uniform electric field of intensity $4\times {10}^5\mathrm{volt}/\mathrm{m}$ then what will be its electrical energy in equilibrium

1) $+3\times {10}^{-23}\mathrm{J}$
2) $-3\times {10}^{-23}\mathrm{J}$
3) $-6\times {10}^{-23}J$
4) $-2\times {10}^{-23}J$

Solution:

Stable Equilibrium

$\begin{array}{rl}& \theta ={90}^{\circ }\\ & \tau =0\\ & w=0\\ & U_{min}=-PE\end{array}$

wherein

The potential energy of the electric dipole

$\begin{array}{rl}& U=-pE\cos \theta =-(q\times 2l)E\cos \theta \\ & U=-(3.2\ast {10}^{-19}\ast 2.4\ast {10}^{-10})4\ast {10}^5\cos \theta \\ & U=-(3\ast {10}^{-23})\text{(approx.)}\end{array}$

Hence, the answer is the option (2).

Example 4: Electric charges $q,q,-2q$ are placed at the corners of an equilateral triangle ABC of side l. The magnitude of the electric dipole moment of the system is

1) ql
2) 2 ql
3) $\sqrt{3}ql$
4) 4 ql

Solution:

$P_{net}=\sqrt{P^2+P^2+2PP\cos {60}^{\circ }}=\sqrt{3}p=\sqrt{3}ql(\because p=ql)$

Hence, the answer is the option (1).

Example 5: When an electric dipole $\overrightarrow{p}$ is placed in a uniform electric field $\overrightarrow{E}$ then at what angle between $\overrightarrow{p}$ and $\overrightarrow{E}$ the value of torque will be the maximum

1) ${90}^{\circ }$
2) $0^{\circ }$
3) ${180}^{\circ }$
4) ${45}^{\circ }$

Solution:

Not in equilibrium

$\begin{array}{rl}& \theta ={90}^{\circ }\\ & {\tau }_{max}=PE\\ & w=PE\\ & U=0\end{array}$

wherein

Maximum torque $=pE$ so the angle should be 90.

Summary

The potential energy of a dipole in an electric field is a key concept in understanding how dipoles align with external fields, resulting in changes in their potential energy. This interaction leads to either stable or unstable equilibrium, depending on the dipole's orientation. The work done in rotating a dipole within an electric field further illustrates how systems move toward states of lower energy, a principle observed in both natural and engineered processes.