Power And Power Factor In AC Circuits

Power and power factors are critical concepts in alternating current (AC) circuits, essential for understanding how electrical energy is utilized efficiently. Power in AC circuits can be classified into active power, reactive power, and apparent power, each representing different aspects of energy consumption and transfer. The power factor, a measure of how effectively electrical power is converted into useful work, is crucial in minimizing energy losses and optimizing the performance of electrical systems. In real life, improving the power factor in industrial and residential settings reduces electricity bills and enhances the longevity of electrical equipment. This article explores the intricacies of power and power factors in AC circuits and their significance in practical applications.

This Story also Contains

1. Power in an AC Circuit
2. Solved Examples Based on Power in an AC Circuit
3. Example 1: Calculate power (in watts) when the rms value of voltage and current are 220v & 3A respectively. The phase between the voltage of the current is π4
4. Summary

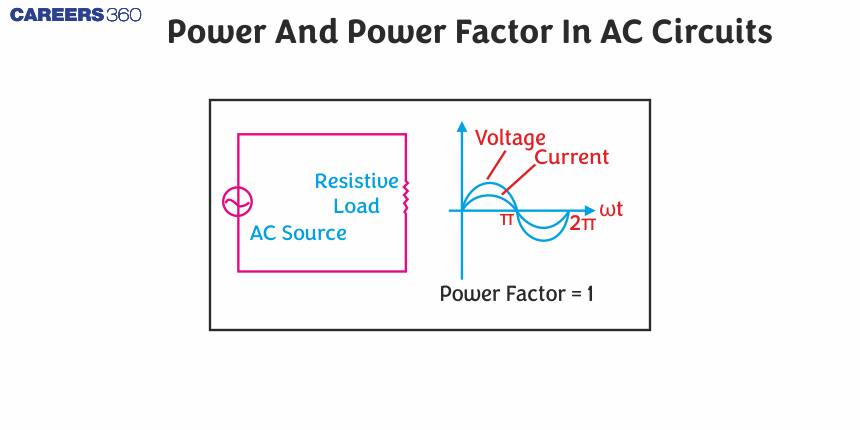
Power in an AC Circuit

Power in an AC circuit refers to the rate at which electrical energy is transferred by an electric circuit. In alternating current (AC) circuits, power is not as straightforward as in direct current (DC) circuits due to the oscillating nature of voltage and current. we can say that the voltage v = v_m sinωt applied to a series RLC circuit drives a current in the circuit given by i = i_m sin(ωt + φ) where,

$i_m=\frac{v_m}{Z}$ and $\varphi ={\tan }^{-1}\left(\frac{X_C-X_L}{R}\right)$

So, the instantaneous power is equal to

$$P_{\text{instantaneous}}=vi=(v_m\sin \omega t)\times [i_m\sin (\omega t+\varphi )]$$

By applying trigonometric application we get,
$$P_{\text{instaneous}}=\frac{v_{m}i}{2}[\cos \varphi -\cos (2\omega t+\varphi )]$$

If we calculate the average power, then the second term of RHS will become zero. Because it is time-dependent and during one complete cycle, the summation will become zero.

$\begin{array}{rl}{P}_{\text{Average}}& =\frac{v_m{i}_m}{2}\cos \varphi =\frac{v_m}{\sqrt{2}}\frac{i_m}{\sqrt{2}}\cos \varphi \\ P_{\text{Average}}& =VI\cos \varphi \\ P_{\text{Average}}& =I^{2}Z\cos \varphi \end{array}$

From the above equation we can see that the average power dissipated depends on the voltage and current and the cosine of the phase angle φ between them. The quantity cosφ is called the power factor.

Let us discuss the power factor for various cases

• Resistive circuit: If in the circuit, only pure R is present, it is called resistive.circuit In that case φ = 0, because cos φ =1. And if the power factor is 1, then there is maximum power dissipation.
• Purely inductive or capacitive circuit: From the previous concept and from the phasor diagram of these cases, we can say that, if the circuit contains only an inductor or capacitor then the phase difference between voltage and current is $\frac{\pi }{2}$. Therefore, cos φ = 0, and no power is dissipated even though a current is flowing in the circuit. This current is referred to as a wattless current.
• LCR series circuit: As we know the phase angle in this case is

$\phi ={\tan }^{-1}\frac{X_L-X_C}{R}$

So, maybe non-zero in R-L, R-C or R-L-C. And if it is non-zero, then there must be some power dissipation but that power dissipation is only in resistor.

• The power dissipated at resonance in the LCR circuit: As we know at resonance,$X_C-X_L=0$ , So, phase angle (φ) = 0. Therefore, cosφ = 1. So, $P=I^{2}Z=I^{2}R$. That is, maximum power is dissipated in a circuit at resonance. The total dissipation is through a resistor.

Apparent or Virtual Power

Apparent or virtual power in an AC circuit is the product of the root mean square (RMS) values of voltage and current. It represents the total power flowing through the circuit, combining both active (real) and reactive power. The product of apparent voltage and apparent current in an electrical circuit. Apparent power be always positive

$P_{app}=V_{rms}{i}_{rms}^{\prime }=\frac{v_0{i}_0^{\prime }}{2}$

Recommended Topic Video

Solved Examples Based on Power in an AC Circuit

Example 1: Calculate power (in watts) when the rms value of voltage and current are 220v & 3A respectively. The phase between the voltage of the current is $\frac{\pi }{4}$

1)466.76

2)660

3)330

4)233.38

Solution:

Average power (True power)

$\begin{array}{rl}& P_{av}=V_{rms}{i}_{rms}\cos \varphi \\ & P=V_{rms}{I}_{rms}\cos \varphi \\ & =220\times 3\times \cos \frac{\pi }{4}=466.76\mathrm{W}\end{array}$

Hence, the answer is the option (1).

Example 2: Find the average power generated (in watts) in the given circuit

1) 39.60

2)40.23

3)36.21

4)35.10

Solution:

Average power

$\begin{array}{rl}& P_{av}=i_{rms}^{\prime 2}R=\frac{V_{rms}^{2}R}{Z^2}\\ & P_{\text{average}}=I_{rms}^2\cdot R=\frac{{\left(V_{rms}\right)}^{2}R}{Z^2}\\ & R=0.2\mathrm{\Omega }\\ & X_L=\omega L=(2\pi f)L=2\pi \times 40\times 40\times 4\times {10}^{-3}=1\mathrm{\Omega }\\ & V_{rms}=\frac{V_o}{\sqrt{2}}=\frac{200}{\sqrt{2}}{P}_{av}={\left(\frac{200}{2}\right)}^2\times \frac{0.2}{{\left(\sqrt{1^2+(0.2{)}^2}\right)}^2}=2\times {10}^{-4}\times \frac{0.2}{1.04}=39.6\mathrm{W}\end{array}$

Hence, the answer is the option (1).

Example 3: Calculate the power factor in a given circuit

1) 1

2) 2

3) 4

4) 0

Solution:

The power factor in resistive circuits

$$\cos \varphi =1$$

Power factor
$$\cos \varphi =\frac{R}{Z}$$
$$\begin{array}{rl}& R=2k\mathrm{\Omega }\\ & Z=\sqrt{R^2+{(X_L-X_C)}^2}=R(X_L=X_C=0)\\ & \therefore \cos \varphi =1\\ & \text{Power factor}=1\end{array}$$

Hence, the answer is the option (1).

Example 4: The current in a coil of self-inductance 2H is increasing according to $I=2\sin \left(t^2\right)A$. The amount of energy spent during the period when the current changes from 0 to 2 A is__________ J.

1)4

2)5

3)3

4)7

Solution:

$$\begin{array}{rl}& \mathrm{e}=\left|\mathrm{L}\left(\frac{\mathrm{di}}{\mathrm{dt}}\right)\right|=2\times 2[\cos \left({\mathrm{t}}^2\right)]2\mathrm{t}\\ & \mathrm{e}=8[\cos \left({\mathrm{t}}^2\right)]\mathrm{t}\end{array}$$

Energy $\mathrm{dU}=$ eidt
$\mathrm{dU}=16\mathrm{t}\sin \left({\mathrm{t}}^2\right)\cos \left({\mathrm{t}}^2\right)\mathrm{dt}$
$dU=8t\sin \left(2t^2\right)dt$
When
$$\begin{array}{cc}\text{Put},2t^2=x& I=0,t^2=0\\ 4tdt=dx& x=0\\ \int dU={\int }_0^{\pi }2\sin (x)dx& I=2,t^2=\frac{\pi }{2}\\ & x=\pi \end{array}$$
$$\begin{array}{rl}\mathrm{U}& =2[-\cos \mathrm{x}{]}_0^{\pi }\\ & =2(-\cos \pi -(-\cos 0^{\circ }))\\ \mathrm{U}& =4\mathrm{J}\end{array}$$

Hence, the answer is the option (1).

Example 5:

Given that the peak voltage of the circuit is 200 V & rms value of the current is 20mA. Find the power consumed (in watts) by the circuit. (give the answer to 2 decimal places)

1) 2.82

2)3.46

3)2.01

4)1.82

Solution:

Power consumption
$$\begin{array}{rl}& P=v_{rms}{i}_{rms}=\frac{1}{2}{v}_0{i}_o^{\prime }\\ & \text{Power consumed}=\frac{V_o{I}_o}{2}\\ & {\mathrm{I}}_{\mathrm{rms}}=20\mathrm{mA}\\ & {\mathrm{I}}_0=\sqrt{2}{I}_{rms}\\ & \Rightarrow P=\frac{V_o}{2}\times \sqrt{2}{I}_{rms}\\ & =\frac{200}{2}\times \sqrt{2}\times 20\times {10}^{-3}\\ & \mathrm{P}=2.82\end{array}$$

Hence, the answer is the option (1).

Summary

In AC circuits, power can be classified into active, reactive, and apparent power, each representing different aspects of energy transfer and consumption. The power factor, which measures how effectively electrical power is converted into useful work, is crucial in reducing energy losses and optimizing system performance. Real-life applications, such as improving the power factor in industrial and residential settings, help reduce electricity bills and enhance the longevity of electrical equipment. This article discusses the types of power in AC circuits, their calculation, and the importance of the power factor in practical applications.